2.3.2.1　一阶系统的结构行为

系统动力学是在时域中，采用状态空间法描述系统结构，进而分析和研究系统。系统向量形式的状态方程为：

X=f（X，U，t），X∈Rm，U∈Rr

其中，R为欧式空间；向量X为m维，U为r维。

对于一阶定常自由系统，m=0，r=0的时不变系统，则有：

dx/dt=f（x）=a0+a1x+a2x3+…

如果等式右端保留一次项和常数项，上式变为：

dx/dt=f（x）=a0+a1x

其原函数为：

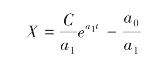
其中，C为常数。

可见，当a1＞0时，系统呈指数增长特征。自然界中，动植物在无约束的条件下表现为此种指数特性。当a1＜0时，系统呈指数减少。自然界中，放射性射线强度的衰减，被照杀或药杀的细菌消亡过程，死亡速率大于出生速率人口的减少过程都表现为指数减少。

如果等式右端保留二次项、一次项和常数项，dx/dt=f（x）=a0+a1x+a2x3+…变为：

dx/dt=f（x）=a0+a1x+a2x2

其原函数为：

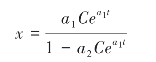
其中，C为常数。

可见，a1＞0，a2＞0，t→∞，x趋于定值，此时系统呈“S”形增长特性。

综上所述，对于一阶系统，无论控制作用多么复杂，系统或者呈指数增加，或者呈指数衰减，或者呈现渐进增长，趋于某个既定的目标出现平衡，一旦出现平衡，平衡将永远保持下去。因此一阶系统不会发生超调，更不会发生振荡。

2.3.2.2　二阶系统的结构行为

二阶系统比一阶系统更为复杂，一般在一个系统中包含两个独立的状态变量，并且这两个状态变量在同一个回路中。系统动力学用状态空间法在时域中表述系统的结构和研究系统的功能与行为。系统向量形式的状态方程如下：

X=f（X，U，t），X∈Rm，U∈Rr其中，R为欧氏空间。(www.daowen.com)

为了简化叙述，这里以二阶定常自由系统为例说明二阶系统的描述问题，这时系统为m=2，r=0的时不变系统，其向量方程可表示为：

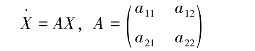
其中，X·表示dx/dt组成的列向量；A为状态转移矩阵。对于这个向量方程，可以从数学角度进行分析，研究其行为特性。下面以库存系统为例，对二阶系统的行为特性进行分析（如图2.5）。

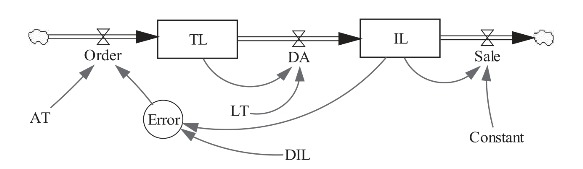
图2.5　二阶库存系统存量流量图

在上述库存系统中，如果有在途库存，系统就从一阶系统变为二阶系统。之所以成其为二阶系统，因为在系统的最大回路中包含两个水平变量TL和IL。其中，IL为实际库存量，TL为在途库存量，LT为平均订货提前期，Constant为常量，其他变量同一阶库存系统相同。

这里为了便于分析，假设Constant=0，该系统的数学描述为：

将上式对t求导，并整理得：

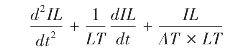
可见上式为二阶线性非奇次微分方程，其特征方程为：

该特征方程有两个根r1和r2的取值，可得对于你干的齐次方程的通解如下：

①r1≠r2时，IL=c1er1t+c2er2t；

②r1=r2=r时，IL=（c1+c2t）en；

③r=α+βi时，IL=［c1cos（βt）+c2sin（βt）］eat。

从奇次方程的通解来看，二阶库存系统的行为要比一阶系统复杂得多，不但可能出现超调，也可能出现振荡现象。

系统的行为特性同特征方程的变化有关，即同库存偏差调节时间与订货提前期的相对取值有关。即

①AT＞4IT，特征方程有两个不等实根r1和r2，r1≠r2，库存的变化规律如式①所示；

②AT=4IT，特征方程有两个相等的实根r1=r2=r，库存的变化规律如式②所示；

③AT＜4IT，特征方程有两个虚根r=α+βi，库存的变化规律如式③所示。

在此只是考虑了一个简单的线性系统，并且对于这样一个简单的线性系统也只分析了其对应的奇次方程解的情况。可见，在二阶系统中，由于库存调节时间AT和订货提前期LT的比例关系不同，系统地行为特征也不同，如何控制订货使得库存达到所期望的目标与一阶系统相比变得复杂得多。