回归分析是指对具有相关关系的多个变量，构造一个适当的数学模型（称为回归方程），将变量之间的关系表达出来，进而通过一个或多个自变量的取值来预测因变量的值。

进行回归分析时，首先，确定出因变量和自变量。被预测或被解释的变量作为因变量，用y表示；用来预测或解释因变量的一个或多个变量作为自变量，用x表示。其次，设法找出合适的数学方程（即回归方程）来描述变量之间的关系。再次，对回归方程进行统计检验。最后，统计检验通过后，可以利用回归方程，根据自变量估计、预测因变量。

当回归中只有一个自变量时称为一元回归，若y和x之间为线性关系时称为一元线性回归；当回归中有多个自变量时称为多元回归。

一元线性回归方程的形式为：y=a+bx，其中a和b是待估计的回归方程系数，a是估计的回归直线在y轴上的截距；b是回归直线的斜率，也称为回归系数。

在Excel2013中，进行回归分析时，可以使用趋势线、回归函数、回归分析工具3种回归分析方法进行回归分析。

1.使用趋势线进行回归分析

使用趋势线进行回归分析时，首先对所选的两个变量对应的样本数据绘制出一个散点图，然后在散点图的基础上添加趋势线，得到一元线性回归分析的结果。

例6-23　根据例6-20的销售收入与广告费用数据表，以销售收入为自变量，广告费用为因变量，进行一元线性回归分析。

具体操作步骤如下。

（1）绘制散点图。按照例6-20中的操作步骤，绘制出散点图，参见图1-6-46。

（2）添加趋势线。将光标定位到散点图中的点，单击鼠标右键，在弹出的快捷菜单中，选择“添加趋势线”，打开“设置趋势线格式”窗格，设置“趋势线选项”为“线性”，并单击选中“显示公式（E）”“显示R平方值（R）”复选按钮；还可以根据需要设置趋势线的其他格式。设置好格式后得到一元线性回归直线和一元线性回归方程，如图1-6-52所示。

图1-6-52　回归直线

图1-6-52中，“y＝0.0802x-7.9342”为一元线性回归方程；“R2=0.9893”为相关系数R的平方，其值越大，回归方程解释数据的能力越强，说明回归方程能够解释98.93%左右的数据，表明整体的拟合效果很好。

2.利用回归函数进行回归分析

设一元线性回归方程为y＝ax+b，利用回归函数进行一元线性回归分析时，需要使用SLOPE函数、INTERCEPT函数计算a、b的值。

INTERCEPT函数的语法为“INTERCEPT（know_y's，know_x's）”，其功能是求线性回归拟合线方程的截距b的值。其中，参数know_x's是自变量的数值区域，参数know_y's是因变量的数值区域。

SLOPE函数的语法为“SLOPE（know_y's，know_x's）”，其功能是求线性回归拟合线方程的斜率a的值。其中，参数know_x's是自变量的数值区域，参数know_y's是因变量的数值区域。

例6-24　对例6-20的销售收入与广告费用数据表，以销售收入为自变量，广告费用为因变量，使用回归函数进行一元线性回归分析。

使用回归函数进行一元线性回归分析，首先利用INTERCEPT函数和SLOPE函数分别计算出截距b、斜率a。具体操作步骤如下。(www.daowen.com)

（1）计算截距b。在E2单元格输入公式“＝INTERCEPT（B2：B16，A2：A16）”，按Enter键，得到结果“-7.934215”。

（2）计算斜率a。在E3单元格输入公式“＝SLOPE（B2：B16，A2：A16）”，按Enter键，得到结果“0.080229”，如图1-6-53所示。

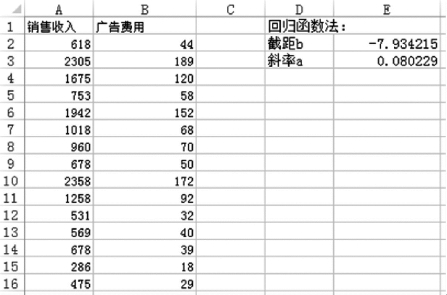
图1-6-53　利用回归函数计算的结果

根据以上计算结果，得到销售收入与广告费用之间的一元线性回归拟合线方程为“广告费用＝0.080229×销售收入-7.934215”。

3.使用回归分析工具进行回归分析

例6-25　根据例6-20中的销售收入与广告费用数据表，以销售收入为自变量，广告费用为因变量，使用回归分析工具进行一元线性回归分析。

具体操作步骤如下。

（1）建立回归方程：广告费用＝a+b×销售收入。

（2）单击“数据”选项卡下“分析”组中的“数据分析”按钮，打开“数据分析”对话框，在“分析工具”列表框中选择“回归”，单击“确定”按钮，打开“回归”对话框，如图1-6-53所示。

（3）在“回归”对话框中，按照图1-6-54设置各项参数，然后单击“确定”按钮，得到回归分析结果，如图1-6-55所示。

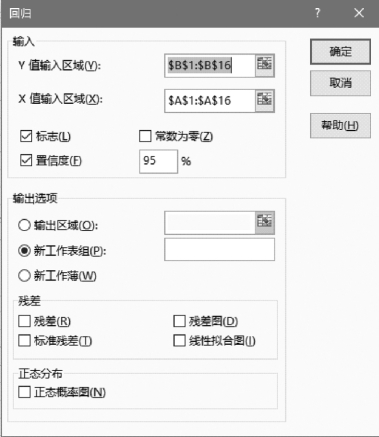
图1-6-54　“回归”对话框

（4）分析回归分析结果。如图1-6-55所示，回归分析结果分为三个部分。“回归统计”部分，“MultipleR”为“0.9946524”，表示相关系数；“RSquare”为“0.9893333”，表示相关系数的平方，写为R2；“AdjustedRSquare”为“0.9885128”，表示调整后的判定系数，其值接近1，说明回归结果的拟合程度很好。

“方差分析”部分是回归方程整体的显著性检验结果，该方差分析的原假设是自变量对因变量没有显著影响（即所有回归系数为0）。F为检验统计量；“SignificanceF”通常称为P值，是一个概率，使用者通常根据P值作出决策。决策依据是：若SignificanceF＜α，则拒绝原假设；若SignificanceF≥α，则接受原假设。本例中，SignificanceF＜α，应拒绝原假设，表明回归方程中自变量“销售收入”对因变量“广告费用”有显著影响。

第三部分列出了回归的系数以及置信区间。可知，Intercept是截距a，值为“-7.934215”；“销售收入”是斜率b，值为“0.0802293”，因此一元线性回归方程可写为：广告费用＝-7.934215+0.0802293×销售收入。“tStat”列是回归系数检验统计量，“P-value”列是P值，“Lower95%”和“Upper95%”列是置信区间的下限和上限。

图1-6-55　回归分析结果

由上述三种方法的计算结果可知，三种方法计算出的一元线性回归拟合线方程都是相同的。其中，使用趋势线进行回归分析最简单、直观；使用回归函数，关键是理解好SLOPE函数和INTERCEPT函数的含义，以及其参数的含义；使用回归分析工具进行回归分析得到的结果包含更多的信息量。