相关分析是研究变量之间的相关关系。相关关系是指变量之间保持着某种不确定的依存关系，但这种关系不是一一对应的。在相关关系中，一个变量的取值不能由另一个变量唯一确定。给定一个变量的值，而另一个变量的取值在一定范围内变动，且这种变化是受随机因素影响的。例如，一个人的收入水平（y）与受教育程度（x）的关系，收入水平与受教育程度有关系，但受教育程度不是决定收入的唯一因素，收入还受职业、工作年限等多种因素的影响。因此，相关关系是一种非确定性的关系。

1.相关关系的分类

（1）按相关程度划分，相关关系分为完全相关、不相关和不完全相关。

当一个变量的变化完全由另一个变量的变化所决定时，称这两个变量间的关系为完全相关；当两个变量彼此互相不影响，其发生的变化各自独立时，就称这两个变量不相关；而当两个变量之间的关系介于完全相关和不相关之间时，就称这两个变量不完全相关。完全相关可以用函数来表示；不完全相关是相关分析的主要研究对象。

（2）按相关的方向划分，相关关系分为正相关和负相关。

正相关是指相关变量之间的变化趋势相同，即当自变量的值增加时，因变量的值也随之发生相应的增加；当自变量的值减少时，因变量的值也随之发生相应的减少。例如，商品的批发价与销售价之间的关系是正相关的。

负相关是指相关变量之间的变化趋势相反，即当自变量的值增加时，因变量的值随之发生相应的减少；而当自变量的值减少时，因变量的值则随之发生相应的增加。例如，汽车的行驶速度与所用时间之间的关系是负相关的。

（3）按相关形式划分，相关关系分为线性相关和非线性相关。

当两种相关变量的数量之间大致呈现出线性关系时，称为线性相关。当两种变量之间近似表现为一条曲线时，则称为非线性相关。

（4）按影响因素的多少来看，相关关系可分为单相关、复相关和偏相关。

单相关是指两个变量之间的相关关系，即一个因变量对一个自变量的相关关系，也叫简单相关。

复相关是指三个或三个以上变量之间的相关关系，即一个因变量对两个或两个以上的多个自变量的相关关系，又称多元相关。

偏相关是指某一变量与多个变量相关时，假定其他变量不变，其中两个变量的相关关系。

2.简单相关分析的方法

简单相关分析是指对两个变量之间的相关关系进行分析，即通过计算两个变量之间的相关系数，对两个变量之间是否显著相关作出判断。简单相关分析的方法主要有散点图和相关系数。

（1）散点图。散点图用X轴和Y轴分别表示不同的变量，两个变量之间对应的变量值用坐标点描绘。根据散点图的形状可以直观地判断出两个变量之间存在何种相关关系。

例6-20　某公司为了研究销售收入与广告费用支出之间的关系，随机抽取15家分公司的数据，得到销售收入和广告费用支出的数据表（单位：万元），如图1-6-45所示。用散点图描绘销售收入和广告费用支出之间的关系。

具体操作步骤为：选择A1：B16单元格区域，然后单击“插入”选项卡下“图表”组中的“插入散点图（X、Y）或气泡图”下拉按钮选择列表中的第一个散点图样式，生成散点图；再根据需要，添加横坐标、纵坐标标题，如图1-6-46所示。

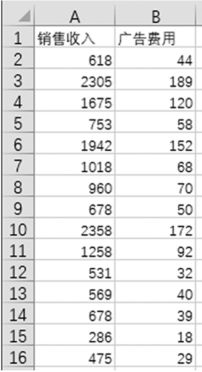
图1-6-45　销售收入和广告费用

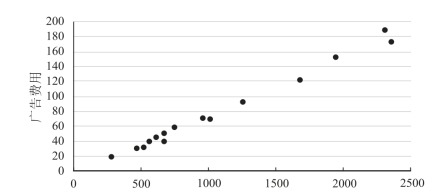
图1-6-46　散点图

（2）相关系数。散点图只能大体上反映变量之间的相关关系，但对变量之间相关关系的密切程度描述得不够精确。为了精确地反映相关关系的密切程度，还需要计算相关系数。

计算相关系数的方法有多种，最简单的一种称为积差法。用积差法计算相关系数的公式如下。

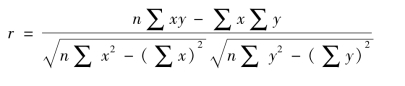
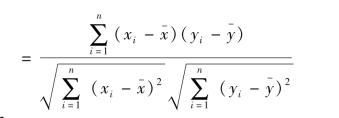
相关系数r有下列性质。

①-1≤r≤1，r的绝对值越大，表明两个变量之间的相关程度越强。

②当0＜r≤1时，表明两个变量之间存在正相关关系。当r＝1时，表明两个变量之间存在完全正相关的关系。

③当-1≤r＜0时，表明两个变量之间存在负相关关系。当r＝-1时，表明两个变量之间存在完全负相关的关系。(www.daowen.com)

④当r＝0时，表明两个变量之间没有线性相关关系。

在Excel2013中，如果计算两个变量之间的相关系数，可以使用CORREL函数；如果计算多个变量之间的相关系数，可以用数据分析工具的“相关系数”功能来计算。

CORREL函数返回两个变量之间的相关系数，其语法为“CORREL（Array1，Array2）”，用于返回单元格区域Array1和Array2之间的相关系数。参数Array1为第一组数值单元格区域，参数Array2为第二组数值单元格区域。

例6-21　利用例6-20的销售收入和广告费用数据，计算两者之间的相关系数。

（1）第一种方法：用CORREL函数计算相关系数。

具体操作步骤如下。

①单击B18单元格，单击“插入函数”按钮fx，打开“插入函数”对话框，在“搜索函数”输入框中输入“CORREL”，按“Enter”键，“选择函数”列表框中显示“CORREL”，选中该函数，单击“确定”按钮，打开“函数参数”对话框，如图1-6-47所示。

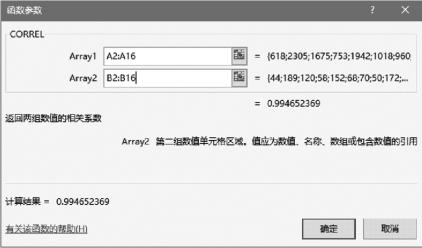
图1-6-47　CORREL函数参数对话框

②在“函数参数”对话框中，设置“Array1”框中的区域为A2：A16单元格区域，“Array2”框中的区域为B2：B16单元格区域，单击“确定”按钮。这样在B18单元格添加了公式“＝CORREL（A2：A16，B2：B16）”，计算结果为“0.9946524”，该数就是相关系数，如图1-6-48所示。

（2）第二种方法：用数据分析工具的“相关系数”功能来计算相关系数。

具体操作步骤如下。

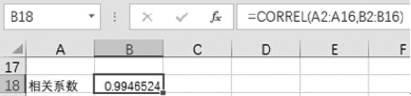
图1-6-48　相关系数计算结果

①单击“数据”选项下“分析”组中的“数据分析”按钮，打开“数据分析”对话框，在“分析工具”列表框中选择“相关系数”，单击“确定”按钮，打开“相关系数”对话框，如图1-6-48所示。

②在“相关系数”对话框中，如图1-6-49所示，设置“输入区域”为A1：B16单元格区域，单击选中“标志位于第一行”复选按钮，单击选中“输出区域（O）”单选按钮，并设置A20单元格作为输出区域，然后单击“确定”按钮，得到相关系数的计算结果，如图1-6-50所示。

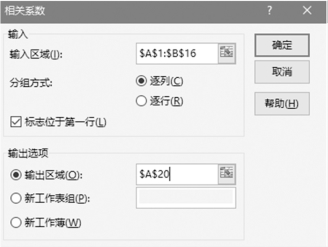
图1-6-49　“相关系数”对话框

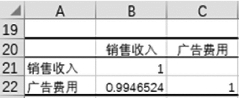
图1-6-50　相关系数计算结果

3.相关系数的检验

相关系数是根据样本数据计算出来的两个不相关的变量，其样本相关系数也可能较高。所以，要从样本相关系数判断总体是否具有相同的相关关系，就需要对相关系数进行统计检验，其检验过程如下。

第1步，提出原假设H0：r=0；备择假设H1：r≠0。

第2步，构造相关系数统计量为t：，该统计量的自由度为n-2。

第3步，给定一个小概率（显著水平）α，计算临界值tα（n-2）。

第4步，作出决策。若，则拒绝原假设H0，表明两个变量之间线性相关关系显著；若，则接受原假设H0，表明两个变量之间线性相关关系不显著。

例6-22　对例6-21中计算的相关系数进行检验（设α＝0.05）。

具体操作步骤为：在B25单元格输入显著水平值“0.05”；在B26单元格输入公式“＝B18*SQRT（COUNT（A2：A16）-2）/SQRT（1-B182）”，计算t统计量；在B27单元格输入公式“＝TINV（B25，COUNT（A2：A16）-2）”，计算t临界值；在B28单元格输入公式“＝IF（B26＞B27，＂线性相关关系显著＂，＂无显著的线性相关关系＂）”，得到相关系数的检验结果，如图1-6-51所示。从结果中看出，销售收入和广告费用之间相关关系是显著的。

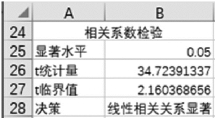
图1-6-51　相关系数检验结果