当方差分析中只涉及一个因素时，称为单因素方差分析。例6-16要检验的是不同位置超市的销售额平均值是否相等，只涉及一个因素“超市位置”，它是自变量，销售额是因变量。因此，该问题属于单因素方差分析。

单因素方差分析可以用Excel2013中数据分析功能的“方差分析：单因素方差分析”模块来完成计算，然后根据计算结果进行分析，作为决策。若F＞Fα，则拒绝原假设H0，表明自变量对因变量有显著影响；否则不能拒绝原假设H0。

所以在例6-16中，置信水平为5%，进行方差分析的具体操作步骤如下。

（1）提出假设。

H0：μ1=μ2=μ3，即三种不同位置超市的平均销售额相等。

H1：μ1，μ2，μ3不全相等，即超市位置对销售额有显著差异和影响。

（2）单击“数据”选项卡下“分析”组中的“数据分析”按钮，打开“数据分析”对话框，在“分析工具”列表框中选择“方差分析：单因素方差分析”，单击“确定”按钮后打开“方差分析：单因素方差分析”对话框，如图1-6-37所示。在对话框中按图1-6-37设置各个参数，完成后单击“确定”按钮，得到计算结果，如图1-6-38所示。(www.daowen.com)

（3）分析结果，作出决策。计算结果中，21～26行是方差分析表的结果，各列含义为：“SS”表示误差平方和，“df”表示自由度，“MS”表示均方差，“F”表示F检验统计量，“P-value”表示概率，是用于检验的P值，“Fcrit”表示给定显著水平α下的临界值Fα。

从方差分析结果可以看到，F=7.1195484，Fα=3.5218933，有F＞Fα，所以拒绝原假设H0，即μ1=μ2=μ3不成立。也就是说超市位置对销售额的均值影响是显著的。

在决策时，也可以用P值进行决策。若P＜α，则拒绝原假设H0，否则不拒绝原假设。对于本例，P＝0.004926，α＝0.05，有P＜α，所以拒绝原假设H0。得出相同的决策：超市位置对销售额的均值影响是显著的。

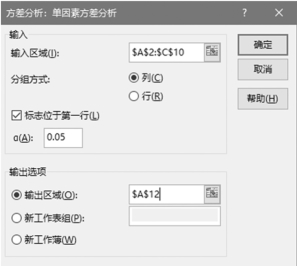
图1-6-37　“方差分析：单因素方差分析”对话框

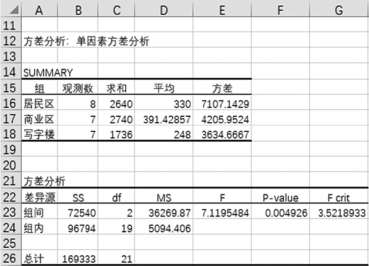
图1-6-38　单因素方差分析计算结果