1.方差分析

方差分析是检验多个总体均值是否相等的统计方法。它研究的是分类自变量对数值型因变量的影响，其目的是通过数据分析找出对事物有显著影响的因素，各因素之间的交互作用等。为了理解有关概念，先看一个例子。

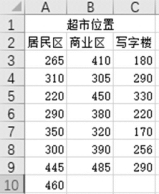
图1-6-36　超市位置和销售额

例6-17　一家连锁超市进行一项研究，想确定超市所在的位置对销售额是否有显著影响。将超市位置分为居民区、商业区、写字楼3类，并在不同位置分别随机抽取若干家超市，其中居民区抽取8家，商业区抽取7家，写字楼抽取7家，获得每家超市的年销售额数据如图1-6-36所示。现要求分析超市位置对销售额是否有显著影响。这问题归结为对3个不同位置超市的销售额平均值是否相等的判断，这就需要使用方差分析来解决。

2.因素和水平

在方差分析中，所要检验的对象称为因素或因子。因素可能取的值称为水平。例如图1-6-36中，“超市位置”是因素，它的值“居民区”“商业区”“写字楼”称为水平。

3.观测值(www.daowen.com)

每个因子水平下得到的样本数据称为观测值。例如，图1-6-36中，单元格的销售额数就是观测值。

4.方差分析中的基本假定

方差分析中有三个基本假定：每个总体服从正态分布、各个总体的方差必须相等、观测值独立。

5.方差分析的一般假设

设因素有k个水平，每个水平的均值分别用μ1，μ2，…，μk表示，要检验k个水平（总体）的均值是否相等，需要提出如下假设。

H0：μ1=μ2=…=μk，即自变量对因变量没有显著差异和影响。

H1：μ1，μ2，…，μk不全相等，即自变量对因变量有显著差异和影响。