上一小节介绍了一个总体的均值、方差的检验，本小节将介绍两个总体参数的检验，看它们是否有显著的差异。两个总体参数的检验主要有两个总体均值之差的检验、方差的检验。

1.两个总体均值之差的检验

设两个总体的均值分别为μ1，μ2，两个总体均值之差表示为μ1-μ2，其原假设和备择假设形式如下：

双侧检验中，原假设H0：μ1-μ2=0，备择假设H1：μ1-μ2≠0。

左侧检验中，原假设H0：μ1-μ2≥0，备择假设H1：μ1-μ2＜0。

右侧检验中，原假设H0：μ1-μ2≤0，备择假设H1：μ1-μ2＞0。

在Excel2013中，其数据分析功能提供了多种检验方法，用来检验两个总体均值之差，包括以下四种。

（1）z-检验：双样本平均差检验。它在已知两个总体方差的情况下，对两个总体进行双样本z检验。

（2）t-检验：双样本等方差假设。它在两个总体方差未知但相等的情况下，对两个总体平均值进行t-检验。

（3）t-检验：双样本异方差假设。它在两个总体方差未知且不相等的情况下，对两个总体平均值进行t-检验。

（4）t-检验：平均值的成对二样本分析。它可以对成对数据进行平均值之差的检验。

对于以上各双样本参数检验，决策准则可以用P值决策准则，即若检验方法计算出来的P值小于显著水平α的值，则拒绝原假设H0。

例6-15　为了比较新旧两种肥料对产量的影响，某研究机构选择了面积相同、土壤等条件相同的20块田地，分别施用新旧两种肥料，得到的产量数据如表1-6-6所示，且两个总体方差未知但相等。比较新肥料获得的平均产量是否与旧肥料获得的平均产量相等（显著水平α＝5%）。

表1-6-6　新旧肥料的产量数据

两个总体方差未知但相等情况下，双样本均值差检验的步骤如下。

（1）提出原假设H0：μ1-μ2=0，备择假设H2：μ1-μ2≠0。

（2）在表中输入数据，参见图1-6-33的A列、B列数据。

（3）单击“数据”选项卡下“分析”组中的“数据分析”按钮，打开“数据分析”对话框；在“分析工具”列表框中选择“t-检验：双样本等方差假设”，单击“确定”按钮后打开“t-检验：双样本等方差假设”对话框，如图1-6-32所示。(www.daowen.com)

（4）在“t-检验：双样本等方差假设”对话框中，设置各个参数的值。“变量1的区域（1）”设置为A2：A21单元格区域；“变量2的区域（2）”设置为B2：B21区域；“假设平均差”设置为“0”；“α（A）”设置为“0.05”；单击选中“输出区域（O）”单选按钮，并选择D2单元格作为输出结果的位置，如图1-6-32所示。单击“确定”按钮，输出计算结果，如图1-6-33所示。

（5）分析检验结果。从图1-6-33的检验结果看出，计算的t值为“-5.715917”，而P（T≤t）单尾和P（T≤t）双尾的值都远小于显著水平α值5%，说明应拒绝原假设H0。因此得出结论：施用新肥料获得的平均产量与旧肥料获得的平均产量不相等。

2.两个总体方差的检验

在总体方差未知的独立双样本的t检验中，需要事先知道两个总体的方差是否相等。这个问题可以用Excel2013的数据分析工具的“F检验：双样本方差”来进行检验。

例6-16　使用例6-15的数据，检验实施新、旧肥料获得的两个产量总体方差是否相等（显著水平α＝5%）。

双样本方差检验的操作步骤如下。

（1）提出原假设H0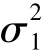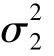：=，备择假设H1：≠。

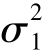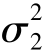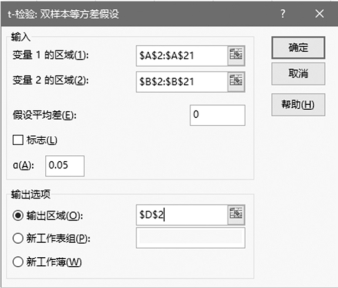
图1-6-32　“t-检验：双样本等方差假设”对话框

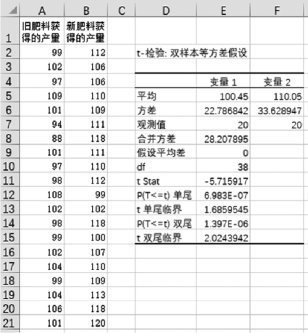
图1-6-33　例6-15的输出结果

（2）单元“数据”选项卡下“分析”组中的“数据分析”按钮，打开“数据分析”对话框；在“分析工具”列表框中选择“F检验：双样本方差”，单击“确定”按钮后打开“F检验：双样本方差”对话框，如图1-6-34所示。

（3）在“F检验：双样本方差”对话框中，设置如图1-6-34所示的各个参数，单击“确定”按钮后，得到计算结果，如图1-6-35所示。

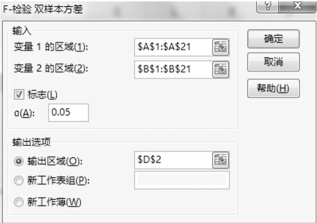
图1-6-34　“F检验：双样本方差”对话框

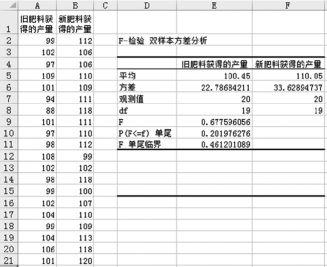
图1-6-35　例6-16的输出结果

（4）分析检验结果。本例为双侧检验，其P值是“P（F≤f）单尾”对应概率的2倍，所以P值为2*0.201976276＝0.403952552，P值明显远大于显著水平5%，说明不能拒绝原假设H0。因此得出结论：施用新肥料和旧肥料所获得的产量方差是相等的。