根据假设检验的不同内容和不同条件，需要采用不同的检验统计量。在单个总体参数的检验中，使用的检验统计量有3个：Z统计量、t统计量和x2统计量。其中，Z统计量和t统计量常用于均值的检验，x2统计量常用于方差的检验。

1.一个总体均值的假设检验

一个总体均值的检验，要考虑其方差或均值是否已知、样本量大小而选择不同的检验方法。一个总体均值的检验方法如表1-6-4所示。

表1-6-4　一个总体均值的假设检验方法

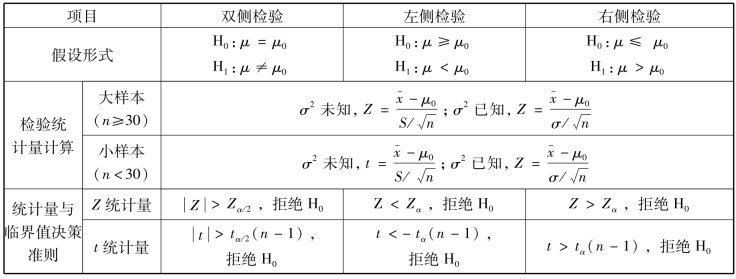
说明：在Excel中，上表中的临界值Zα用统计函数NORMSINV（1-α）来计算；tα（n-1）用统计函数TINV（α，n-1）来计算。

例6-12　某饮料厂采用自动装瓶机来灌装饮料，每瓶质量规定为500克，标准差不超过10克，每天定时检查。某天抽取16瓶，测得平均值498克，样本标准差为16.2克。假设瓶装饮料质量服从正态分布，问：取显著性水平α＝0.05时，检验该天生产的饮料质量是否符合标准？

分析：根据题目，得到μ0=500，σ=10，n=16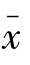=498，α=0.05。本题的检验是要证明假设“饮料质量不符合标准”，因此，应采用双侧检验。本例的实质是已知方差，用Z统计量进行计算。

具体操作步骤如下。

（1）提出原假设和备择假设，H0：μ=500；H1：μ≠500。

（2）输入样本数、样本均值、总体均值、总体标准差、显著水平的值，参见图1-6-29中B4：B8单元格区域的数据。

（3）计算Z检验的临界值。在B9单元格输入公式“＝NORMSINV（1-B8/2）”，按“Enter”键，得到临界值“1.959963985”。

（4）构造Z检验统计量，计算Z统计量值。在B10单元格输入公式“＝（B5-B6）/（B7*SQRT（B4））”，按“Enter”键。本步骤中的公式相当于计算。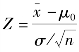

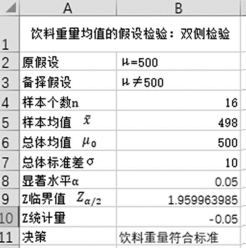
图1-6-29　例6-11的计算结果

（5）根据决策准则作出决策。在B11单元格输入公式“＝IF（ABS（B10）＞B9，＂饮料质量不符合标准＂，＂饮料质量符合标准＂）”，按“Enter”，得到决策结果“饮料质量符合标准”。本步骤中的公式相当于判断，|Z|＝0.05，Zα/2=1.959963985，所以不成立，从而不拒绝原假设H0。检验结果表明：该天生产的饮料质量是符合标准的。

例6-13　某一手机厂家声称其某种型号的手机电池在充满电的情况下待机时间可达200小时以上。为了对此进行检验，经销商随机选择了20部手机进行测试，发现平均待机时间为197小时，样本标准差为3小时。如果检验的显著性水平为5%，厂家的说法可靠吗？

分析：对于该问题，检验的原假设和备择假设为“H0：μ≥200；H1：μ＜200”。假设检验为左侧检验，方差未知，应用t检验方法进行检验。根据题目，得到μ0=200，n=20，x-=197，S=3，α=0.05。

具体操作步骤如下。

（1）提出原假设和备择假设，H0：μ≥200；H1：μ＜200。

（2）输入样本数、样本均值、样本标准差、总体均值、显著水平的值，参见图1-6-30中B4：B8单元格区域的数据。(www.daowen.com)

（3）计算t检验的临界值。在B9单元格输入公式“＝TINV（B8，B4-1）”，按“Enter”，得到临界值“2.093”。

（4）构造t检验统计量，计算t统计量值。在B10单元格输入公式“＝（B5-B7）/（B6/SQRT（B4））”，按“Enter”，得到统计量“-4.472”。本步骤中的公式相当于计算。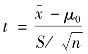

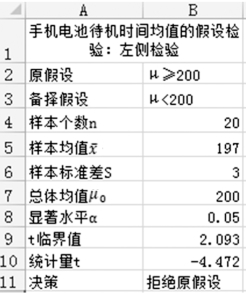
图1-6-30　例6-12的计算结果

（5）根据决策准则作出决策。在B11单元格输入公式“＝IF（B10＜-B9，＂拒绝原假设＂，＂不能拒绝原假设＂）”，按“Enter”，得到决策结果“拒绝原假设”。公式相当于判断t＜-tα（n-1），由计算结果，t＝-4.472，tαn-（）1=2.093，因此，t＜-tα（n-1）成立，从而拒绝原假设H0。检验结果表明：手机的待机时间小于200小时。

2.一个总体方差的假设检验

总体方差的检验使用卡方（χ2）分布。总体方差的检验，不论样本容量斜值的大小，都要求总体服从正态分布。用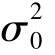表示假定的总体方差的某一取值，一个总体方差的假设检验分为三种形式，各种形式的检验方法如表1-6-5所示。

表1-6-5　一个总体方差的假设检验方法

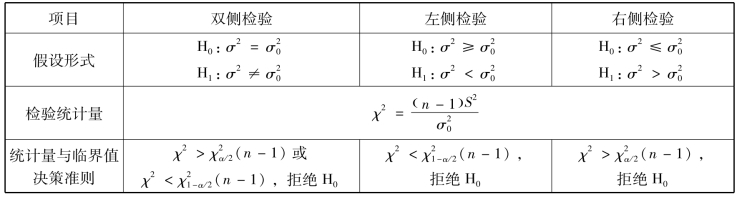
说明：卡方检验临界值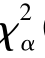（n-1）可用Excel统计函数CHIINV（α，n-1）计算。

例6-14　某饮料厂采用自动装瓶机来灌装饮料，每瓶质量规定为500克，标准差不超过10克，每天定时检查。某天抽取16瓶，测得平均质量为498克，样本标准差为16.2克。假设瓶装饮料质量服从正态分布，问：取显著性水平α＝0.05时，检验该天生产的饮料质量标准差是否符合标准？

具体操作步骤如下。

（1）提出原假设和备择假设，H0：σ2≤102；H1：σ2＞102。

（2）输入样本个数、样本均值、样本标准差、总体标准差、显著水平的值，参见图1-6-31中B4：B8单元格区域的数据。

（3）计算卡方（χ2）检验的临界值。在B9单元格输入公式“＝CHIINV（B8/2，B4-1）”，按“Enter”，得到临界值“27.448”。

（4）构造χ2检验统计量，计算χ2值。在B10单元格输入公式“＝（B4-1）*B6＾2/B7＾2”，按“Enter”，得到结果“39.366”。本步骤中的公式相当于计算。

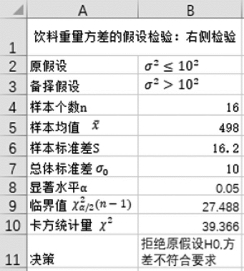
图1-6-31　下列6-13的计算结果

（5）根据决策准则作出决策。在B11单元格输入公式“＝IF（B10＞B9，＂拒绝原假设H0，方差不符合要求＂，＂接受原假设H0，方差符合要求＂）”，按“Enter”，得到决策结果“拒绝原假设H0，方差不符合要求”。据此检验结果表明：该天生产的饮料质量标准差不符合标准。

综合例6-11和例6-13的结果，得出结论：该饮料厂生产瓶装饮料质量符合规定，但不稳定。