对总体均值进行区间估计时，分为以下三种情况。

1.总体方差已知情况下总体均值的区间估计

总体服从正态分布，且方差已知，或者非正态分布总体、大样本、方差已知的情况下，总体均值的置信区间的计算公式为“”。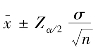

其中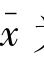，为样本均值，n为样本容量，σ为已知的总体标准差，α是事先确定的总体均值不包含在置信区间的概率，1-α称为置信水平，Zα/2为正态分布临界值。

2.总体方差未知且为大样本（样本数≥30）情况下总体均值的区间估计

这种情况下，不管总体是否为正态分布，总体均值的置信区间的公式为“”。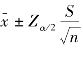

其中，S为样本标准差，其他参数含义同上述第1种情况。

在Excel中，标准差用STDEV函数计算，Zα/2用正态分布的累积分布的反函数NORMSINV计算。

3.总体方差未知且为小样本情况下总体均值的区间估计

总体为正态分布、方差未知时，均值的置信区间公式为“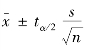”。其中，tα/2是自由度为n-1时t分布中右侧面积为α/2的t值，该值用Excel的TINV函数计算，其语法为TINV（α，df），其中，参数α表示双尾t分布的概率，参数df表示样本的自由度。

说明：有关正态分布、t分布的知识，可参考概率论与数理统计、统计学等相关书籍的内容。

例6-10　假设GDP增长率服从正态分布，利用例6-8抽取的20个地区GDP增长率数据，分两种情况，估计全国GDP平均增长率的置信区间：①设已知GDP增长率方差为24，估计在置信水平95%下全国GDP平均增长率的置信区间；②设总体方差未知，估计在置信水平95%下全国GDP平均增长率的置信区间。

（1）已知方差为24，计算全国GDP平均增长率的置信区间。具体操作步骤如下。

①建立如图1-6-22所示的区间估计计算表（不含D列、F列的数据）。

②在D4单元格输入方差值“24”；在D6单元格输入置信水平值“95%”。(www.daowen.com)

③在D2单元格输入公式“＝COUNT（A2：A21）”，计算样本个数；在D3单元格输入公式“＝AVERAGE（A2：A21）”，计算样本均值；在D5单元格输入公式“＝SQRT（D4）”，计算总体标准差；在D7单元格输入公式“＝ABS（NORMSINV（（1-D6）/2））”，计算Z值；在D8单元格输入公式“＝D3-D7*D5/SQRT（D2）”，计算置信区间下限；在D9单元格输入公式“＝D3+D7*D5/SQRT（D2）”，计算置信区间上限。计算结果如图1-6-22的D列数据。

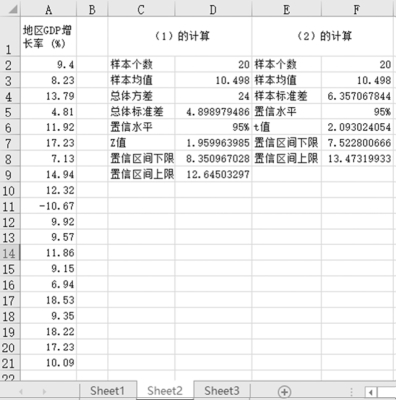
图1-6-22　GDP增长率数据和置信区间的计算结果

经过以上步骤后，得到方差为24时，在置信水平95%下全国GDP平均增长率的置信区间为［8.35，12.65］。

（2）方差未知且为小样本时，计算全国GDP平均增长率的置信区间。具体操作步骤如下。

①在F5单元格输入置信水平值“95%”。

②在F2单元格输入公式“＝COUNT（A2：A21）”，计算样本个数；在F3单元格输入公式“＝AVERAGE（A2：A21）”，计算样本均值；在F4单元格输入公式“＝STDEV（A2：A21）”，计算样本标准差；在F6单元格输入公式“＝TINV（1-F5，F2-1）”，计算t值；在F7单元格输入公式“＝F3-F6*F4/SQRT（F2）”，计算置信区间下限；在F8单元格输入公式“＝F3+F6*F4/SQRT（F2）”，计算置信区间上限。计算结果如图1-6-22的F列数据。

经过以上步骤后，方差未知且为小样本时，在置信水平95%下全国GDP平均增长率的置信区间为［7.52，13.47］。

对于第②个问题，还可以用Excel的“数据分析”工具的描述统计模块进行GDP平均增长率的区间估计。具体操作方法为：在“描述统计”对话框中单击选中“平均数置信度”复选按钮，并输入置信度“95”，如图1-6-23所示。单击“确定”按钮后，输出结果包含如图1-6-24所示的信息。

根据图1-6-24的“平均”“置信度（95.0%）”两项指标值，得到GDP平均增长率在置信水平95%下的置信区间为10.498±2.9752，即［7.5228，13.4732］。

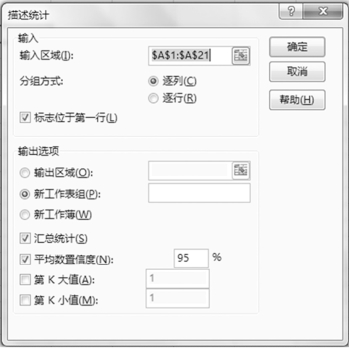
图1-6-23　“描述统计”对话框设置

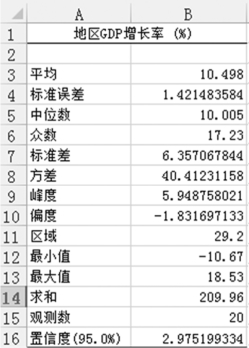
图1-6-24　描述统计的输出结果