2004年—2017年北京市教育业的增加值、固定资产投资额、从业人员数见表5-27：

表5-27 2004年—2017年北京市教育业情况

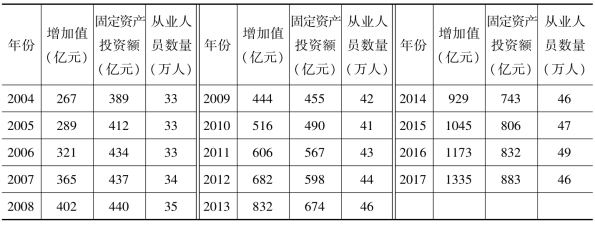
5.4.5.1 增加值的预测

对北京市教育业增加值的预测运用时间序列指数回归模型和GM（1，1）模型相结合的方法。

（1）时间序列指数回归模型

根据历史数据，得到北京市教育业增加值的指数回归模型为：

y=219.2·e0.128x，R2=0.995

拟合效果很好，相对误差绝对值平均为2.9%，精度很高。

（2）GM（1，1）模型

同样根据历史数据，得到北京市教育业增加值的GM（1，1）模型白化方程的时间响应式为：

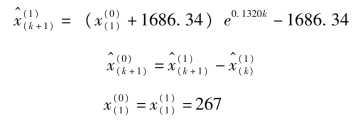
相对误差绝对值平均为2.2%<10%，通过检验。

（3）综合加权平均模型

运用以下模型计算预测最终结果：

x=0.5·（x1+x2）

其中，x1为GM（1，1）模型的预测值，x2为时间序列指数回归模型的预测值。

由此得表5-27、图5-18。

表5-27 北京市教育业增加值的预测

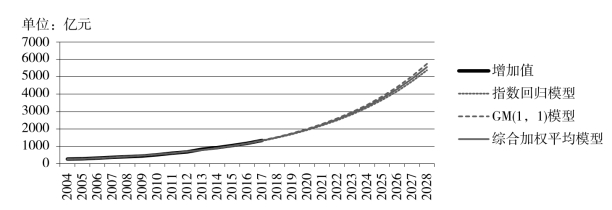
图5-18 北京市教育业增加值的趋势预测

5.4.5.2 所需固定资产投资额的预测

对北京市教育业所需固定资产投资额的预测运用时间序列指数回归模型和GM（1，1）模型相结合的方法。

（1）时间序列指数回归模型

根据历史数据，得到北京市教育业固定资产投资额的指数回归模型为：

y=337.3·e0.067x，R2=0.956

拟合效果很好，相对误差绝对值平均为5.1%，精度较高。

（2）GM（1，1）模型

同样根据历史数据，得到北京市教育业固定资产投资额的GM（1，1）模型白化方程的时间响应式为：(www.daowen.com)

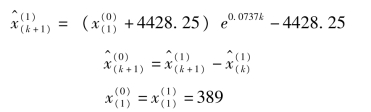
相对误差绝对值平均为4.2%<10%，通过检验。

（3）综合加权平均模型

运用以下模型计算预测最终结果：

x=0.5·（x1+x2）

其中，x1为GM（1，1）模型的预测值，x2为时间序列指数回归模型的预测值。

由此得表5-28、图5-19。

表5-28 北京市教育业所需固定资产投资额的预测

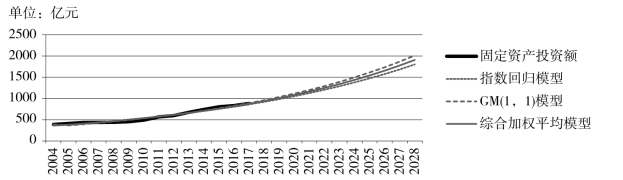
图5-19 北京市教育业所需固定资产投资额的趋势预测

5.4.5.3 所需人才的预测

对北京市教育业所需人才的预测运用时间序列线性回归模型和GM（1，1）模型相结合的方法。

（1）时间序列线性回归模型

根据历史数据，得到北京市教育业从业人员数量的指数回归模型为：

y=1.368x+30.53，R2=0.911

拟合效果较好，相对误差绝对值平均为3.6%，精度较高。

（2）GM（1，1）模型

同样根据历史数据，得到北京市教育业从业人员数量的GM（1，1）模型白化方程的时间响应式为：

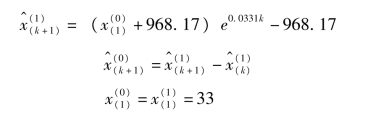
相对误差绝对值平均为3.8%<10%，通过检验。

（3）综合加权平均模型

运用以下模型计算预测最终结果：

x=0.5·（x1+x2）

其中，x1为GM（1，1）模型的预测值，x2为时间序列线性回归模型的预测值。

由此得表5-29、图5-20。

表5-28 北京市教育业所需人才数量的预测

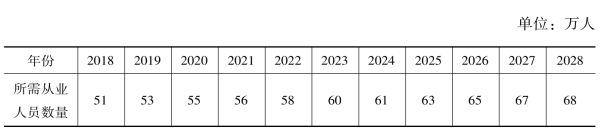
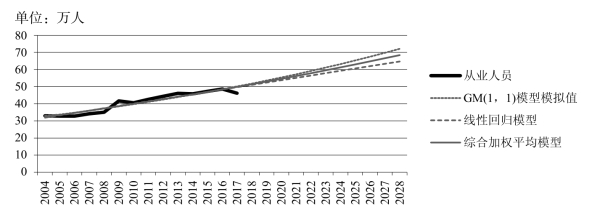
图5-20 北京市教育业所需人才数量的趋势预测