对于北京市KISI增加值的预测,我们将采用Markov生命周期演化模型。
5.1.2.1 北京市KISI的Logistic生命周期演化模型预测
根据第二章的北京市KISI的Logistic生命周期演化模型:
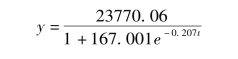
可得模型的相对误差绝对值平均为2.84%(见表5-1),精度很高,但是2017年的误差为-4.4%,且近3年的误差进一步扩大,并且都为负值。为进一步提高拟合精度,我们采用Markov随机过程方法对模型误差进行处理。
表5-1 北京市KISI增加值模型模拟与实际的对比
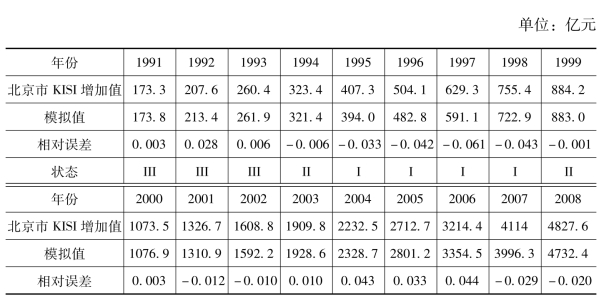
续表
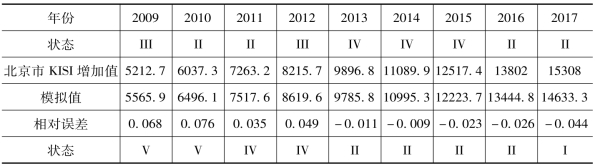
数据来源:《北京市统计年鉴(1992—2018)》
5.1.2.2 预测结果的M arkov 精细化
(1)状态的划分
将相对误差ε(k)划分为m个状态,如果
![]()
则表明第k年的相对误差处于第i种状态,a1i和a2i分别表示第i种状态的下界和上界。
(2)状态转移概率矩阵的构造
令w步转移概率为![]() ,记:
,记:
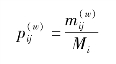
其中:![]() 为状态Ei经过w步转移达到状态Ej的次数;Mi为Ei出现的次数。
为状态Ei经过w步转移达到状态Ej的次数;Mi为Ei出现的次数。
由w步转移概率元素![]() 构成的矩阵称为w步转移概率矩阵,记为:
构成的矩阵称为w步转移概率矩阵,记为:

已知转移矩阵R(w)和初始状态Ei,则马尔柯夫链可以确定。
(3)预测值的计算
选取离预测年最近的j个年份,以这几年的相对误差所对应的状态为初始状态Ei,按离预测年由近到远,转移步数分别为1,2,…,j,在转移步数对应的转移矩阵R(w)中,取起始状态所对应的行向量
![]() (www.daowen.com)
(www.daowen.com)
从而组成新的概率矩阵
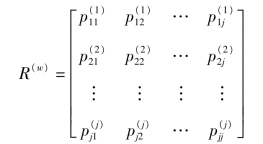
取
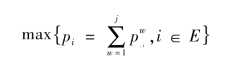
所对应的状态为预测年份的状态,则该年度的预测值为:
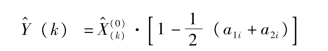
对于后续年份预测,将前一年预测的状态计入数据序列重新构置马尔柯夫链,重复运用此方法进行逐年预测,直到预测年为止。
5.1.2.3 马尔柯夫链模型的拟合精度预测
(1)状态划分
由表5-1 可以看出,1991年—2017年27年间的相对误差分散在-6.1%~7.6%之间,根据各个状态的年份数量要大致均衡、区间要大致匀称的原则,相对误差分散的地方状态区间应划分得大一些,相对误差集中的地方状态区间应划分得小一些的原则,我们将北京市KISI的生命周期模型拟合值情况划分为5 种状态,其状态划分标准见表5-2。
表5-2 北京市KISI生命周期模型拟合精度指标状态划分表

(2)构造转移概率矩阵
根据状态划分表确定出1991年—2017年各年的状态(见表5-1),同时可得4 步内的转移概率矩阵为:

(3)利用转移概率矩阵,组成要预测年份的新转移概率矩阵
选择离预测年最近的4 个年份,转移步数分别定为1,2,3,4。如预测2018年的概率矩阵为:
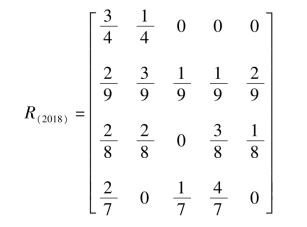
则2018年的KISI将处于第I种状态;将上年的预测状态计入数据序列重新构置马尔柯夫链,分别得到2019年—2030 的概率矩阵,通过计算,知道它们都将处于第I种状态。
5.1.2.4 预测结果
运用上述方法,得到1991年—2017年Markov生命周期模型的模拟值及其相对误差,结果显示,相对误差绝对值平均值为0.8%,精度有了显著的提高。据此模型对北京市2018年—2031年KISI增加值的预测结果见表5-3,其发展趋势见图5-1。
表5-3 北京市KISI增加值的Markov 生命周期模型预测结果
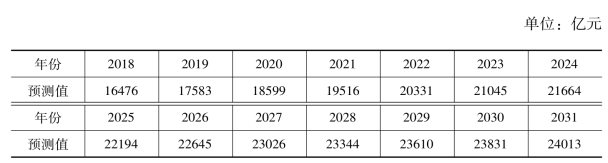
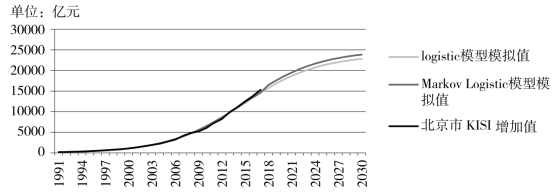
图5-1 北京市KISI增加值的趋势预测
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。







