当无功功率参与市场报价时,市场拍卖人的决策模型同样如式(5.13)~式(5.18)所示。写成如下松弛的形式,目标函数为:
满足约束:
满足约束:
其中的符号含义如前所述。当拉格朗日乘子αpk,αqk,λl,φ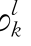 ,φ
,φ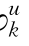 等取值合理时,上述问题与式(5.13)~式(5.18)所示的决策模型是等价的。
等取值合理时,上述问题与式(5.13)~式(5.18)所示的决策模型是等价的。
类似于有功网损的泰勒展开公式,将网络无功损耗QL按照发电机节点注入无功功率进行泰勒展开,得到:
其中的符号含义如前所述。当拉格朗日乘子αpk,αqk,λl,φ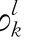 ,φ
,φ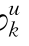 等取值合理时,上述问题与式(5.13)~式(5.18)所示的决策模型是等价的。
等取值合理时,上述问题与式(5.13)~式(5.18)所示的决策模型是等价的。
类似于有功网损的泰勒展开公式,将网络无功损耗QL按照发电机节点注入无功功率进行泰勒展开,得到:
式中:Δ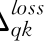 (qk)为泰勒展开的高次项。参照有功网损的分配方式,如B系数法和平均分配法等,当采用会计成本定价时,有:
(qk)为泰勒展开的高次项。参照有功网损的分配方式,如B系数法和平均分配法等,当采用会计成本定价时,有:
式中:Δ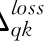 (qk)为泰勒展开的高次项。参照有功网损的分配方式,如B系数法和平均分配法等,当采用会计成本定价时,有:
(qk)为泰勒展开的高次项。参照有功网损的分配方式,如B系数法和平均分配法等,当采用会计成本定价时,有:
式中:ηqk为无功网损分配系数,当按比例进行分配时,网损系数![]() 同样道理,假设无功功率与节点电压强关联,对于节点电压上限、下限约束,当采用会计成本定价时,令:
同样道理,假设无功功率与节点电压强关联,对于节点电压上限、下限约束,当采用会计成本定价时,令:
式中:ηqk为无功网损分配系数,当按比例进行分配时,网损系数![]() 同样道理,假设无功功率与节点电压强关联,对于节点电压上限、下限约束,当采用会计成本定价时,令:
同样道理,假设无功功率与节点电压强关联,对于节点电压上限、下限约束,当采用会计成本定价时,令:
同样可以定义![]() 分别为各个节点无功注入对节点电压的影响因子。可以将V
分别为各个节点无功注入对节点电压的影响因子。可以将V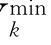 -Vk、Vk-V
-Vk、Vk-V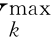 分别对qj进行泰勒展开,再求φ
分别对qj进行泰勒展开,再求φ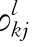 ,φ
,φ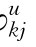 。其他的表示如第8章所示。此外,还有:
。其他的表示如第8章所示。此外,还有:
同样可以定义![]() 分别为各个节点无功注入对节点电压的影响因子。可以将V
分别为各个节点无功注入对节点电压的影响因子。可以将V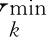 -Vk、Vk-V
-Vk、Vk-V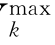 分别对qj进行泰勒展开,再求φ
分别对qj进行泰勒展开,再求φ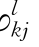 ,φ
,φ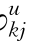 。其他的表示如第8章所示。此外,还有:
。其他的表示如第8章所示。此外,还有:
可以定义:
可以定义:
其中
其中
当采用古诺模拟时,假设有功功率与线路潮流的相关联,无功功率与节点电压相关联,令将式(9.1)~式(9.3)形成增广拉格朗日函数的形式,有:
当采用古诺模拟时,假设有功功率与线路潮流的相关联,无功功率与节点电压相关联,令将式(9.1)~式(9.3)形成增广拉格朗日函数的形式,有:(https://www.daowen.com)
分别对pk,qk求导,得到如下的最优性条件:
分别对pk,qk求导,得到如下的最优性条件:
将上式变换为:
将上式变换为:
式中:k=1,2,…,N。代入到目标函数(9.1)中,考虑到式(7.42)、式(7.44)和式(7.45),以及式(9.4)~式(9.9)得到:
式中:k=1,2,…,N。代入到目标函数(9.1)中,考虑到式(7.42)、式(7.44)和式(7.45),以及式(9.4)~式(9.9)得到:
因为:![]()
所以,式(9.2)变为:
因为:![]()
所以,式(9.2)变为:
同样道理,式(9.3)变为:
同样道理,式(9.3)变为:
令:C0M=-βp,D0M=-βq,则目标函数值变为:
令:C0M=-βp,D0M=-βq,则目标函数值变为:
则由式(9.16)~式(9.18)即构成了发电侧电力市场的一般均衡模型。
则由式(9.16)~式(9.18)即构成了发电侧电力市场的一般均衡模型。
当采用供应函数模拟时,可以定义c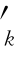 =a
=a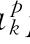 pk+b
pk+b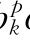 qk+c
qk+c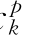 ,d
,d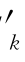 =a
=a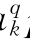 pk+b
pk+b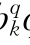 qk+c
qk+c 作为会计成本定价时的市场参与者k的有功和无功电价,代替上面的ck、dk,即可以得到与上述相同的两商品电力市场一般均衡模型。
作为会计成本定价时的市场参与者k的有功和无功电价,代替上面的ck、dk,即可以得到与上述相同的两商品电力市场一般均衡模型。
当采用供应函数模拟时,可以定义c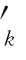 =a
=a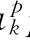 pk+b
pk+b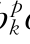 qk+c
qk+c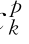 ,d
,d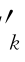 =a
=a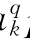 pk+b
pk+b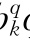 qk+c
qk+c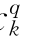 作为会计成本定价时的市场参与者k的有功和无功电价,代替上面的ck、dk,即可以得到与上述相同的两商品电力市场一般均衡模型。
作为会计成本定价时的市场参与者k的有功和无功电价,代替上面的ck、dk,即可以得到与上述相同的两商品电力市场一般均衡模型。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






