无功功率参与市场报价时,电力市场拍卖人的决策模型以式(5.13)~式(5.18)来描述,形成增广的拉格朗日函数,其形式为:
式中:Fqk(qk)表示式(5.13)所示的无功功率潮流方程;αqk为对应无功功率潮流方程的拉格朗日乘子;βq为对应无功功率平衡方程的拉格朗日乘子;k=1,2,…,NI,为起作用的节点电压下限或上限不等式约束集合;φuk、φlk分别为对应节点电压上限和下限不等式约束的拉格朗日乘子,由于节点电压的上限和下限不等式约束不能同时起作用,所以φuk和φlk有一个必然等于0。其余符号表述如上。
当采用古诺模拟时,认为市场参与者是价格的接受者,只能通过选择有功功率和无功功率的产量来最大化自己的利润。分别对pk和qk进行求导,得到如下的最优性条件:
式中:Fqk(qk)表示式(5.13)所示的无功功率潮流方程;αqk为对应无功功率潮流方程的拉格朗日乘子;βq为对应无功功率平衡方程的拉格朗日乘子;k=1,2,…,NI,为起作用的节点电压下限或上限不等式约束集合;φuk、φlk分别为对应节点电压上限和下限不等式约束的拉格朗日乘子,由于节点电压的上限和下限不等式约束不能同时起作用,所以φuk和φlk有一个必然等于0。其余符号表述如上。
当采用古诺模拟时,认为市场参与者是价格的接受者,只能通过选择有功功率和无功功率的产量来最大化自己的利润。分别对pk和qk进行求导,得到如下的最优性条件:
以及
以及
假设线路潮流只是与有功功率密切相关,节点电压只是与无功功率密切相关,则式(8.16)可以变化为:
假设线路潮流只是与有功功率密切相关,节点电压只是与无功功率密切相关,则式(8.16)可以变化为:(https://www.daowen.com)
从而得到市场上的有功和无功电价分别为:
从而得到市场上的有功和无功电价分别为:
当采用供应函数模拟时,假设供应函数如式(8.10)所示,将展开的拉格朗日函数(8.14)分别对pk和qk进行求导,得到如下的最优性条件:
当采用供应函数模拟时,假设供应函数如式(8.10)所示,将展开的拉格朗日函数(8.14)分别对pk和qk进行求导,得到如下的最优性条件:
得到市场上的有功和无功电价分别为:
得到市场上的有功和无功电价分别为:
与古诺模型相比,分别增加了(a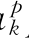 pk+a
pk+a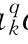 qk)和(b
qk)和(b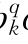 qk+b
qk+b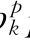 pk)两项内容。
pk)两项内容。
与古诺模型相比,分别增加了(a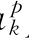 pk+a
pk+a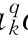 qk)和(b
qk)和(b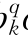 qk+b
qk+b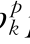 pk)两项内容。
pk)两项内容。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






