当无功商品参与市场报价时,发电商的决策模型如式(5.10)、式(5.11)所示。
8.2.1.1 古诺模拟
当电力市场采用古诺模拟时,市场参与者是价格的接受者,只能通过选择产量来最大化自己的利润。将式(5.10)、式(5.11)写成增广的拉格朗日函数的形式,有:
从而可以分别求取pk和qk为:
分别对pk和qk进行求导,得到如下的最优性条件:
以及
式中:k=1,2,…,N。如果认为发电成本只是与有功功率密切相关,即以式(5.2)来表示的话,则式(8.2)和式(8.3)变为:
从而可以分别求取pk和qk为:
在不等式约束(5.11)满足的情况下,μk=0,此时有功和无功功率是相互独立进行报价的。如上所示,此时![]() 而qk的选择在不等式约束(5.11)满足的情况下越大越好。
而qk的选择在不等式约束(5.11)满足的情况下越大越好。
当不等式约束(5.11)的等式成立时,μk不等于0,有功和无功功率的报价通过μk相互影响。当式(5.11)等号成立时,可得:
在不等式约束(5.11)满足的情况下,μk=0,此时有功和无功功率是相互独立进行报价的。如上所示,此时![]() 而qk的选择在不等式约束(5.11)满足的情况下越大越好。
而qk的选择在不等式约束(5.11)满足的情况下越大越好。
当不等式约束(5.11)的等式成立时,μk不等于0,有功和无功功率的报价通过μk相互影响。当式(5.11)等号成立时,可得:
将式(8.6)和式(8.7)代入后,得到:
将式(8.6)和式(8.7)代入后,得到:(https://www.daowen.com)
解得μk并回代到式(8.6)和式(8.7)中,即可以得到发电商的最优投标策略pk和qk,它们都同时是有功电价ck和无功电价dk的函数。在实际的竞价过程中,为了充分利用发电机组的容量,可以认为式(8.8)是必须满足的。也就是说,μk总是不等于0的。
8.2.1.2 供应函数模拟
当电力市场采用供应函数模拟时,发电商的有功和无功报价都分别是有功和无功功率的函数。如果供应函数以线性函数的形式来表示,有:
解得μk并回代到式(8.6)和式(8.7)中,即可以得到发电商的最优投标策略pk和qk,它们都同时是有功电价ck和无功电价dk的函数。在实际的竞价过程中,为了充分利用发电机组的容量,可以认为式(8.8)是必须满足的。也就是说,μk总是不等于0的。
8.2.1.2 供应函数模拟
当电力市场采用供应函数模拟时,发电商的有功和无功报价都分别是有功和无功功率的函数。如果供应函数以线性函数的形式来表示,有:
将式(8.10)联立求解,得到:
将式(8.10)联立求解,得到:
将上述公式代入到式(8.1)中,分别对线性供应函数的系数a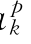 、b
、b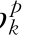 、c
、c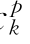 、a
、a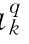 、b
、b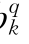 、c
、c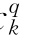 进行求导,联立方程式(8.8),并根据市场上确定的电价ck和dk,确定最佳的报价策略(确定报价系数a
进行求导,联立方程式(8.8),并根据市场上确定的电价ck和dk,确定最佳的报价策略(确定报价系数a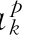 、b
、b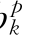 、c
、c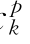 、a
、a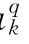 、b
、b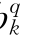 、c
、c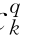 )。
)。
当不等式约束(5.11)的不等号成立时,μk等于0,求解上述问题不需要联立方程(8.8)。
将上述公式代入到式(8.1)中,分别对线性供应函数的系数a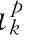 、b
、b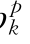 、c
、c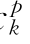 、a
、a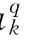 、b
、b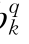 、c
、c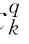 进行求导,联立方程式(8.8),并根据市场上确定的电价ck和dk,确定最佳的报价策略(确定报价系数a
进行求导,联立方程式(8.8),并根据市场上确定的电价ck和dk,确定最佳的报价策略(确定报价系数a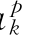 、b
、b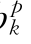 、c
、c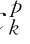 、a
、a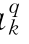 、b
、b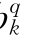 、c
、c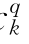 )。
)。
当不等式约束(5.11)的不等号成立时,μk等于0,求解上述问题不需要联立方程(8.8)。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。





