如上所述,无论对普通的市场参与者采取什么样的模拟方式,当电力市场拍卖人采用供应函数或需求函数模拟时,使最简单电力市场能够达到纳什均衡,而不能达到竞争性均衡。因此,供应函数或需求函数模拟很适合于不完全竞争的市场。
由第3章分析可知,电力市场的定价方式主要有会计定价和边际成本定价两种,因为电力市场还需要严格的管制,所以这两种定价方式在电力市场中都是可以应用的,选择不同的定价方式可以作为电力市场拍卖人决策的一种手段。
对于普通市场参与者k来说,其市场上的收入可以表示为:πk=ckpk。无论采用古诺模拟还是采用供应函数(需求函数)模拟,当采用边际成本定价时,电价表示单位产量的变化引起收入的变化。因此,市场参与者的电价可以表示为:
当采用古诺模拟和供应函数(需求函数)模拟时,?分别等于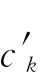 和
和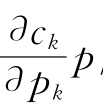 +ck,所以采取供应函数模拟时达不到竞争性均衡。
+ck,所以采取供应函数模拟时达不到竞争性均衡。
当采用会计成本定价时,关键是如何分摊市场参与者的收入。例如采取邮票法,市场参与者的电价可以表示为:
当采用古诺模拟时,c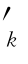 =ck;当采用供应函数模拟时,c
=ck;当采用供应函数模拟时,c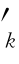 =a
=a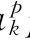 pk+c
pk+c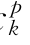 =ck。
=ck。
当采用会计成本定价方式时,无论采用古诺模拟还是供应函数(需求函数)模拟,电力市场拍卖人的决策可以变化为:
当采用古诺模拟时,c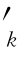 =ck;当采用供应函数模拟时,c
=ck;当采用供应函数模拟时,c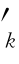 =a
=a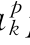 pk+c
pk+c =ck。
=ck。
当采用会计成本定价方式时,无论采用古诺模拟还是供应函数(需求函数)模拟,电力市场拍卖人的决策可以变化为:
这与式(4.5)是等价的,c′k表示按照会计成本所定的电价。因此,式(4.10)变化为:
这与式(4.5)是等价的,c′k表示按照会计成本所定的电价。因此,式(4.10)变化为:(www.daowen.com)
式(4.11)及式(4.22)变化为:
式(4.11)及式(4.22)变化为:
将式(4.29)代入到式(4.27)中,即可以得到如式(4.7)和式(4.13)所示的竞争性均衡模型
因此,可以得出结论:对于最简单的电力市场,当采用会计成本定价时,电力市场仍可以达到竞争性均衡状态。由此可见,电力市场中不同定价方式的选择,将使电力市场达到不同的均衡状态。
当采用会计成本定价时,还有:
将式(4.29)代入到式(4.27)中,即可以得到如式(4.7)和式(4.13)所示的竞争性均衡模型
因此,可以得出结论:对于最简单的电力市场,当采用会计成本定价时,电力市场仍可以达到竞争性均衡状态。由此可见,电力市场中不同定价方式的选择,将使电力市场达到不同的均衡状态。
当采用会计成本定价时,还有:
即电力市场的竞争性均衡模型是电力市场优化决策模型成立的必要条件,而不是充分条件。
即电力市场的竞争性均衡模型是电力市场优化决策模型成立的必要条件,而不是充分条件。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。







