4.2.1.1 古诺模拟

当电力市场采用古诺模拟时,市场参与者只是通过选择产量来使本身的利润或效益最大化,是价格的接受者。对于普通的市场参与者来说是这样的,对于电力市场拍卖人来说,也是一样的,同样是价格的接受者,成交价格是在市场上通过竞争确定的。

对于普通的市场参与者k,当采用古诺模拟时,将式(4.2)代入式(4.1)中,并对pk求导得:

即得到了对应价格ck的最佳产量选择为:

而对于电力市场中拍卖人的决策模型式(4.5)和式(4.7)来说,当采用古诺模拟时,将式(4.5)及式(4.7)写成增广拉格朗日函数的形式,有:

式中:βp为对应功率平衡方程的拉格朗日乘子。对pk进行求导,得到:

令-βp=C0M,代入到式(4.5)中,得到:

将式(4.7)代入,即

式(4.13)、式(4.7)与竞争性均衡模型方程式(2.15)、式(2.16)有相同的形式。如果用户不参与投标,将式(4.4)和式(4.5)写成增广的拉格朗日函数的形式有:

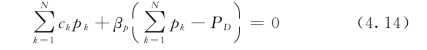
对pk进行求导,同样可以得到式(4.11)。代入目标函数式(4.5)中也同样可以得到式(4.12)。将式(4.4)代入到式(4.12)中,有:

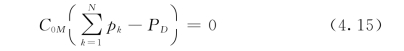
由式(4.4)与式(4.15)同样构成了发电侧电力市场的竞争性均衡模型,与式(2.15)、式(2.16)也具有相同的形式。由此可以得出结论:在古诺模拟下,由电力市场的优化决策模型可以推导出竞争性均衡模型。市场参与者的决策变为:

即

也就是说,当市场价格等于生产的边际成本时,市场参与者的效益最大化,这与完全竞争市场是相符合的。

4.2.1.2 供应函数与需求函数模拟

当电力市场采用供应函数或者需求函数模拟时,市场参与者可以同时选择产量和价格来使本身的利润或者效益最大化,也就是说,此时的电力市场参与者不只是价格的接受者,其决策将对市场价格产生影响,这不符合完全竞争市场成立的条件。采取供应函数或需求函数模拟的主要原因是很多研究者认为,电力市场不是完全竞争的市场。(www.daowen.com)

当电力市场采用供应函数或需求函数模拟时,对于市场参与者k,一般采取如下的线性供应函数或需求函数模型:

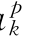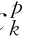式中:a、c为常系数。

将式(4.18)代入到式(4.1),并将式(4.2)代入式(4.1)中得到:

对pk求导,得:

解得:

对于电力市场拍卖人来说,式(4.10)同样成立,对pk求导,得:

将式(4.18)代入式(4.22),得到:

将式(4.18)代入到式(4.5)中,得到:

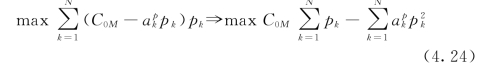
考虑到式(4.7),式(4.24)的目标函数实际上等于

由此可见,当采用供应函数或需求函数模拟时,电力市场决策的结果没有统一的边际电价,电力市场的收支也是不平衡的。

对上面的一个简单的例子,有:-6p+8=4p+4,解得p=0.4,c1=6.8,c2=4.4。如图4.4O′及O″所示,虽然供需达到了平衡,但是并没有统一的边际电价。阴影部分面积等于

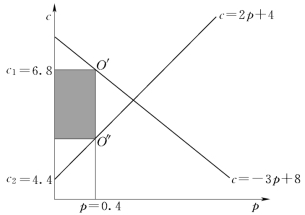
图4.4　供应函数模拟示意图

也就是说,采用供应函数或需求函数模拟时,不能由电力市场的优化决策模型得到竞争性均衡模型。

4.2.1.3 电力市场的纳什均衡

由于将电力市场拍卖人看成一个特殊的市场参与者,所有的市场参与者都是以利润最大化为目标的,那么由式(4.1)、式(4.5)及式(4.7)组成的电力市场决策模型有解时,这个解必定是纳什均衡解,无论是采用古诺模拟还是供应函数(需求函数)模拟。

但是,如式(4.1)、式(4.5)及式(4.7)组成的电力市场决策模型有解时,并不一定能达到竞争性均衡。采用古诺模拟时,竞争性均衡是可以达到的；而采用供应函数(需求函数)模拟时,则达不到竞争性均衡。