“系统”的视角一直贯穿本书的分析过程，因为“系统”是真实世界中事物存在的基本形态，是信息技术应用的本质特征之一，更是开创信息技术智能化未来的创新基点。

在第2章第2.1节中曾经指出：“从技术的角度，特别是系统学的角度来看：由于应用软件大多数情况下是在一个几乎无资源限制的虚拟空间内随意编制的，除了逻辑规则之外，没有其他客观规律的制约，从而导致大型应用软件系统的复杂度在快速增加，其复杂度远远超过了一般的物质化实体系统。因为实体系统有物理规律等方面的硬性限制，其设计构造不能随意发挥，所以其复杂度不可能随意扩张。而软件的开发则非常不同，系统的复杂性只受到设计人员思维能力甚至仅仅受他们的主观意愿的限制。”

随着信息技术产业跨过今天这个关键的转折点，使得计算机的处理能力在绝大多数形况下不再是应用的瓶颈，那些主要由软件构成的信息技术信息类应用的系统将日趋复杂。

回到现实中来，从工程实现的角度提一个现实性的问题：在没有物理限制的虚拟空间中，我们可以发挥自己的创意将系统设计得任意复杂，并让其遵循设计的原理和初衷可靠地工作吗？且不管这些原理是否正确。

人类科技发展的一个重要使命就是借助工具不断拓展人类能力的边界、体力或脑力。在前面讨论的内容也属于这个范畴。但是，这种拓展并非是可以随心所欲或漫无边界的。所以，确定各种工具与方法能力的边界极限也是科技探究的重要问题之一。而且对极限的认识可以让人类的努力减少盲目性，更加具有自觉性。比如，山农在其论文《通信的数学理论》中给出的第一个定理，就是如何确定无噪声离散信道的理论通信容量，也就是通信信道能力的上限。

我们无法预测未来会出现哪些构型各异的智能化系统，因为这些创新一如区块链及以虚拟映像为基础的融合服务系统那样，是面对真实问题而出现的超越已有模式与框架的创新。但是，对复杂人工系统的“边界”问题进行基本的一般性分析，对信息技术未来的系统级创新具有重要的现实指导意义。

随着复杂度的增加，系统的有效性与可实现性成为一个重要的问题。首先来看一下有效性的问题。

如图8-15所示，当一个系统仅仅实现了基本功能的时候，系统常常是手工实现的，它的效能是非常有限的。随着系统功能复杂度增加，信息技术常常开始支撑系统的实现。系统的效能会持续提升。但是，随着系统复杂度的增加，效能提升并不总是一个单调上升的曲线。

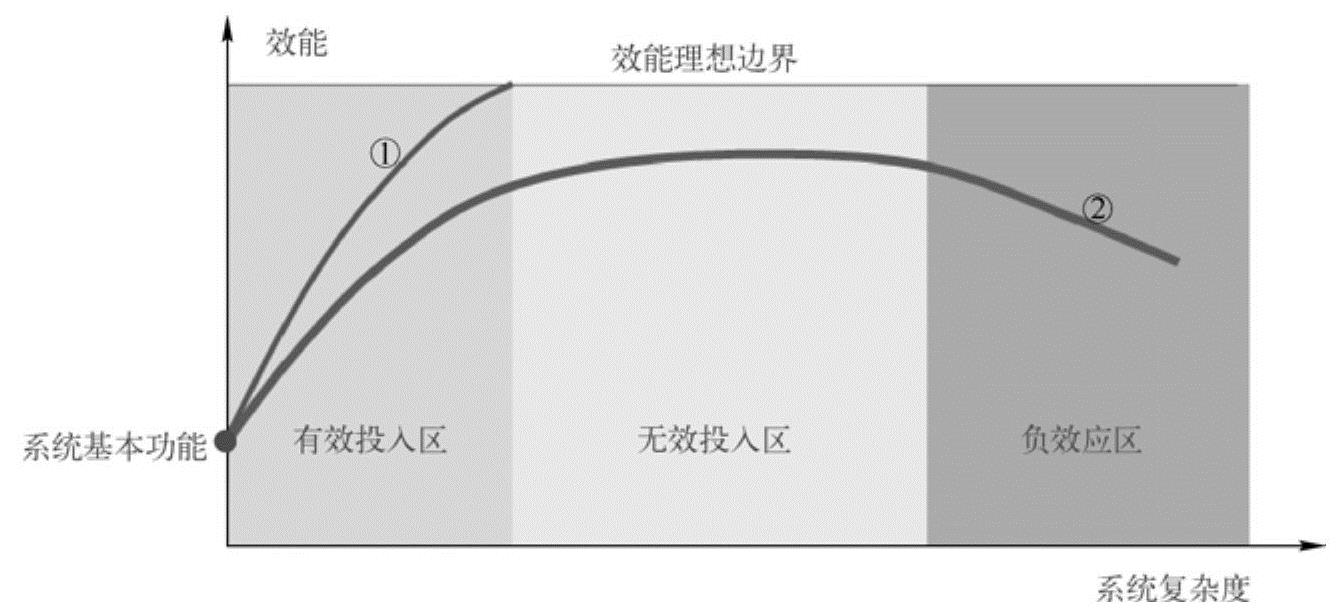
图8-15 系统的有效性

图8-15中，曲线1的情况是系统所需要实现的功能具有严格的逻辑规范。在这种情况下，随着系统复杂度增加，系统效能也持续提高，直到系统完全实现所有的逻辑规范。这时系统全面满足需求，并且效能也达到理想的边界。

但这只是一种比较特殊的情况。大多数情况下，特别是随着信息技术应用范围的不断扩展，系统需要实现的功能并不都是完全由严格逻辑来规范的。或者说，需求不能完全被逻辑化。这个时候，随着系统复杂度的增加，出现了三个不同的区域。第一个是有效投入区。在这个区域内，系统的效能与系统的复杂度及系统建设的投入是成正向关系的。但是，系统复杂度增加到一定程度后，将进入“无效投入区”。这个时候，系统复杂度的增加不再对系统的效能有贡献，所以这个时候的投入实际上是无效的。如果投入继续增加，就出现了“负效应区”。这个时候，系统复杂度/投入的增加将导致系统效能的下降。

之所以会出现这种情况，主要有以下两个原因。

（1）有些需求是不能全部用形式化的逻辑来描述的。如果超出了这个界限，新增加的形式化逻辑描述对于系统的效能并没有贡献，甚至有负面影响，因为它可能扭曲了系统整体的功能。以员工考评为例，为了更准确地评价员工，现在已经发展到对员工作所谓的360°的量化考评。这已经超出了管理规律的合理范围，带来了负面的影响。

（2）任何系统的运行都是有开销的。这其中有两个主要因素。一个是维持系统正常运营并使用系统来解决问题时所付出的劳动；另一个就是任何信息技术系统都需要人适当的行为改变，这种改变也会造成相应的付出。这种系统运营开销随着系统复杂度增加而增加。当它的增量与系统效能的增量一样时，系统复杂度的增加就不再带来效能的提升。而当系统运行的开销增量超过系统效能提高的增量的时候，便进入了“负效应区”；当然，信息技术的发展中很重要的一个方向就是不断降低信息技术系统的运行开销，但是只能减少，而不能消除。

所以，虽然软件系统可以几乎无限制地增长，但我们要小心地衡量，一个系统的复杂度到底应该做到什么程度才是一个合理的平衡点。只有对需求、系统的运营以及对应用对象的影响、信息技术发展水平等进行全面的评估，才能找到这个平衡点。这个平衡点也是随时间变化的。我们可以发展出一些更加细化的指导原则，但是并没有一个完整而严格的可操作逻辑程序能够完成这个评估。

上面谈到的是系统的有效性问题。随着系统复杂度的增加，尽管系统可能已经进入“负效能区”，但是它依然是可以正常运行的。如果系统复杂度继续增加，我们可能会遇到另一个更为严重的问题，就是系统崩溃的局面。系统的“有效性”问题转变为系统的“可实现性”问题。

当年，美国成功地发展出航天飞机这种革命性的天地运载工具，但是由此也酿成了人类航天史上的两次空前巨大的悲剧。在航天飞机投入使用后的第5年，1986年1月28日上午，美国航天飞机“挑战者”号从佛罗里达州卡纳维拉尔角肯尼迪航天中心的发射架上升空。73秒钟后突然爆炸（见图8-16），价值12亿美元的航天飞机被炸成碎片坠入大西洋，7名机组人员全部遇难。其中包括美国37岁的中学女教师麦考利夫，她是从1万多名申请者中选拔出来的美国第一位参加航天飞行的普通公民。

(www.daowen.com)

图8-16 “挑战者”号航天飞机在发射升空时爆炸

在第1章第1.3节提到过，提出量子计算的著名物理学家费曼参与了这次事故的调查，他通过实验证实是航天飞机固体火箭助推器的密封圈在低温下变脆而引发了事故。随后，美国宇航局对航天飞机的每次发射都极为小心，但是7年后还是再次出事。2003年2月1日，载有7名宇航员的美国“哥伦比亚”号航天飞机在结束了为期16天的太空任务之后返回地球。但在着陆前发生意外，航天飞机解体坠毁，7名宇航员罹难。这次的事故原因则是航天飞机的防热瓦在发射时受损。至此，5架航天飞机损失了2架。

美国宇航局于2010年初宣布全部航天飞机在年内退役，并且不再发展后续同类型航天器。2011年7月21日，美国“亚特兰蒂斯”号航天飞机于美国东部时间21日晨5时57分在佛罗里达州肯尼迪航天中心安全着陆，结束了航天飞机的“谢幕之旅”，美国30年航天飞机时代宣告终结。

航天飞机是一个极为复杂的人工系统，其工作环境也十分恶劣。两次灾难性的事故其实表明这个系统触及了复杂系统的可实现边界。所以不论如何谨慎小心，也不能保证系统安全可靠地运行，系统的漏洞变得防不胜防。

对于一个系统的复杂度，我们主要从以下几个方面来描述：构造复杂度、功能复杂度、功能精确度及可靠性等。为了表达方便，图8-16中只显示了前三个维度。一个系统在这几个维度上都只能达到一定的要求，而不可能无限制地提升，而且不同维度之间还有相互之间的制约影响。比如，功能简单，精度通常就可以做得更高。功能的复杂度与结构的复杂度也有矛盾。SOA（面向服务的架构）的方法，就是希望在增加功能复杂度的同时尽量避免系统结构复杂度的增加。所以，在由这几个维度构成的空间中存在一个曲面，稳定有效的系统只能在这个曲面之上。这个曲面就是复杂系统的可实现边界。超出这个边界的系统，或者根本不可实现，或者将会在某些需要其正常工作的条件下发生崩溃，或者其行为表现不在其设计者预期的范围之内。

图8-17只以系统构造复杂度、系统功能复杂度与系统功能精度三个维度构成一个复杂系统的存在空间，其中由三条曲线确定的曲面就是一个复杂系统的可实现边界。

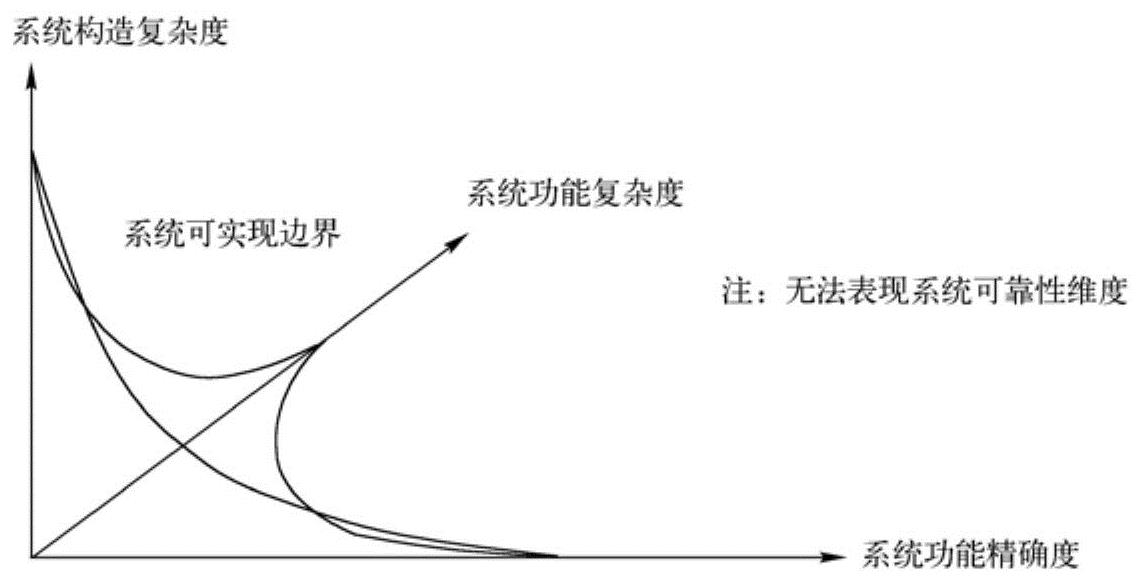
图8-17 复杂系统可实现边界的示意图

系统可实现边界显然与技术手段有直接关系。技术的发展会不断地外推这个边界。在具体的技术环境下，如何做到极致在于对技术的深刻理解与系统设计的水平。

苏联在20世纪60年代后期研制成功的米格-25飞机曾经是一个传奇，在西方造成了巨大的恐慌。甚至好莱坞在1982年拍摄了影片《火狐》（基于1977年出版的同名小说），想象苏联后续的米格-31可以用人脑思维直接操纵，实现雷达隐身并且超过音速6倍。米格-25是世界上第一种“双三”战斗机（截击机），即可以在接近3万米的高空飞行，最高飞行速度可达三倍音速。西方得知其存在及基本的性能后，判断苏联在技术上有了巨大的进步。因为当时西方难以造出具有同样性能的战斗机，美国只有一种战略侦察机SR-71可以实现“双三”指标。

后来在1976年9月6日，苏联空军上尉维·依·别连科驾机叛逃至日本，西方如获至宝（见图8-18）。但他们惊讶地发现，在这架飞机上并没有他们掌握不了的具体技术：为了应对高速飞行产生的高温，它大量使用了传统的不锈钢而不是先进的钛合金；它功能强大的雷达系统甚至还在使用旧式的真空电子管。苏联工程师通过杰出的系统设计把他们掌握的技术发挥到极致，构造出一个可以可靠完成任务的复杂系统，超出了西方同行有能力实现的系统边界。这是在本章第8.4节中讨论过的在实际应用中通过系统设计超越具体技术局限的一个经典案例。

而航天飞机则是一个相反的例子，它达到或超出了系统可实现边界，在正常使用的情况下发生了系统崩溃的惨剧。

图8-18 别连科驾驶米格-25冲出了日本函馆民用机场跑道

抛开主观愿望与意识形态等因素，全计划经济体制的本质问题也在于系统的可实现边界。在一般规模的企业里，实行的都是计划体制。在系统可实现边界之内，计划体制显然是最有效的。但是当把它推广到全社会之后，系统规模的扩大使得系统超出了可实现边界。这个时候全计划体制就没有办法持续稳定地正常发挥作用了，需要引入自发的市场机制来降低系统的复杂度。

随着信息技术跨过关键的门槛而能够提供充裕的基础技术能力，特别是处理能，我们设计的系统正在快速变得越来越复杂。在这个过程中，系统分析设计能力将变得日益不可缺少，否则我们设计的系统的效能与效果都将无法保证。而系统分析设计的方法在计算机科学的理论体系（见图2-1）中一直没有受到足够的重视。这就是本节讨论的话题的初衷。

技术的发展是否可以无限制地外推人工系统的可实现边界？这是见仁见智的问题。西方的观点倾向于随着技术的进步，这个边界可以无限外推；而东方则有不同的看法，它倾向认为人的能力是有局限的，所以不论技术如何发展，人造出的系统的复杂程度都有一个不可超越的边界。这种限制体现了自然法则，非人力可改变。在步入信息技术产业更加辉煌的时代时，我们需要在这两者之间保持一个合理的平衡。