1.基准模型的构建

基准模型的构建是空间面板分析的基础。依据城镇建设用地驱动的经济学原理与现状，参考现有文献，本章选取第二产业产值、第三产业产值、固定资产投资、地方财政支出、城镇化人口、路网密度作为解释变量，但是对这些变量选取的是其绝对值，而不是其所占比例。原因如下：首先，本章研究的是城镇建设用地面积，而不是建成区面积的年度增长率，因此是一个绝对的数值；其次，需要说明的是，现有文献大多采取第二产业或者第三产业产值比重、或者城镇化人口的比例来作为解释变量。但仔细分析可以发现，如果非农产值或者城镇人口确实对城镇建设用地具有正向推动作用，那么是那些实实在在的非农产值或者城镇人口对城镇建设用地产生了影响而不是它们的比例。举一个绝对的例子来说，一个具有100万人口的省区市，即使其城镇化了为100%，其城镇人口也是100万；一个具有1000万人口的城市，即使城镇化率为50%，其城镇人口也为500万。对于二产或者三产的比值或者其绝对值，也可以做同样的理解。部分文献认为，城镇建设用地的扩展与土地财政有关，而政府的财政收入又用于下一步的圈地造城。因而通过将地方财政支出作为解释变量可以部分检验是否存在土地财政的倒逼机制。路网密度的加快，促进了区域间、城乡间的通达性，因而其对城镇建设用地的影响也不言而喻。综上所述，考虑到中国产业集群与城市群的互相集聚，再加上交通、通讯的发展，中国建成区面积的扩展也无法摆脱客观存在的地域联系。

（1）基准模型。

式中：i表示截面维，i＝1，2，3，…，N；t表示时间维，t＝1，2，3，…，T；yit（km2）表示被解释变量在第i个截面单元第t时期的城镇建设用地观测值；xit是k维行向量，表示k个解释变量在第i个截面单元第t时期的观测值，β是k维列向量，表示相应解释变量的系数。其中，x1（万元）、x2（万元）、x3（万元）、x4（万元）、x5（万人）、x6（km／km2）分别表示第二产业产值、第三产业产值、固定资产投资、地方财政支出、城镇化人口、路网密度，βi为待估的相应系数列向量。εit是标准误差项，表示未观测到的影响因变量的其他因素。ui为反映个体差异的变量，表示省（区、市）的固定效应，θt表示时间效应。

上述若Moran I指数的检验确定了中国建成区面积的空间相关性，所以应该建立空间因素建立空间计量模型。Anselin将空间因素引入经典计量经济学模型，建立了空间滞后模型（Spatial Lag Model，SLM）和空间误差模型（Spatial Error Model，SEM）。SLM主要考察变量在各个地区的空间相关性，讨论的是变量在相邻地区是否存在溢出效应；SEM主要考察存在于误差扰动项中的空间依赖性，讨论的是相邻地区对变量的误差的影响在多大程度上影响了本地区的观察值。（2）空间滞后模型（SLM）。由于区域经济一体化的推进和城乡统筹发展，城镇建设用地存在一定的相关性，可以通过加入因变量的空间滞后因子进行分析。空间滞后模型的基本结构如下：

式中：μi表示空间固定效应，其控制了所有空间固定且不随时间变化的变量；θt则表示时间固定效应，其控制了所有时间固定且不随空间变化的变量；wij是空间权重矩阵w中的一个元素。(www.daowen.com)

（3）空间误差模型（SEM）。在模型设定过程中，很可能会遗漏一些与被解释变量有关的变量，而这些变量存在空间自相关性，同时区域间可能存在随机误差冲击空间溢出效应。因此，在某些情况下忽略误差的空间自相关性也会造成模型设定的偏误。

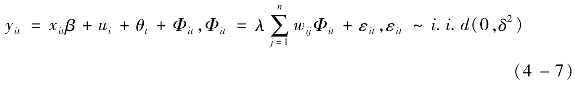
式中：Φit表示空间自相关误差项；λ表示误差项的空间自相关系数。

2.模型估计与检验

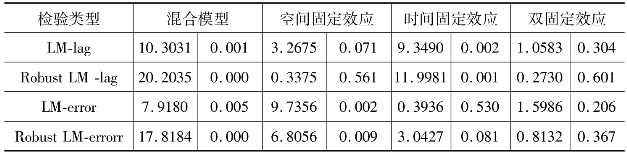
通过前述全域与局域Moran's I的计算结果，表明了纳入空间要素分析的必要性。另外，基于样本独立假设的最小二乘法对于空间依赖样本的估计是有偏差的。LucAnselin建议采取极大似然估计，并提出了如下判别准则：首先决定是否可以否定OLS估计结果，其依据是LM（lag）和LM（error）是否可以拒绝零假设。如果有一个LM检验统计量拒绝了零假设，另一个没有拒绝，则坚持没有被拒绝零假设的模型。如果两个都拒绝了零假设，则通过比较LM和Robust LM（lag）检验的显著性，采取显著性强的那个模型来构建空间回归模型。

根据上述的检验规则，检验结果见表4－5。在检验无论是LM（lag）和LM（error）都拒绝零假设，进一步比较发现LM（lag）较LM（error）更为显著，Robust-LM-lag也比Robust-LM errorr显著，因此绝对采用空间滞后模型。在滞后模型的空间效应、时间固定效应和双固定效应的估计结果中，绝大多数系数符号一致。但第三产业产值与滞后项系数略有不同。根据前述中国全域及局域空间摩尔指数的计算可见，中国省域城镇建设用地存在正的溢出效应。结合经济学基本理论及中国城镇建设用地扩展的基本现实，本章决定采取空间滞后的空间固定模型予以解释。

表4－5　空间计量模型选择比较表