国外研究中，先利用DEA模型测度出效率值，然后利用回归模型来分析出主要影响因素，是较为成熟的一种实证分析方法，即两阶段方法。对连续无界数据自变量和因变量进行回归时，一般都采用最小二乘法（OLS），但是，第一个阶段求解出的效率值是一种相对效率，效率值都处在0与1之间，如果利用普通最小二乘法（OLS）就会导致估计值有偏且不一致，为了解决这个问题，Tobin（1958）结合Probit和多次回归法提出了Tobit回归模型，该模型解决了因变量受限制的问题，采用极大似然估计法（Maximum Likelihood Estimator，MLE）对变量参数进行估计。前文运用了DEA模型选用的投入和产出指标对上市公司的货币资金使用水平进行了测度，考虑到被解释变量取值的特殊性，本节使用DEA-Tobit面板数据模型两阶段方法分析除投入和产出指标之外的对企业货币资金使用效率可能产生影响的因素。

（一）Tobit模型定义

Tobit模型也称为样本选择模型、受限因变量模型，是因变量满足某种约束条件下取值的模型。这种模型的特点在于模型包括两个部分：一是表示约束条件的选择方程模型；一种是满足约束条件下的某连续变量方程模型，但是由于因变量受到某种约束条件的制约，忽略某些不可度量（即：不是观测值，而是通过模型计算得到的变量）的因素将导致受限因变量模型产生样本选择性偏差。

（二）Tobit模型原理

Tobit模型是Tobin（1958）在研究耐用消费品需求时首先提出来的一个计量经济学模型。Tobit模型的一个主要特征是被解释变量只能以受限的方式被观测到，其值为切割值或片断值，是因变量满足某种约束条件下取值的模型。在实际研究中，样本数据为截断数据或审查数据（Truncated or Censored Data）的因变量都是受限因变量。截断数据是指观测变量在一固定的区间以外不存在观测值的数据样本，审查数据是指观测变量在一定区间外至少存在一些解释性变量的数据样本，这两个数据集都是不完整的，但是审查数据不影响样本的规模，而截断数据会减少样本的规模。Tobin（1958）提出的标准模型（第一类Tobit模型）为：

其中，i代表第i个决策单元，y'表示样本值，Xi表示响应变量，样本值yi服从以下限制：

那么样本集转化为

在由式（6-1）和式（6-2）组成的审查模型下，仅取y'＞0，样本集为（y'，Xi），此时表现为截断数据。其条件期望为：

那么，审查数据的条件期望为：

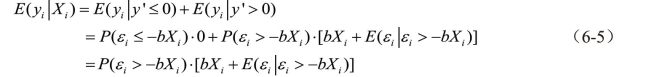
而，则：

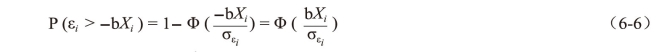
式（6-6）和（6-7）中所示Φ（.），Φ（.）分别表示累计正态分布函数和标准正态密度函数，那么截断数据和审查数据的似然函数可分别表示为：

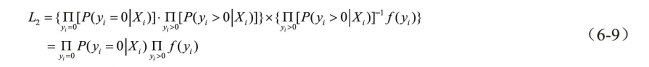
而，则：

通过式（6-8）和（6-9）可得b，σzi的极大似然值，如此可确定各响应变量的权重系数b。

由于Tobin标准模型存在非直线性，Heckman^[3]（1976）提出两步估算法：

第一步：设，基于式（6-9）和Probit函数求得δ的极大似然估计δ'；

第二步：用δ'代替δ，则截断模型表示为：

其中

不管是Tobin标准模型还是Heckman两步法，都要求ε独立同分布。事实上，ε往往是未知的，很难达到独立同分布。通过选择等式，Heckman（1979）对截断数据、审查数据的值做了外向随机计算，如式（6-16）和（6-17）所示。

其中表示外生变量，a表示参数，ui为服从均值为0、方差为1的独立正态分布。对于选择等式（6-16），有：

此外，Heckman模型中也存在连续性等式，即Tobin标准模型的形式：

那么仅有＞0的条件下，有观测值，即：

而式（6-16）—（6-19）被Amemiya（1985）命名为第二类Tobit模型。那么：

且yi，di的极大似然函数可表示为：

其中C表示集合｛i|di=0｝，在给定联合分布（ε，u）的情况下，通过式（6-21）可求得极大似然估计值。

（三）Tobit模型的分类与结构

Lee（1976）^[4]与Amemiya（1984）^[5]按照似然函数的特点，对Tobit模型进行了分类。Lee（1976）将受限因变量模型分为五类：简单的受限因变量模型、审查因变量模型、样本可分割的转换回归模型、包含指标内生变量的迭代模型、非市场均衡模型。应用中一般按照Amemiya的分类法将模型分成五类第一类模型是标准的Tobit模型，根据数据模型的不同，可建立审查数据模型或者截断数据模型，其余四类模型被称为广义Tobit模型，适用于样本选择模型。各类模型的具体结构形式如下所示：

1.第一类Tobit模型

（1）审查数据模型。当因变量被审查时，某一特定范围内的值全部变成一个单一值，下审查（或左审查）数据的一般结构为：

被审查数据回归模型的常用结构为：

根据误差项的分布特征构造似然函数：

上审查（或右审查）模型与此相反。

（2）截断数据模型。左截断数据的一般结构为：

左截断随机变量的密度分布为

被截断数据回归模型的常用形式为：，ε服从某种分布。

根据误差项的分布特征构造似然函数：

2.第二类Tobit模型

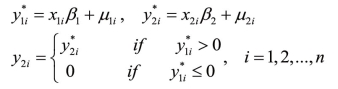
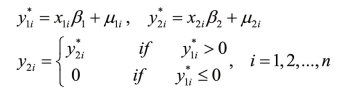(www.daowen.com)

例如：Gronau（1974）研究了家庭主妇的工资的问题，当她去工作时，才能观测到工资收入，当她不工作时，就没有工资收入的信息。

3.第三类Tobit模型

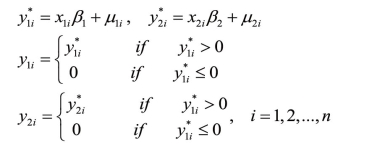
例如：Roberts和Maddala（1978）研究了企业是否决定申报提高收益率的指数。

4.第四类Tobit模型

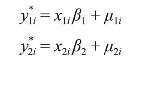
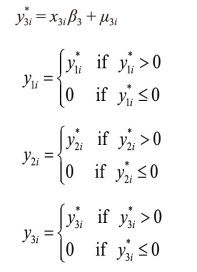
例如：Kenny（1979）利用此模型考察了上过大学与为上大学的劳动者之间的收入差异问题。

5.第五类Tobit模型

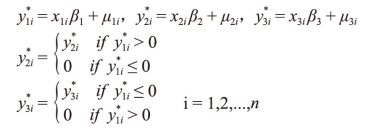
例如，Lee（1978）研究工人是否决定参加工会的问题。而此外，根据解释变量中是否包含内生变量，可以将Tobit模型分为非联立方程模型、联立方程模型。也可由实证分析所用数据的特征，可以将Tobit模型分为截面Tobit模型、时间序列Tobit模型、面板Tobit模型。

（四）Tobit面板数据模型原理

样本数据一般分为截面数据、时间序列数据和面板数据。随着面板数据的流行，各种与面板数据相关的模型和方法也成为研究热点。Tobit面板数据模型为面板数据的一种处理模型，它是建立在面板数据上的因素分析法。Tobit面板数据模型的分析过程包括固定效应Tobit模型（Fixed Effect Tobit Panel Data Model）和随机效应Tobit模型（Fixed Effect Tobit Panel Data Model）。固定效应Tobit模型是以个体特异性变量（Individual Specific Variables）为固定变量为前提的，而随机效应则是以个体特异性影响（Individual Specific Effects）为随机变量为前提的，如式（6-22）。

其中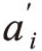为常数，b'为常数向量，εit为随机误差项，服从均值为0、方差为独立正态分布。式中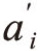则为固定变量，因此式（6-22）为固定效应模型。它能在弱假设下使用面板数据建立因果关系，但其缺点也较为明显：

（1）无法估计不随时间变化的个体特殊效应。

（2）可以估计随时间变化的解释变量的系数。但如果对解释变量的变化主要是由于截面变化引起而不是时间变化引起的，则估计值非常不精确。

（3）条件均值无法预测。线性情形下可以估计边际效应，非线性情形下甚至连系数都难以估计。

对比随机效应模型和固定效应模型，随机效应模型相当于把固定效应模型中的截距项看成两个随机变量，一个是截面随机误差项εit，另一个是时间随机误差项uit。当两个误差项服从正态分布时，模型估计可减少自由度，此时只需估计两个误差项的均值、方差；当各单元个体特异性的影响uit为随机项时，式（6-22）中εit可表示为：

所以，随机效应模型可表示为：

当固定效应模型得不到一致性的估值时，可采用随机效应Tobit模型进行分析：

其中，随机误差项uit与xit独立，并服从独立正态分布。若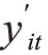＞0，观测值yit=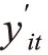；若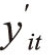≤0，当数据为截断数据时，yit不可观测，当数据为审查数据时，yit=0。设ai服从随机分布，密度函数为g（a），则关于截断数据、审查数据的似然函数分别为：

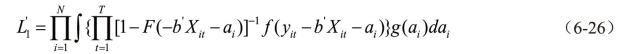
其中∫（·）是uit的密度函数，且；

其中Ci表示集合｛t|yit=0｝，为补集。

关于第二类随机效应Tobit模型则需要一个选择函数：

若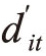＞0，dit=1，此时yit等于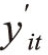；若d'it≤0，dit=0，此时yit不可观测，产生观测集（yit，dit）。设（ai，ηi）的联合密度函数为g（a，η），那么第二类随机效应Tobit模型的似然函数为：

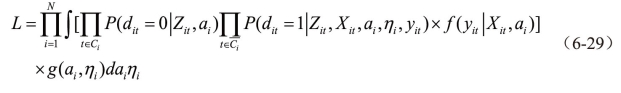
当N，T趋于无穷大，基于似然函数式（6-26）、（6-27）和（6-29）可解得未知参数b。

目前，DEA-Tobit两阶段分析方法被运用于不同机构的经济效率评价上，如Grabowski、Rangan和Rezvanian（1994）运用两阶段方法分析了美国215家银行的效率和影响因素，Sathye（2003）运用两阶段方法测度了作为发展中国家印度的银行产出效率。国内学者运用该方法测算中国商业银行效率（吴献金和罗四维，2003；朱南等，2004；陈敬学等，2004）、铁路系统效率研究（李兰冰，2008）、政府绩效研究（马雁军，2008）、医院等卫生系统效率研究（庞瑞芝，2006）、农业系统效率研究等（涂俊和吴贵生，2006）、高新区技术效率（王艺明，2003）等，这些研究成果为本章提供了研究基础和研究方法的保证。目前，运用两阶段法对企业货币资金使用效率进行实证分析的研究成果极少，为了更好地分析研究企业货币资金使用效率在时间维度和截面维度的变化情况，本章在DEA模型测度货币资金使用效率的基础上，采用面板数据，运用Tobit回归模型分析效率的影响因素。在实际应用中，可以通过检验误差项与解释变量之间的相关性来区分应该采用固定效应Tobit模型还是随机效应Tobit模型。Hausman（1978），Hausman和Taylor（1981）提出的Hausman检验是对残差与自变量之间是否存在相关关系的检验。如果模型中残差是随机变化的，与自变量没有关系，模型可以确定为随机效应模型；如果模型中残差与自变量具有相关性，对模型的影响具有可测性，可考虑为固定效应模型。本章应用Hausman检验上市公司货币资金使用效率面板数据进行检验时，不拒绝残差与自变量不相关的原假设，所以Hausman检验建议选取随机效应Tobit模型。从模型假设来看，随机效应模型既使用了个体内信息，又使用了个体间信息，而固定效应模型只使用了个体内信息，在根本上忽略了个体间差异的信息。如果自变量取值在个体间存在很大差异，而在同一个体不同时点上的变化不大，那么固定效应估计将很不准确，即固定效应模型无法控制随时间而发生变化的未观测的变量（Allison，2012）。从研究目的和样本选择来看，固定效应模型试用于考察“固定”样本内的样本间的个体差异，而随机效应模型试用于在总样本区间内，“随机”抽取样本，通过考察样本的特征推算总样本特征。本书选取861家上市公司作为样本企业，分析影响上市公司货币资金使用效率的因素，目的不仅限于考察这861家上市公司个体间的影响因素差异，而是为了分析这861家上市公司所代表的中国沪深A股市场上市公司货币资金使用效率的影响因素。因此，从模型检验、模型原理和研究目的看来，本章使用的实证分析模型应该选用随机效应Tobit模型。

（五）模型构造

在计量模型的构造中，将所有因素详细描述并且纳入计量模型中是不现实的，基于上述研究假设和模型选择，本章在国内外对企业资金效率影响因素相关研究的基础上，考察经济环境、政策法规、区域因素、市场发展、公司治理和公司经营状况是否影响中国上市公司的货币资金使用效率，以及这些因素对货币资金使用效率存在的效应。因此，被解释变量是上市公司货币资金使用效率值，解释变量是经济环境、政策法规、区域因素、市场发展、公司治理和公司经营状况。

1.模型一

依据研究假设和已有的经验性研究，式（6-30）是本章检验企业内部因素和外部因素对其货币资金使用效率影响的基本回归方程，具体如下：

其中，

ωit为合成误差项，ξi为个体误差项，μit为时间序列和横截面混合的误差项。

式（6-30）中，EFFit将分别代表第i个样本上市公司第t年应用DEA模型测算出来的技术效率（TE）、纯技术效率（PTE）和规模效率（SE），α代表回归式的常数项，Macit指影响企业货币资金使用效率的外部因素，包括经济环境（lnGDP）、政策法规（fdeep）、区域因素（lnpr_fdi）、市场发展程度（fd和in_fdi）；Firmit指影响企业货币资金使用效率的内部因素，包含公司治理水平和公司经营状况，其中公司治理选取了产权性质（firmc）、分红（divi）、高管薪酬（lnpay）、高管人数（lnch_n）等4个指标，公司经营状况选取了公司规模（lnsize）、上市年龄（age）、员工人数（lnem_n）等3个指标，各变量详细的计算见表4-2所示。

2.模型二

式（6-30）中的解释变量都为当期（即t期）时期指标，然而，在公司的实际运营中，上一年度（t-1期）的经济状况和公司运营状态会对下一年度（t期）企业的货币资金使用效率产生影响，例如企业的货币资金持有量的多少在一定程度上受到上一期宏观经济形势的影响，2008年国际金融危机爆发以后，企业界都秉持着“现金为王” 的理念，大幅度地提高企业货币资金的持有比率，这种高额持有的现象一直持续到2010年，在一定程度上也影响了企业货币资金使用效率，但是相对于企业因资金持有不足，而引发的破产危害，出于预防动机的高额持有更可取。此外，企业上一期（t-1期）的公司规模也将影响企业当期的货币资金使用效率，例如企业因上一期（t-1期）的公司规模存在冗余，而导致企业运营效率偏低的时候，公司的决策层将会在来年（t期）对公司规模做出相应的调整，以提高企业的运营效率。因此，本章将引入滞后变量，进一步分析可能对当期企业货币资金使用效率产生影响的滞后变量。具体如式（6-31）所示：

其中，Lagit-1指影响企业货币资金使用效率的滞后一期的变量，包含上一期的国内生产总值（lnGDPt-1），上一期省域FDI（lnpr_fdit-1），上一期行业FDI（in_fdit-1）和上一期公司规模（sizet-1）。由前文可知，不同的省域上市公司的数量、财政扶持力度、资源配置状况、外商直接投资额等都具有一定差异，上一期的外商直接投资对该省域资本市场当期的资本存量和企业间竞争程度都具有引导作用，故而会影响企业当期的货币资金使用效率。不同行业的外商直接投资资金分配状况不同，外商直接投资较多的行业，企业间的竞争更为激烈，该行业内的企业的货币资金使用效率可能更高，上一期的行业FDI对当期企业的货币资金使用效率具有一定引导作用和影响。

3.模型三

由随机效应模型可知，式（6-30）和式（6-31）对样本企业的个体差异和时间差异进行了控制，但是不同行业的上市公司经营特征不同，行业内企业的竞争程度不一样，因此，式（6-32）中，将加入行业虚拟变量，考察企业由于所处的行业门类是否对其货币资金使用效率值有影响。

其中，指依照中国证监会于2001年4月4日发布的《上司公司行业分类指引》，选择了除金融、保险类上市公司的12个门类的中国上市公司虚拟变量，其中综合类为基准组，共计11个行业虚拟变量，以综合类为基准组^[6]，分析不同行业上市公司间的货币资金使用效率差异。

4.模型四

式（6-30）和式（6-31）对样本企业的个体差异和时间差异进行了控制，但是不同区域内的上市公司数量不同，国家对各区域的发展规划、财政扶持力度和省域间的资源禀赋都具有一定区别，式（6-33）加入了省域虚拟变量，考察不同省域的企业的货币资金使用效率是否具有差别，即地域因素对企业资金使用效率的影响。

其中，Proit是中国31个省域的虚拟变量，以重庆为基准组^[7]。

5.模型五

式（6-32）和式（6-33）分别加入了行业虚拟变量和省域虚拟变量；式（6-34）加入了行业虚拟变量和省域虚拟变量，同时控制了行业及省域对上市公司货币资金使用效率的影响，考查主要变量对企业货币资金使用效率的影响，并对不同的省域及行业对上市公司货币资金使用效率的影响进行分析。

模型中的变量定义及计算方法详见表6-1所示。

表6-1　变量定义

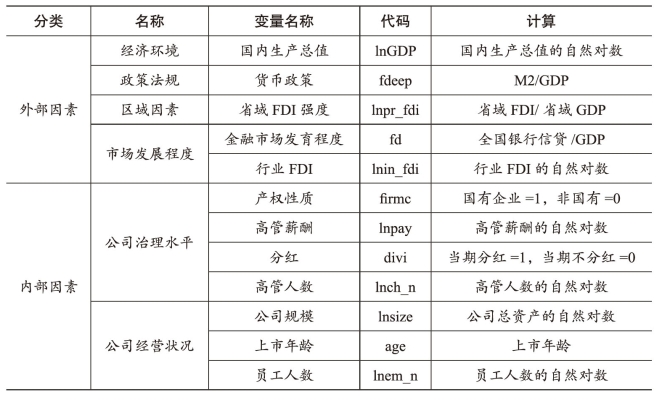
在回归分析时，国内生产总值（lnGDP）取历年国内生产总值的自然对数。选择金融深化（fdeep）即当年广义货币供应量与当年GDP的比值来反映货币政策。国外学者通常使用利率来反映货币政策的松紧与变化，由于发达国家市场化程度较高，利率是主要的货币政策工具，利率的变化能够很好地反映出货币政策的立场，但中国利率市场化程度不高，国家对银行存贷款利率存在一定的限制，因此，利率不适合作为衡量中国货币政策立场的指标。在中国货币政策调整中，央行主要使用的是数量型工具，即广义货币供应量（M2），通过对货币供应量的调整，来调整市场的总需求，因此，M2/GDP实际衡量的是在全部经济交易中，以货币为媒介进行交易所占的比重，该比率反映了一个经济体的金融深度，是衡量一国经济金融化的初级指标。通常来说，该比值越大，说明经济货币化的程度越高，宽松的货币政策有效降低了上市公司的融资约束，当公司面临较好投资机会时，宽松的货币政策使得投资机会能够更好地引导公司的投资决策，从而提高了公司的资本配置效率。外商直接投资将从外源融资和行业内竞争两个方面影响本土企业的资金使用效率，因此，省域FDI强度（lnpr_fdi）即当年省域FDI总额与当期省域GDP总量之比反映该区域境外投资对企业融资量的影响程度；行业FDI（lnin_fdi），即行业FDI总额的自然对数，反映不同行业外商直接投资对该行业市场发展程度的影响。选择银行信贷总额与GDP的比值反映金融市场发育程度（fd），与大多数发展中国家类似，银行系统在中国金融体系中占据着主导作用，扮演着关键的角色（Allen等，2005；Allen和Carletti，2008），同时，由于中国股票和债券市场发展时间太短，又受到了国家政策的严格管制，故度量金融发展的指标时舍弃了股票和债券市场发展指标，主要以银行信贷作为衡量金融发展水平的指标。

企业的产权性质是影响企业运行的重要因素之一，新制度经济学尤其强调产权归属对企业产生的影响。产权安排不仅会影响企业股东构成情况，而且会影响企业管理层的稳定，以及企业行为方式。当企业产权确定时，可以有效避免搭便车行为，理顺股东和管理层的激励约束机制，减少企业运行中的摩擦成本，降低不确定性，调动行为主体的积极性，提高企业运行效率，这一点在中国尤为明显。设定产权性质为虚拟变量，国有控股公司用1表示，非国有股份制用0表示。lnpay表示管理层的薪酬，以公司所有高管人员的薪酬总额的自然对数表示。Inch_n表示高管人数以高管人数的自然对数表示。设定企业的现金分红为虚拟变量，当期实施现金分红政策的企业为1，否则为0。中国处于市场经济快速发展的阶段，一方面公司规模越大，越有利于利用现有资源获得有潜力的项目；另一方面规模的扩大，可以产生规模效应。选择上市公司资产总额作为衡量公司规模大小的代理变量，尽管衡量公司规模有时还会涉及公司的营业收入、利润和净资产，但企业的资产总额更能全面地反映企业规模状况，例如高新技术开发企业若处于研发期，此时的企业营业收入、利润可能很低，但是该企业的总资产有可能非常庞大，尤其是研发资本雄厚企业，这种情况用公司的营业收入、利润和净资产代替企业的规模就会出现偏颇。因此，公司规模（lnsize）变量，用公司总资产的自然对数表示。