Malmquist指数法可以用来测量一个特定的公司，从时期t到时期t+1^[2]的全要素生产率的变化。Nishimizu和Page（1982）使用了Aigner和Chu（1968）的线性规划的方法估计超对数生产前沿面，并且提出全要素生产率增长的测度是效率变化和技术进步之和。其中，最有影响的是Färe等（1994）采用Caves，Christensen和Diewert（1982）定义的全要素生产率增长的Malmquist指数，他们把Malmquist指数的变化和测度分解为不同的部分，包括技术进步和技术效率变化，并说明了如何采用相对于DEA前沿面的距离来测度这些效率值。下面描述的内容主要是取自Färe等（1994）的研究论文。

（一）Malmquist指数法

Malmquist指数方法是采用面板数据，在距离函数的基础上，求出可以做垂直比较分析的效率指数，即通过计算每一个数据点相对于一个普通技术的距离比率，来测量两个数据点之间的全要素生产率的变化。假设时期t的技术被用来当作参考技术，（qt，xt）为时期t的投入和产出向量，（qt+1，xt+1）为时期t+1的投入和产出向量，用表示以t时期技术为参照的时期t的投入产出向量的产出距离函数，用表示以时期t技术为参照的时期t+1的投入产出向量的产出距离函数，那么从时期t（基期）和时期t+1之间的Malmquist（面向产出）的指数，可以写成

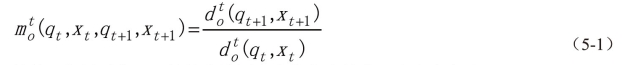
另外，如果时期t+1的技术被用来当作参考技术，那么定义为

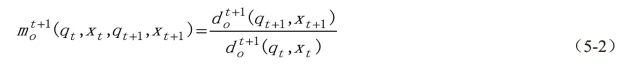
上面的等式中，符号代表从时期t的观测到时期t+1的技术的距离。其中，以时期t技术为参照，上式（5-1）表示由投入产出向量（qt+1，xt+1）所在生产前沿面向可变投入产出向量（qt，xt）所在生产前沿面调整的比率，以时期t+1的技术为参考面。同理，当mo＞1时，意味着从时期t到时期t+1全要素生产效率呈正增长，说明决策单元资源配置效率提高；当mo＜1则意味着全要素生产效率的降低，说明决策单元资源配置处于一种冗余状态，是非有效的，仍然有一部分资源尚未充分利用；当mo=1时说明决策单元资源配置是有效的，所有投入要素都发挥了最大的作用。

（二）Malmquist指数的分解

Malmquist指数法不仅可以对不同时期决策单元进行效率变化的测度，还可以通过其分解指数详细了解综合效率变化的根源。Färe等（1994）运用两个Malmquist指数的几何平均值来计算定向产出的Malmquist指数，即：

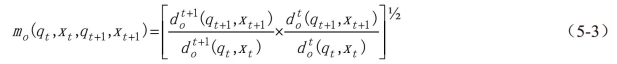
将这个生产率指数里的距离函数重新整理，得出如下形式：

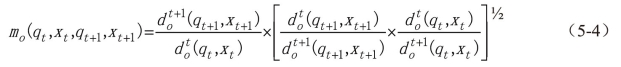
可以观测到，上面方程括号外平方的比率是测量在时期t和时期t+1之间Färe技术效率在产出方向上的测度变化。也就是说，效率变化指数与时期t的Färe技术效率到时期t+1的Färe技术效率的变化比率是相等的。因此，Färe等（1994）将Malmquist指数分解为规模报酬不变假定下的技术进步（TC）和效率变化^[3]（EC），即：

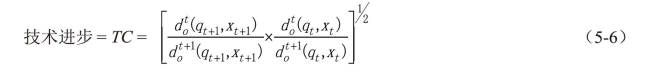
对于效率变化和技术进步有许多可能的分解，很多学者都提出了相关的建议，例如Färe等（1994）认为效率变化可以分解为规模效率和纯技术效率两部分^[4]（仅当采用相对于CRS技术估计上面方程中的距离函数时，才能进行这种分解）；Färe和Grosskopf（1996）把技术进步分解为若干的投入偏差、产出偏差和“量级”三部分。其中Färe等（1994）涉及规模效率的分解方法被广泛采用，并且（近些年来）也受到了广泛的评论。这个分解方法首先采用式（5-5）中的模型计算效率变化^[5]（现在需要假设：该比率为两个CRS距离函数的比率），然后将其分解为纯效率变化（采用相对于有争议的真实VRS前面的测度）^[6]和规模效率变化（SE），即：

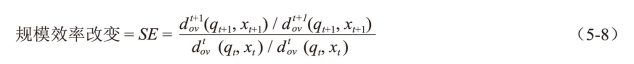
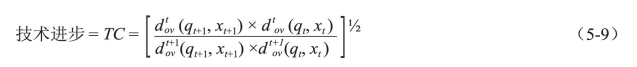
上式中，规模效率变化的部分实际上是两个规模效率变化测度的几何均值。第一个是相对于时期t的技术，第二个是相对于时期t+1的技术。下标v和c分别对应于DEA-VRS模型和DEA-CRS模型。因此，Malmquist指数可以表达为：

(www.daowen.com)

如果M＞1，代表企业从时期t到t+1，全要素生产效率增加；M=1，说明企业从时期t到t+1的全要素生产效率停滞，没有增加也没有下降；M＜1，说明企业从时期t到t+1的全要素生产效率呈下降状态。其中，效率变化（MEC）代表前沿面的追赶效应，MEC＞1，表明企业在t+1时期比t时期更接近生产前沿面，技术效率得到了有效改善；MEC=1，表明企业在t+1时期和t时期与生产前沿面的距离相等，技术效率停滞；MEC＜1，表明企业在t+1时期比t时期远离生产前沿面，技术效率下降。而技术进步（MTC）指数衡量生产前沿面的变化，它用于评价该决策单元位于生产前沿面的其他评判单元的改善或退化情况。MTC＞1，意味着技术进步；技术无变化时，MTC=1；技术出现倒退时，MTC＜1。

（三）Malmquist指数求解

很多不同的方法可以用来估计生产技术，因此用于计算Malmquist指数的距离函数的方法同样也有很多。目前，最流行的方法是Färe等（1994）提出的与DEA相似的线性规划方法。对于第i个企业，需要计算4个距离函数来测量时期t和时期t+1的全要素生产率的变化。采用DEA-CRS模型，假设所有投入都与（正的）标量δ相乘，则所有产出都为原来的（非负的）α倍，即TEP=α/δ，求解下面4个线性规划问题：

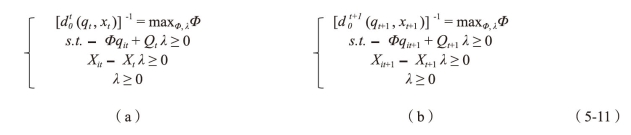
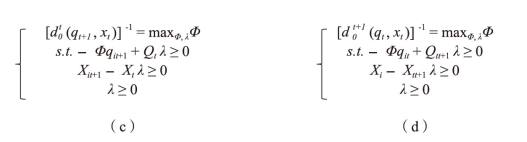
分式（5-10）中，q表示投入向量，x表示产出向量，λ（0＜λ＜1）是一个标量，表示在规模报酬不变条件下，决策单元的技术效率。式（c）和式（d）中，生产点是与不同时期的技术进行对比的，参数Φ不一定像计算Farrell（1957）面向产出的技术效率时那样，必须大于或者等于1。数据点可以位于生产可能集上面。在上述的4个线性规划方程中，参数Φ和λ可能取不同的值。对于样本中的每一个公司，必须解上述的4个方程。如果有I个公司，T个时期，那么要解I×（3T-2）个线性规划方程，因为额外的时间周期添加进来，对于每个公司（为了构造环比指数），必须解额外的3个线性规划方程。例如有30个样本企业，8年的数据，则需要解30×（3×8-2）=660个线性规划方程。

由上述公式可知Malmquist指数描述了企业不同时期的效率变动情况，对其进行分解则可以获得影响其效率变动的主要因素。下面我们以生产型企业为例进行Malmquist TFP指数分解说明，图5-1为一个单投入单产出企业的Malmquist TFP指数分解示意图，如果所有市场中所有企业都按照最优规模经营，则其规模收益不变的生产前沿面为0ATUFR-CRSt或OGP-CRSt+1。

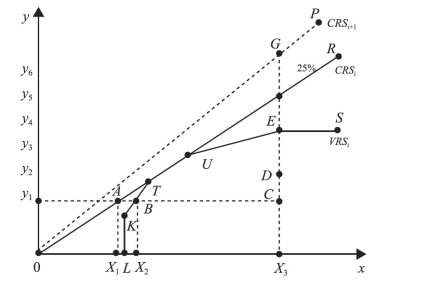
图5-1　Malmquist指数分解图示

由于受到外生和内生等因素的影响，企业将面临规模经济和规模不经济两种可能。Bank等（1984）认为即使是在规模收益可变的情况下，也会有规模收益不变的区域，所以t时期规模收益可变VRSt曲线为LKBTUES-VRSt，该曲线可以看出，在T点左边，规模收益增加；在TU阶段，规模收益不变；在U点右边，规模收益降低。任何企业的前沿面都不是静止不动的，它会随着市场竞争，科技创新，经营管理状态、经济政策及宏观经济形势的变化而变动。

据1957年Farrell关于距离函数的定义和1994年Färe等人关于生产效率的定义，Malmquist全要素生产率指数M是效率改善值（Efficiency Change：EC）与技术进步（Technological Change：TC）的乘积。其中EC代表实际生产情况与前沿面的接近程度，即追赶效应；TC代表在可观测范围内生产前沿面的移动情况，包括技术进步和技术倒退前面的研究中认为成本是已知的，它不只影响到技术效率，而且影响到资源配置效率。如果技术水平的变化引起生产前沿面移动，投入价格降低，将会最终导致总成本下降。不管企业的策略是否建立在平均成本曲线基础上，只有在价格已知的情况下研究技术效率和资源配置效率的变化，对生产效率的提高才有意义。

值得注意的是，企业产出的增加并不能代表其效率得到提高，因为在实际经营中，如果几家企业采用技术革新则会加快行业前沿面的移动，没有进行技术改革的企业则会更加无效。例如在图5-1中，位于C点的企业通过内部挖潜，管理模式的改变等将其经营活动移动到点D，则该企业更有效率，在同样的投入情况下产出增加15%。如果假设t时期的生产前沿面CRSt移动到CRSt+1，技术进步使得大部分企业在同样的投入情况下能够增加产出25%，于是尽管该企业产出增加，仍然技术无效，与生产前沿面相比效率反而下降10%。

（四）分解指数变化对Malmquist指数的影响

由前文可知，根据Malmquist指数计算公式：M=MEC×MTC，M值的变化将受到企业的MEC和MTC影响，Malmquist指数代表了生产效率的变化，表5-1给出了其各种分解指数变化情况的详细信息。

表5-1　Malmquist分解指数对M值的影响

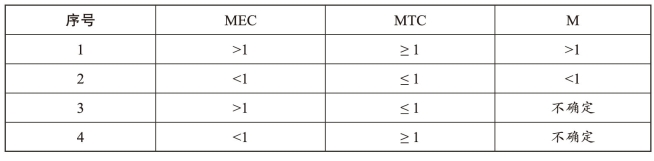
第1种情况是生产效率变化的最优状态，即产出增加的同时，生产前沿面正向移动，技术效率提高，决策单元的M值大于1，生产效率提高。

第2种情形是生产效率变化的最差情况，即企业的产出减少，且生产前沿面朝负向移动，技术效率降低，决策单元的M值小于1，生产效率下降。

第3种情况的生产效率变动结果将不确定。此时尽管决策单元的生产前沿面正向移动，但是技术效率下降，导致决策单元生产效率在t+1时期比t时期远离生产前沿面。当生产前沿面的正向移动大于技术效率下降时，决策单元的M值大于1，生产效率提高；当生产前沿面的正向移动小于技术效率下降时，决策单元的M值小于1，生产效率降低。

第4种情况的生产效率变动结果也不确定。此时尽管决策单元的技术效率有所提高，但是决策单元的生产前沿面负向移动。与t时期相比，t+1时期的生产更靠近生产前沿面。如果生产前沿面的负向移动高于技术效率的提高，决策单元的M值小于1，生产效率下降；如果技术效率的提高超过生产前沿面的负向移动，则M值大于1，生产效率提高。

中国上市公司的货币资金使用效率的变化，受到企业的资金管理技术和资源配置水平的影响，同时也受到企业资金流转效率的影响，前者为企业货币资金使用的技术水平，后者为生产前沿面的移动。接下来，将对中国上市公司的货币资金使用的全要素生产率测度，了解中国上市公司货币资金使用效率变化的趋势，并具体分析导致资金使用效率变化的原因。