1.平稳性检验

为了避免面板数据变量之间经常会发生伪回归现象而造成统计结论失真的结果，本章运用Eviews 6.0计量软件对该模型中的各个变量分别进行ADF单位根检验，检验结果如表5-2、表5-3、表5-4所示。

表5-2　服务业FDI影响因素模型面板数据的单位根检验（全国）

注：“*”“**”“***”分别表示在10%、5%、1%的水平上显著；括号中的数据是该统计量的伴随概率。

表5-3　服务业FDI影响因素模型面板数据的单位根检验（东部地区）

注：“*”“**”“***”分别表示在10%、5%、1%的水平上显著；括号中的数据是该统计量的伴随概率。

表5-4　服务业FDI影响因素模型面板数据的单位根检验（中西部地区）

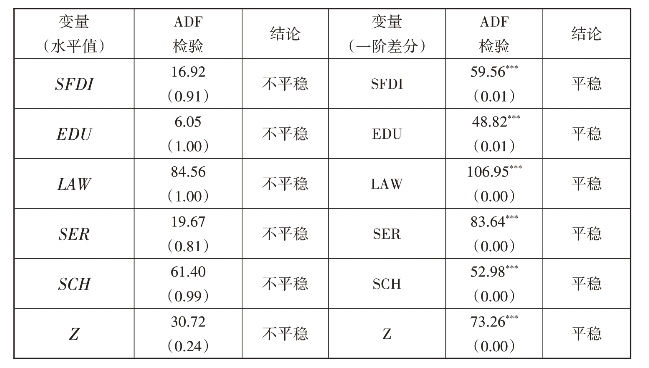
注：“*”“**”“***”分别表示在10%、5%、1%的水平上显著；括号中的数据是该统计量的伴随概率。

根据ADF检验可知，6个变量的水平值均不平稳，而一阶差分在10%的显著性水平之内都是平稳的时间序列数据。所以，原序列是一阶平稳序列，符合协整检验对时间序列同阶单整的要求，能避免产生伪回归的现象。

2.协整检验(www.daowen.com)

面板协整检验的方法有多种，本章则应用Pedroni方法进行分析。通过Eviews 6.0计量软件，面板协整检验结果如表5-5所示。

表5-5　服务业FDI影响因素模型所用变量的面板协整检验

注：1.除了Panel-vstat为右尾检验之外，其余统计检验量均为左尾检验；2.“*”“**”“***”分别表示在10%、5%、1%的水平上显著。

由表5-5结果可知，各个统计量基本上在10%的显著性水平上拒绝“不存在协整关系”的原假设。因此，认为该面板变量的协整关系是成立的，即它们之间存在着一个长期稳定的均衡关系，并可以进行回归分析。

3.回归结果分析

在计量模型的处理上，先利用Hausman检验来判断是采用固定效应模型或者是随机效应模型，使用Hausman检验判断其有效性时，如果Hausman检验值不显著（P＜0.10），则采用固定效应模型，否则选用随机效应模型；接着采用广义最小二乘法（EGLS）进行估计，最终由Eviews 6.0回归的结果，如表5-6所示。

表5-6　服务业吸引FDI的影响因素回归结果分析

注：1.表中括号内为相应系数的t统计值；2.“*”“**”“***”分别表示在10%、5%、1%的水平上显著。

由统计结果表5-5可知，东部地区（模型1）的拟合效果较好，且各个变量在统计上均显著，证明了该模型的有效性。其中，人力资本的回归系数为7.6237，且在1%的水平上显著，这说明当人力资本水平每提高1个百分点，服务业FDI的流入会增加7.6237个百分点，这就验证了假说1；地区法制水平的回归系数为0.8506，且在10%的水平上显著，说明了地区法制水平提高1个百分点，服务业FDI的流入会提升0.8506个百分点，这就验证了假说2；服务业发展水平的回归系数为100.2537，且在1%的水平上显著，这说明了服务业发展水平的提升会较大程度上影响服务业FDI的流入，服务业发展水平提高1个百分点，服务业FDI的流入就会增加100.2537个百分点，这就验证了假说3；劳动力市场化程度的回归系数为358.2292，且在1%的水平上显著，说明了劳动力市场化程度每提高1个百分点，服务业FDI的流入会增加358.2292个百分点，也进一步说明了该因素对服务业FDI流入的促进作用相比其他影响因素更大，这就验证了假说4；政府对经济干预程度的回归系数为-27.9003，这说明了政府对经济的不合理干预会阻碍资源的优化配置，减少服务业FDI的流入，当政府干预经济程度每提高1个百分点时，服务业FDI的流入会减少27.9003，这就验证了假说5。

为进一步验证假设检验的稳健性，本章参照前文的分析方法，将所有的样本数据又分为东部地区和中西部地区两组，根据前面所述方法再次进行回归。从回归结果可以看出，大部分的结论并没有发生实质性的改变，但也出现了些许差别。具体而言，模型2中各个解释变量的回归系数均在统计上显著，且与理论预期一致，而模型3中除了地区法制发展水平回归系数为负值，但不显著，其余解释变量也与前两个模型回归结果基本一致。这说明了我国服务业吸引FDI的有利因素是地区人力资本水平、地区法制水平、劳动力市场化程度、服务业发展水平等，阻碍服务业吸引FDI的不利因素是政府对地方经济干预程度过深。正是这些相关影响因素在地区上的差异，进而影响着服务业FDI地区分布与行业流向上的差异。