根据前文的分析，我们证明了单一的政府补贴、税收政策（无论是比例方式还是总量方式）或者政府持股方式都无法实现帕累托最优的结果，而且解释了无法实现的原因，那么可以实现帕累托最优的政府干预措施就必须同时抑制市场中的企业数量，并增加进入企业的产量，即实现帕累托最优的结果必须是政府限制企业的进入，同时激励已经进入的企业增加生产，那么我们猜测有两个措施可能是可行的实现帕累托最优的方法：

方法1：政府限制企业的进入并持有国有股权，同时对于企业的生产给予比例补贴的支持；

方法2：政府对于进入市场的企业征收一个固定额度的总量税，同时对于企业的生产给予比例补贴的支持。

事实上，通过前文的分析，政府对于进入市场的企业征收总量税的方式等价于政府直接限制企业的进入，相当于提高了企业进入市场的准入门槛，因为当政府向企业征收固定额度的总量税时，只有当企业的利润非负时，企业才会选择进入。那么针对上述两类方法就会产生两个直观的问题：

第一，政府促进已经进入的企业增加产量的措施同为给予比例补贴的方式，而降低市场中企业数量的两个方法（限制进入或者征收总量税）又是等价的，那么这两个方法的区别在哪里？或者方法1 中为何要增加政府持股的干预方式？

第二，是否一个方法可以实现帕累托最优，另一个方法也一定可以实现呢？

首先回答第一个问题。相比于前文的分析，我们在本节判断政府的干预措施是否可以实现帕累托最优时，需要考虑政府预算约束平衡问题，即方法2 中政府从企业征收的总量税即为政府给予企业生产过程补贴的收入来源；而对于方法1，政府给予企业补贴的收入来源缺失，此时我们自然而然就会想到沿用前文的方法，即政府需要通过持有国有股权以获取财政收入来实现预算约束的平衡。因此，两个方法的本质区别在于政府平衡预算约束的方式不同，而正是这一点的差异，导致两个方法并不一定同时实现帕累托最优，这需要后文研究中严格证明。

除此之外，我们需要再次强调，尽管方法1 和方法2 区分了总量税和政府持股，但是这两种方式与本书研究问题的本质是一样的，既不影响企业的生产行为，同时也是政府以国有企业股东身份从企业中获取收益的有效方法，都是国有企业所有制形式的表现。

在本节中，我们的分析思路如下：我们首先在边际成本不变的情况下检验上述两种方式是否可以实现帕累托最优，如果无法实现帕累托最优，我们需要求解出政府的最优干预方式；之后，我们集中讨论企业生产函数时边际成本递增的情况，重复之前的工作，逐一检验不同干预方式是否可以实现帕累托最优，并在此基础上做出比较静态分析。

（1）政府限制企业进入同时持股并给予企业生产比例补贴的方法

根据前文的分析，我们已经知道政府限制企业进入后最优的企业数量应该是1，那么此时政府通过持有国有股权的分红获得了财政收入，可以将这部分财政收入以比例补贴的方式激励企业的生产行为，这与我们在前文中讨论的情况非常相似，但是略有不同。

根据前文的分析，直观想，当企业的成本函数是边际成本不变或是递减时，政府限制企业进入同时持股并给予企业生产比例补贴的方法无法实现帕累托最优；当企业的成本函数是边际成本递增的时候，政府在限制企业的进入后，已进入市场的企业会出于利润最大化选择低于帕累托最优的产量，因此政府对于已经进入市场的企业提供比例补贴的措施可以促进企业的生产、增加产量，同时由于平衡预算约束的方式是政府持有国有股权的分红，源自企业的利润所得，同时政府持股的方式并不影响企业的生产行为（包括企业产出、努力程度等），因此政府对于企业生产行为补贴造成的政府支出总是可以通过持有企业股权、获取分红平衡。因此，政府在满足预算约束情况下给予企业的补贴总是可以带来福利的提升，这与我们在单个企业的完全垄断市场模型中已经证明的结果非常相似。但是，上述分析过程中基于一个重要假设，就是当企业的成本函数是边际成本递增的时候，帕累托最优的结果是最优的企业数量是1，因此才可以得到一个介于0～1 之间的国有股权比例α 的内点解。下文的分析过程将证明，当企业的成本函数是边际成本递增的时候，帕累托最优结果对应的企业数量不再是1，因此关于政府限制企业进入同时持股并给予企业生产比例补贴的方法的分析需要更为严格的证明，我们将在下文中给出证明过程，证明政府最优的干预方式是α=1，但是此时依然无法实现帕累托最优。

（2）政府征收总量税同时给予企业生产比例补贴的方法

对于政府征收总量税的方式，我们在本书中已经讨论过多次，其实质上是提升企业的准入门槛，也就是此时企业进入市场的固定成本从e 提升到e+T（T 为总量税），因此市场中企业的数量会降低，自动抑制了企业进入。我们直观地想，此时抑制企业进入后市场中只存在1 家企业，之后政府再对企业的生产行为进行补贴，比例补贴措施一定可以提升企业的产量，使得原本企业选择生产的垄断产量增加，进而达到帕累托最优的产量。更进一步，由于总量税的方式同样不影响已进入企业的生产行为，那么我们只剩下一个问题，此时政府的预算约束是否可以平衡呢？我们对比方法1，方法1 中政府平衡预算约束的方式是政府通过持有国有股权的分红获取企业的部分利润，并以此补贴企业的生产行为，而总量税的方式可以获取企业的全部利润（比如使得企业是零利润，因此不会再有企业进入），因此如果获取部分利润的持股方式可以实现政府补贴的自给自足，那么总量税的方式一定也是可以的，因此这一方法显然可以实现帕累托最优。

但是，上述的分析中忽略了一个问题，因为存在市场的准入门槛e，因此社会福利水平W(Q )大于0，并不代表企业的利润π 大于0，这个时候如果政府再进一步征收总量税，虽然同时给企业的生产提供比例补贴，但是企业的利润π 有可能小于0，可能就没有企业进入了，也就导致政府的税根本收不上来，因此我们需要考虑到这种情况，所以我们需要证明政府征收总量税后，企业依然有动机进入市场，不然企业就会选择退出。换言之，政府给予企业生产过程比例补贴的补贴率s 是唯一确定的，不能任意改变，我们需要证明：对于政府给定的补贴率s，企业利润π 正好是大于0 的，详细证明请见本章附录。

当企业的成本函数是边际成本递减或是不变的时候，虽然方法1 和方法2 均无法实现帕累托最优，但是我们依然可以计算出政府最优的干预方式，而且是最优平衡干预（即政府预算约束一定是平衡的），这一均衡结果将会尽可能地接近帕累托最优的位置，尽可能地接近最优的产量。

我们以单一产品垄断的情况为例，结合图3.1 阐释我们的思路：图3.1示意的是边际成本不变的情况，分别描述了垄断和完全竞争的结果。垄断情况的均衡点如图3.1 中①所示，而完全竞争（或社会最优）的结果如图3.1 中③所示。垄断企业的利润就是矩形B 的面积，均衡点尽可能往右移，往右移的过程中企业的利润是缩小的，但是通过政府补贴，企业的总利润实际上是在增加，然后政府再通过持股或是征收总量税的方式将企业的利润收回来，虽然政府干预情况的均衡点（②）达到不了社会最优（③），但是政府干预情况下依然存在最优的均衡点，这个位置会尽可能地接近社会最优的均衡点，相比于垄断情况的均衡点（①）存在改进。

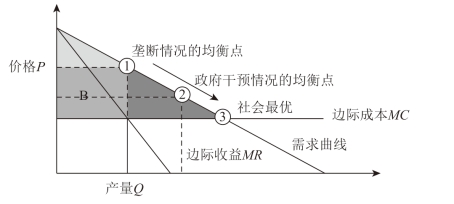
图3.1　政府最优干预方式示意

我们会思考此时政府的权衡取舍是什么：政府给企业提供的补贴越多，企业选择的最优产量越会接近社会最优的点，但是补贴的越多，政府需要从企业获取的利润就越高，以平衡预算约束。但是，当边际成本不变或是递减的时候，越接近社会最优的位置，企业的利润将不足以支撑政府的补贴支出，意味着即使政府获取企业的全部利润并补贴也无法实现社会最优，因此我们猜测，政府的最优持股比例一定是100%持股，即企业的全部利润都被政府索取，所有的收入也都重新补贴给企业的生产，实现最大的补贴力度，政府也没有再多的资金了，政府收入依然不够支撑补贴支出，所以无法实现社会最优。因此，当边际成本不变或是递减的时候，由于预算约束永远是紧约束，所以政府必须100%持股，只有这样，才可能最大程度接近社会最优的点。

上述只是经济学分析，还需要经过严格的证明，才可以得出结论。首先，我们证明方法1 中政府最优的干预方式是最优持股比例α=1。

由政府的优化问题，得到：

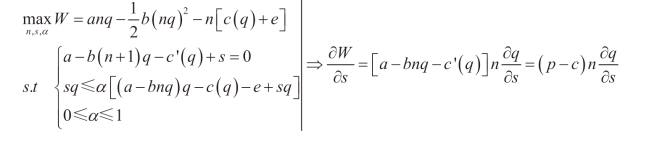
回到企业的优化问题，得到：

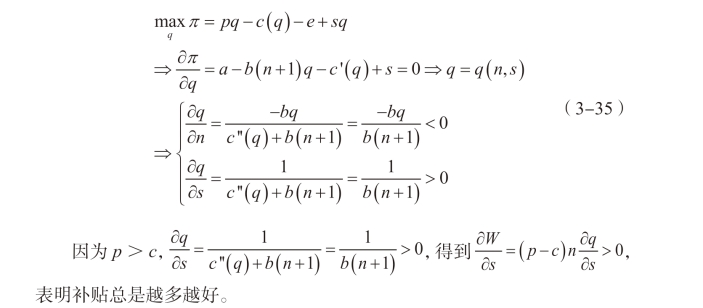
由于补贴的收入来源完全来自政府持股获取的企业利润分红，企业的全部利润用于补贴支出最优，故政府最优的干预方式是α=1。

虽然证明了方法1 中政府最优的干预方式是最优持股比例α=1，但是还需要将方法1 和方法2 干预方式下的福利水平进行比较，比较哪一种方式的均衡结果更接近帕累托最优。

我们首先计算政府持股比例等于1 情况下的社会福利水平。

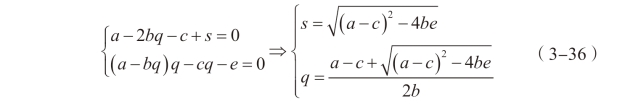
此时社会福利水平为：

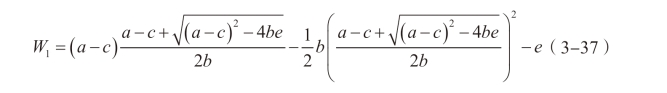
接下来，我们计算方法2（政府征收总量税同时给予企业生产比例补贴的方法）干预方式下的社会福利水平。

联立企业的一阶条件和零利润条件，得到：

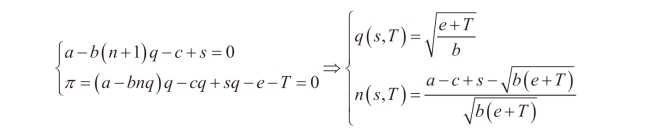
根据政府的平衡预算约束条件得到s=s(T )：

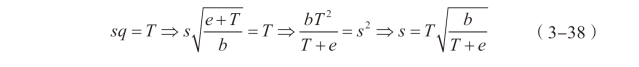
将q=(s,T )，n=(s,T )，s(T )代入政府的优化问题中，得到：

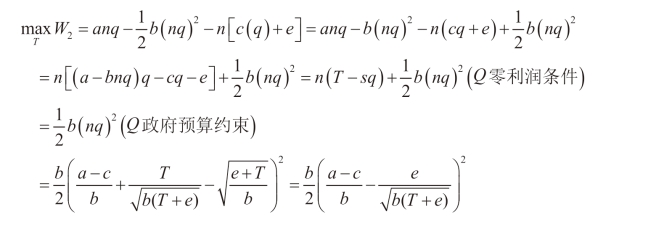
由此可知，社会福利水平W 是T 的单调递增函数。

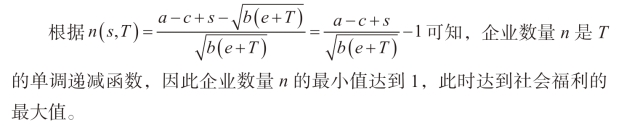
根据企业零利润条件得到：

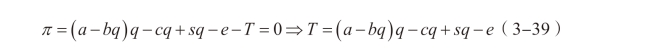
进而根据政府的平衡预算约束条件得到：

此时社会福利水平为：

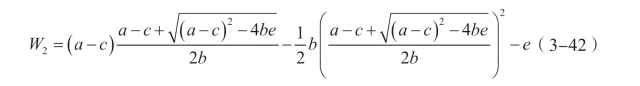
由W1=W2，我们严格证明了，两种干预方式下社会福利水平是相同的，再次反映出政府征收总量税与政府持股在本书研究问题中的本质是相同的。

至此，围绕本节的研究问题，我们已经完成对于企业生产函数是边际成本递减或不变情况的分析，之所以不同干预方式都无法实现帕累托最优，原因在于政府受限于预算约束平衡条件、无法提供企业生产足够多的补贴，换言之，如果政府有足够多的可支配收入或者额外的收入可以用于补贴企业的生产，上述两种干预方式（政府限制企业进入同时持股并给予企业生产比例补贴的方法，政府征收总量税同时给予企业生产比例补贴的方法）是有可能实现帕累托最优的。

事实上，假设企业生产过程中的边际成本是常数的情况，即可变成本函数是线性函数的形式，这只能够代表部分企业的特点，实际情况中，随着产量的变化，企业的边际成本并不都是常数，可变成本也不再是线性变化，边际成本的改变会影响平均成本，比如存在企业的管理成本，当一个企业的产量过大时，企业的管理成本会激增，此时多个企业的管理可能是有利的。换言之，如果多个企业管理成本的节省可以抵消多个企业准入成本增加带来的负效应，那么此时政府最优的选择可能就不再是简单的完全垄断，这就是我们接下来即将分析的问题，即企业边际成本不再是常数的情况。为了与前文模型区分，下文建立模型的所有变量均用下脚标4 表示。

对比式（3-17）可以看到：当边际成本不再是常数的时候，社会福利水平的表达式中，只有消费者剩余部分与企业数量无关，第二项可变成本和最后一项准入门槛相对应的固定成本项均与企业数量有关，而且这两项随着企业数量增加的变化方向并不一定一致，因此我们无法得出固定成本总是越低越好的结论，因此此时帕累托最优的结果不一定是极端情况下完全垄断市场的结果，我们通过下述计算可以得到更为清晰的认识。

通过计算可以解得帕累托最优的企业数量，此时帕累托最优产量Q4*是给定的：

(www.daowen.com)

综上所述，我们得到定理6：

【定理6】

对于一个允许企业自由进入但是存在准入门槛的寡头垄断市场，当企业生产的边际成本递减或为常数时，帕累托最优的企业数量是1；当边际成本递增时，帕累托最优的企业数量不为1。

当然，造成帕累托最优的企业数量不为1 的原因有很多，一方面是基于边际成本的考虑，即我们这里已经证明的结果；另一方面可能是基于产品多样性的考虑，这是我们在第4 章中需要分析和讨论的内容。

（1）比较静态分析

我们首先考虑帕累托最优对应的企业数量n4*随市场准入门槛e 的变化。

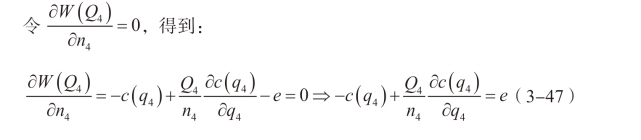
（3-47）等式两边同时对e 求导，得到：

（2）政府干预是否可以实现帕累托最优

当成本函数c(q4)是边际成本递增时，我们重复之前的工作，即分别证明下述方法是否可以实现帕累托最优的结果，其中方法1 至方法4 是单一的干预方式，方法5 和方法6 是组合的干预方式：

方法1：单独给予企业生产过程比例补贴（Proportional Subsidy）；

方法2：单独对于企业生产过程征收比例税（Proportional Tax）；方法3：单独给予企业生产过程总量补贴（Lump Sum Subsidy）；方法4：单独对于企业生产过程征收总量税（Lump Sum Tax）；

方法5：限制企业的进入，同时给予企业生产过程比例补贴，但是为了平衡政府的预算约束，政府通过持有国有股权的分红获得财政收入；

方法6：政府对于企业征收总量税，同时对于企业的生产过程提供比例补贴。

参考前文的研究思路，我们依然首先求解考虑帕累托最优的结果。此时，政府的优化问题为：

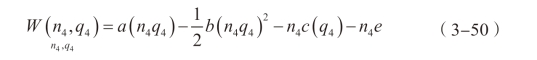
政府优化问题的一阶条件得到：

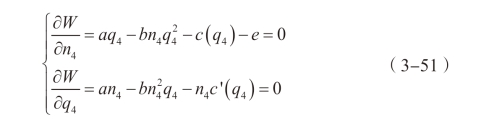
因为比例补贴与比例税收互为相反过程，因此我们将方法1 和方法2合并在一起讨论。

回到企业的优化问题，此时第i 个企业的优化问题是选择自己的产量以最大化企业的利润：

由企业同质性，我们对于企业优化问题求一阶导，得到单个企业的产量满足的条件：

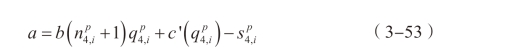
由n 个企业的一阶条件结合对称性，可以推出每个企业的产量相同。

我们将式（3-53）代入企业的利润表达式，并根据企业停止进入市场的零利润条件，得到：

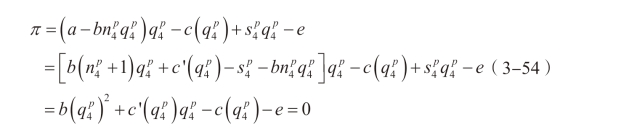
由反证法证明可知，方法1 和方法2 均无法实现帕累托最优，详细证明过程请见本章附录。

接下来，我们讨论方法3 和方法4。因为总量补贴与总量税收互为相反过程，因此我们将方法3 和方法4 合并在一起讨论。

回到企业的优化问题，此时第i 个企业的优化问题是选择自己的产量以最大化企业的利润：

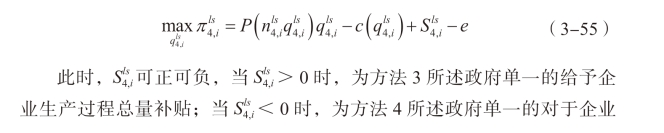
由企业同质性，我们对于企业优化问题求一阶导，得到单个企业的产量满足的条件：

由n 个企业的一阶条件结合对称性，可以推出每个企业的产量相同。

我们将式（3-56）代入企业的利润表达式，并根据企业停止进入市场的零利润条件，得到：

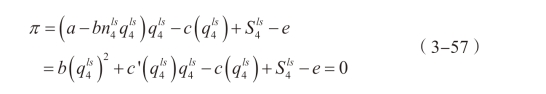
由反证法证明可知，方法3 和方法4 均无法实现帕累托最优，详细证明过程请见本章附录。

经过上述证明，方法1 至方法4 均无法实现帕累托最优，那么将补贴政策、税收政策和政府持股等不同干预方式组合而得的方法5 和方法6 是否可以实现帕累托最优的结果呢？

方法5 描述的是：政府限制企业进入，同时给予企业生产过程比例补贴，但是为了平衡政府预算约束，政府通过持有国有股权的分红获得财政收入。

第i 个企业的优化问题是选择自己的产量以最大化企业的利润：

由企业同质性，我们对于企业优化问题求一阶导，得到单个企业的产量满足的条件：

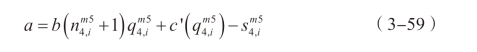
由n 个企业的一阶条件结合对称性，可以推出每个企业的产量相同。

由反证法可知，方法5 可以实现帕累托最优，详细证明过程请见本章附录。

最后检验方法6。方法6 描述的是，政府对于企业的生产征收总量税，同时对于企业的生产过程提供比例补贴。

第i 个企业的优化问题是选择自己的产量以最大化自己的利润：

由n 个企业的一阶条件结合对称性，可以推出每个企业的产量相同。

由反证法可知，方法6 也可以实现帕累托最优，详细证明过程请见本章附录。

与方法5 相似，我们同样需要增加边界限制条件，即行业的固定成本e 不能非常大，此时方法6 才可以实现帕累托最优的结果。