6.4.3.1 算法流程

非支配排序遗传算法（Non-dominated Sorting Genetic Algorithm，NSGA）是于20世纪90年代由N.Srinivas和K.Deb提出的基于个体等级分层的遗传算法，NSGA把多目标简化至一个适应度函数，已成为目前解决多目标问题最常用的方法之一。印度科学家Deb对NSGA进行了改进，提出了基于快速非劣性排序的NSGA-II方法^[66]，它用拥挤距离估计某个点周围的解密度取代适应值共享。本书在传统NSGA-II的基础上，结合拟解决的问题，对NSGA-II在本课题中的应用进行了改进，设计了自适应NSGA-II算法（Adaptive Non-dominated Sorting Genetic Algorithm，A-NSGA-II），其算法流程与改进措施如图6-14所示，主要改进措施包括：

（1）针对拟解决的问题，采用多层染色体编码设计实现产品服务工程师的协同作业。

（2）针对实际问题的目标特性，引入了自适应拥挤距离计算方法减小由于两个目标的理想值差异巨大对个体适应度的评判带来的影响。

（3）为了更好地选出最优个体，采用了多属性个体排序规则以体现实际决策中不同目标重要性有差异的特性。

（4）为了防止早熟和提高后期搜索效率，采用了自适应锦标赛选择机制。

（5）为了防止非法个体的产生，设计了组合交叉算子和组合变异算子。

图6-14 A-NSGA-II算法流程与改进措施

6.4.3.2 多层染色体编码设计

为了准确表达不同小组产品服务工程师的协同作业关系，本书在分段染色体非负整数编码技术的基础上^[67-68]，采用了多层染色体编码设计和实数编码方式，每个染色体包括多个子染色体，每个子染色体表示一个技能小组。同时，为了恰当描述每个产品服务工程师工作的相对独立性和工作路径的随机性，每个子染色体包括三部分：第一部分为工程师随机排列序列，第二部分为客户点随机排列序列，第三部分为客户点分割序列。这里以两个技能小组（机械组和电气组），每个小组由m个工程师、n个客户点的工程师配置优化为例，该问题的染色体编码如图6-15所示，该染色体共包含2（m-1+n）个元素，其中每个子染色体的客户点分割序列的长度为（m/2-1），客户点分割序列指出了每个产品服务工程师的工作路径。

如无特殊说明，本小节的示例取m=5和n=60。假设某子染色体为[21 3|45327①⑥|25]，它表示该方案中共有3个产品服务工程师、7个客户，其中客户被分为三个组：第一组包括客户4和5，由工程师2依次为其提供服务；第二组包括客户3、2和7，由工程师1依次为其提供服务；第三组包括客户1和6，由工程师3依次为其提供服务。

如果在客户点序列中某元素值为0，这表示经过该路径的产品服务工程师不访问任何客户，如图6-15所示，假设客户点37、0和15在同一个产品服务工程师的路径上，那么该工程师从客户点15离开后直接访问客户37。如果不同子染色体中客户点序列的元素值相等，则说明不同技能小组的产品服务工程师将协同为同一客户提供产品服务。

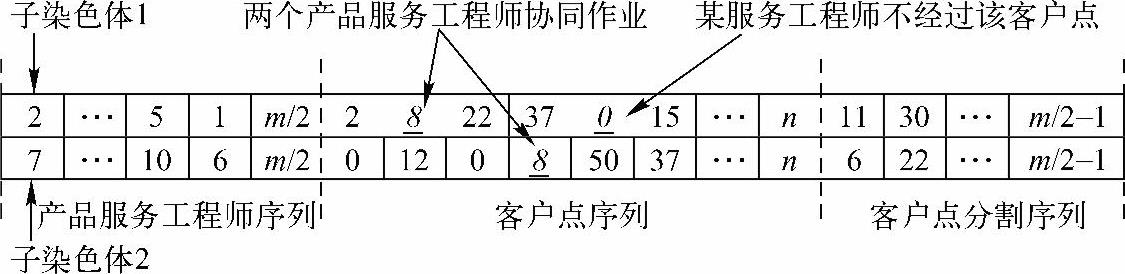
图6-15 染色体编码示例

此外，如果多个小组的工程师数量不相等，则用0来填补工程师序列和客户点分割序列，如图6-16所示。在解码时0并没有实际意义，在交叉和变异中0值不参与操作。

图6-16 多小组且工程师数量不等时的染色体编码示例

6.4.3.3 染色体解码

由于本书采用的是实数编码，并且同一组的产品工程师不允许经过同一个客户点，即如果有两个工程师服务于同一个客户，只能是来自两个技能小组。多工程师协同作业环境下染色体的交叉和变异操作比较复杂，算法采用的染色体解码流程如下：

（1）对于任一个客户点，首先扫描该客户点是否有另外一组的工程师经过，如果无，判断这个工程师是否有能力胜任该客户的所有作业：

1）如果胜任，st_i=at_ei。

2）如果不胜任，则此工程师到达该客户点后立即离开，即在此停留时间为0，但是旅行时间要计入总时间，此时认为该客户的产品服务任务未能完成，则在该“染色体”解码出的“总体客户满意度”目标函数施加一个惩罚项。

（2）如果有多个工程师经过该客户点，判断这些工程师是否有能力胜任该客户的某一作业：

1）如果该客户有一个作业所有的工程师都没有能力完成，则所有的工程师到达后（同时）立即离开，即在此停留时间为0，但是旅行时间要计入总时间。此时认为该客户的服务任务未能完成，则在该“染色体”解码出的“总体客户满意度”目标函数施加一个惩罚项。

2）如果该客户的所有产品服务作业都可以被完成，则这些产品服务工程师开始协同作业：

➢计算所有产品服务工程师的到达时间，以最晚到的产品服务工程师的到达时间为开工时间：st₁=max{at_e1i，at_e2i}

➢按照胜任原则为到场工程师分配任务，胜任的原则是工程师可以胜任分配的作业，同时客户的作业都能被完成。

➢计算所有人的耗时，以耗时最长的时间为客户的服务耗时，也就是ct_i=max{at_1i，at_2i，…，at_si}+max{st_1i，st_2i，…，st_si}。此时如果某一个产品服务工程师不胜任任何作业或者没有分配到任务，该工程师也要和其他人一起离开（等到全部作业完成后）。

6.4.3.4 种群初始化

首先随机生成每个子染色体的产品服务工程师序列和客户分割点序列，其中客户点分割序列的元素值应该是逐渐增大的。然后生成每个子染色体的客户点序列，客户点序列生成遵循如下规则：

步骤一：随机生成子染色体1的客户点序列的元素值，且元素值不重复，取值范围为[1，60]。

步骤二：把其他子染色体的客户点序列的元素值置为0。

步骤三：随机选择子染色体1的客户点序列的部分元素值赋给同位置的子染色体2的元素。（如果有多个子染色体，则从子染色体1的客户点序列剩余的元素值中选择部分赋给同位置的子染色体3的元素，以此类推，直到所有的子染色体客户点序列生成完毕）。

步骤四：把子染色体1中那些被赋给其他子染色体客户点序列的元素的值全部置为0。

对于包括多个子染色体的个体而言，同样依照上述步骤进行，只是每次从第一个子染色体中不重复地复制相同数量的元素值到其他自染色体上，因此，初始化之后的染色体具有每个客户点只有1个产品服务工程师经过的特点，如图6-17所示。

图6-17 染色体初始化示例

6.4.3.5 自适应拥挤距离计算

为了便于观察和比较个体排序输出结果，需要把式（6-6）调整为

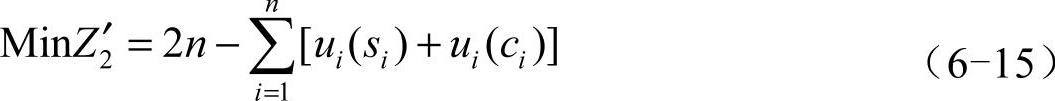
这里n是客户点的个数，把式（6-3）和式（6-15）作为计算个体目标函数的计算依据。

等级排列是NSGA-II算法的一个基本特征，它按照个体在种群中被支配的程度进行排序。在图6-18中，实心点是当前的帕累托前沿，其等级为1，空心点个体的等级为2。个体等级越低，说明该个体越接近真正的帕累托前沿，而拥挤距离用来衡量处在同一等级上个体的优劣程度。常用的拥挤距离计算方法如图6-18所示，即目标空间第i点的拥挤距离等于它在同一等级相邻的点i-1和i+1组成的矩形2个边长之和（a+b）。但是，这种方法忽略了各个目标在数量级上的较大差异，因而，本书设计了考虑空间上的欧式距离的自适应拥挤距离计算方法：(www.daowen.com)

式中d_i—个体i的拥挤距离；

是由等级为1的边缘个体解码得到的。

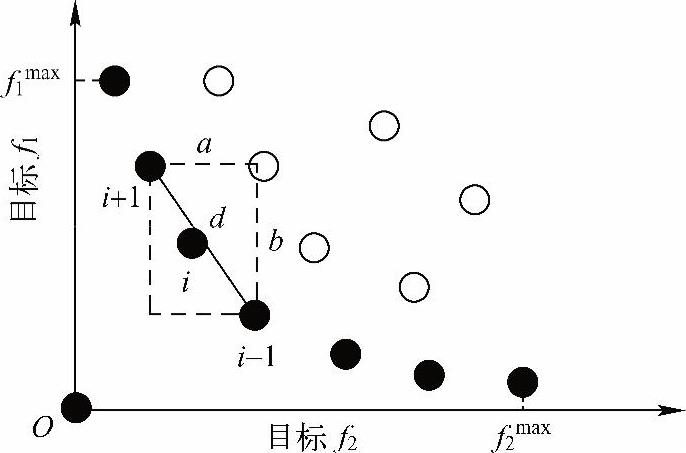
图6-18 个体的拥挤距离

6.4.3.6 多属性个体排序规则

经过个体排序和拥挤距离计算，可以得到个体i的三个属性：非支配排序等级r_i、拥挤距离d_i和个体在多个目标函数上的排序等级。这三个属性构成个体进化的选择依据，也就是：首先优先选择级别低的个体；其次考虑个体的拥挤距离，给予拥挤距离大的个体较多的参与进化的机会，以维持种群的多样性；最后考虑个体在多个目标函数上的排序等级，也就是如果两个个体的排序等级和拥挤距离都相等，则按照多个目标函数的重要程度不同，优先选择在重要目标函数上排序等级低的个体。

6.4.3.7 自适应锦标赛选择机制

锦标赛选择通过每次从若干个个体中选择适应度最高的个体参与遗传操作，具有随机性强、最优个体选中率高、最差个体淘汰率高的特点。锦标赛选择的参数竞赛规模Tour直接影响多样化损失，竞赛规模Tour与多样化损失的关系如式（6-17）所示，可见，选择强度越大，多样化损失越严重，Tour=10的时候多样化损失约为70%，但是优良基因得到重组的机会越大，进化速度越快，最优个体可以快速向真正帕累托前沿移动，同时较大的选择强度也限制搜索空间。选择强度越小，多样化损失越小，虽然进化速度越慢，但可以对搜索空间进行有效广度搜索。

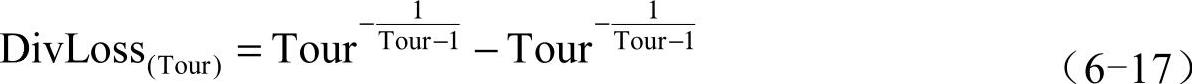
为了在进化初期采用较小的选择强度和在进化后期获得较大的选择强度，本书采用了自适应锦标赛选择机制，见式（6-18），竞赛规模随种群进化的变化如图6-19所示。

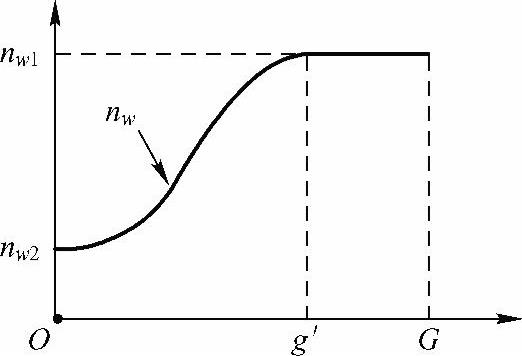
图6-19 自适应竞赛规模

式中 G—最大进化代数；

g—当前进化代数；

g'—选择压力不再变化的进化代数，进化代数大于g'后竞赛规模不

再变化；

nw—当前竞赛规模；

n_w1和n_w2—最大和最小竞赛规模，其中nw2≥nw1≥2，nw2≤n；

n—种群大小。

6.4.3.8 组合交叉算子

根据染色体编码方案，为保证染色体结构的完整性以及对应解决方案的准确性，交叉操作需要分层并分段交叉，这里采用产品服务工程师序列、客户点序列和客户点分割序列分别操作的组合交叉策略。

对于产品服务工程师序列的交叉，采用两点交叉方式，交叉即在对方的母体中消去被选择部分的元素值，然后将被选择部分补在对方的子染色体之后，详细步骤如图6-20所示。

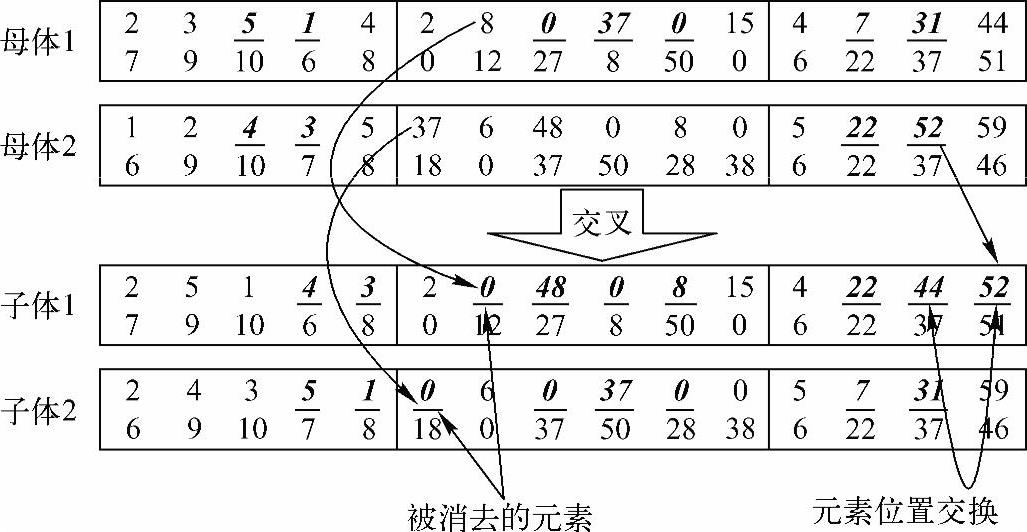
图6-20 交叉操作示例

步骤一：随机选择一个子染色体，并随机选择两个交叉点，把交叉点之间的部分作为交换对象。

步骤二：如果对方的母体中含有被选择部分的元素值（除0外），首先从对方母体中消去该元素值。例如图6-20中，母体1中被选择的部分为5和1，则需要从母体2中消去这两个值，此时母体2的服务工程师序列变为了[243]。

步骤三：把剩余的元素依次左移，以母体2为例，此时服务工程师序列变为了[243]。

步骤四：把被选择部分的元素补在对方母体的服务工程师序列的尾部，仍旧以母体2为例，此时其服务工程师序列变为了。

对母体1同样也进行如上操作，最终实现染色体客户点序列的交叉操作。

客户点序列的交叉操作同样采用两点交叉，如果对方的母体中含有交叉点之间的元素值（除0外），首先从对方母体中消去该元素值，然后交换被选择部分的元素值；如果对方的母体中不含有交叉点之间的元素值（除0外），则直接交换被选择部分元素值。

客户点分割序列仍然采用两点交叉，但是交叉后需要对染色体进行修复以避免非法个体的出现，即如果客户点分割序列中前一个元素值大于后一个元素值，需要把元素值较大的元素与后一个元素的位置依次互换，直到任何两个相邻的元素中前一个元素值都不大于后一个元素值为止。假设图6-20的子体1的客户点分割序列交叉操作后变成了，通过染色体修复则变为了。

6.4.3.9 组合变异算子

同交叉操作一样，针对染色体的不同部分采用不同的变异操作。对产品服务工程师序列的变异采用基因交换算子，即随机选取子染色体上若干对元素，两两随机交换位置，如图6-21所示。

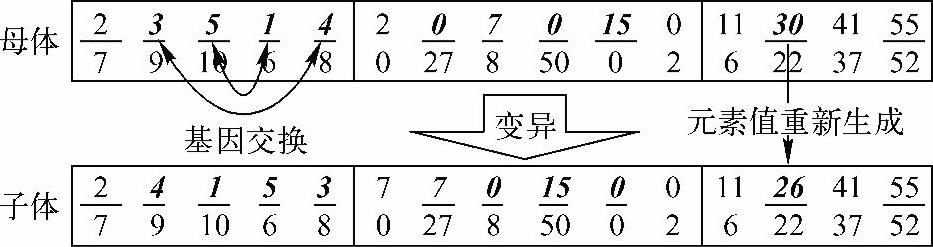
图6-21 基因变异操作示例

客户点序列的变异采用基因交换算子和基因插入相结合的方式，基因交换算子操作同上，基因插入操作流程如图6-22所示。

对客户点分割序列的变异采用元素值重新生成的方法，即直接把元素值随机修改为前后两个分割点值之间的任一正整数，如图6-21所示，假设30是被选定的元素，则需要把30修改为10和41之间的任一正整数。如果被选择的元素位于客户点分割序列首位，即选定元素为11，则需要把该元素修改为0和30之间的任一正整数；如果被选择的元素位于客户点分割序列尾部，即选定元素为55，则需要把该元素修改为41和60之间的任一正整数。

图6-22 基因插入操作流程