网络层中元素的权重是通过求解加权超矩阵得到的。通过对群决策判断矩阵的一致性检验和修复，所有的判断矩阵具备了进一步处理的条件。求出元素组T_i中的元素t_in对元素组T_j中tjm影响的判断矩阵的特征向量并归一化，可以得到Ti中的元素t_i1，t_i2，…，tin对元素组Tj中tj1，tj2，…，tjm的影响程度排序向量，也就是W_ij中的列向量（见式（4-16））。若T_j中的元素不受T_i中的元素的影响，则W_ij=0。计算所有元素相互影响的权重向量，可以得到在控制元素下的超矩阵（见式（4-17））。

超矩阵的每一个元素都是一个矩阵，并且子矩阵的列和为1，但是，该超矩阵并不是归一化矩阵。因此，求出在“服务供应商选择评价”准则下的网络层元素组T_i的重要性判断矩阵的排序向量并归一化，经过解模糊化可以得到常规加权矩阵：

把加权矩阵A与超矩阵W相乘得到加权超矩阵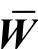：(www.daowen.com)

加权超矩阵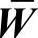的元素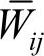即反映了网络层元素的相对优势度。归一化加权超矩阵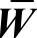后，各个元素的相对重要性可以通过计算极限相对排序向量获得：

如果极限值存在且唯一，这时得到的W∞各行的非零值均相同，W∞的第j列就是网络层中各元素对j对应元素的极限相对排序向量，进而可以求得目标准则下网络层中所有元素的相对权重ω=（ω₁₁，ω₁₂，…，ω₆₃）T。