1.一致性检验

为了便于构建超矩阵并判断和修复判断矩阵的一致性，首先需要对模糊判断矩阵进行解模糊化，同理，在计算模糊判断矩阵的特征向量时也需要把其转化为常规矩阵，下文不再赘述。常用的解模糊化的方法包括重心法、α截集法、平均值最大法、面积重心法等。考虑到方法的实用性和计算的简洁性，本书采用重心法进行解模糊化：

对判断矩阵的一致性进行检验时，指数标度的随机一致性指标（Random Consistency Index of the Geometric Scale，RIG）的取值参照表4-5^[54]，判断矩阵的一致性指标（Consistency index，CI）和一致性比例（Consistency Ratio，CR）计算可以分别参照式（4-5）和式（4-6）计算，其中γ_max是判断矩阵的最大特征变量，n是矩阵的维数。如果CR小于0.1，则说明判断矩阵一致性是可接受的，反之，则需要对群决策判断矩阵进行修复。

表4-5 指数标度的随机一致性指标

2.随机一致性修复

尽管采用指数标度可以改善判断矩阵的一致性，在多个决策者参与的服务供应商选择之中，总是会存在某个决策者的判断矩阵无法满足一致性要求的情况，特别是判断矩阵的维数比较高时。但是，如果直接对每个不符合一致性要求的判断矩阵单独进行修复，每次修复都会无法避免地导致部分决策信息的丢失，修复的次数越多，决策信息变异越大。同时，虽然个别决策者得出的判断矩阵的一致性不满足要求，但是群决策判断矩阵仍然有可能是可接受的。本书提出的群决策判断矩阵修复方法是通过基于原始判断矩阵构建完全一致性正反互补判断矩阵，然后通过构建的矩阵与原判断矩阵进行叠加获得一系列替代矩阵，最后计算替代矩阵与原始判断矩阵特征向量之间的欧式距离，距离最小者对应的矩阵即为最佳替代矩阵，详细流程如图4-5所示。

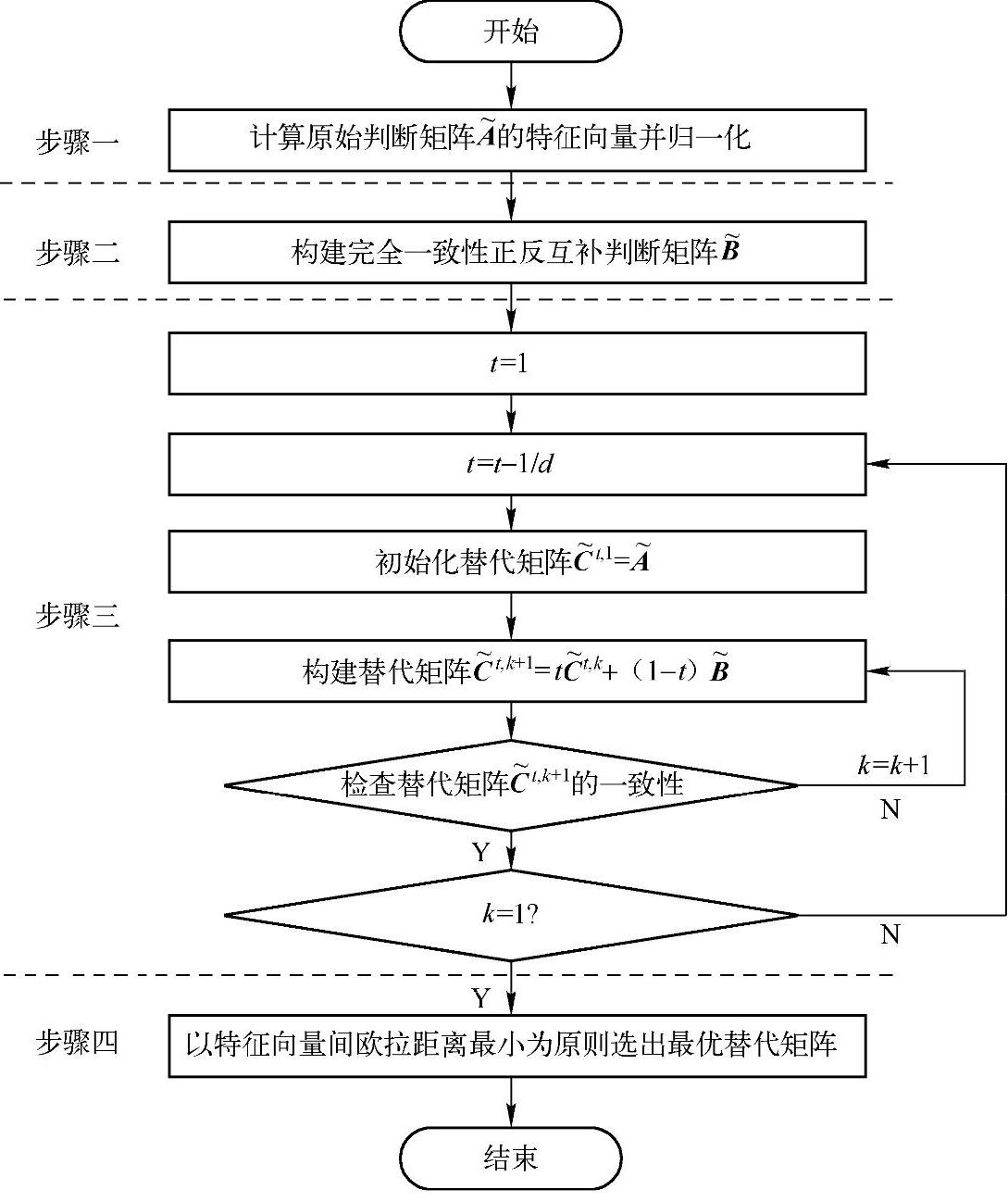
图4-5 判断矩阵一致性修复流程

步骤一：通过式（4-7）和式（4-8）计算原始判断矩阵（常规矩阵）的特征向量ω，并对ω进行归一化处理。

步骤二：参照式（4-9）构建完全一致性正反互补判断矩阵：[55]

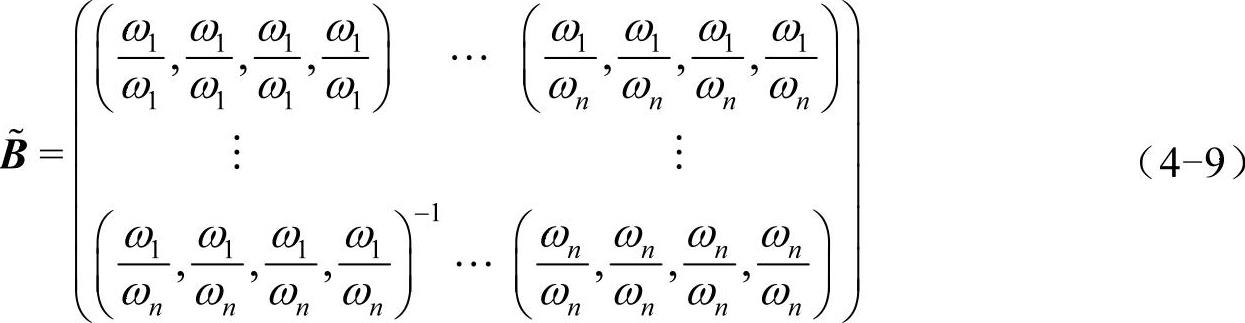
步骤三：通过原始判断矩阵和完全一致性正反互补判断矩阵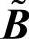的线性组合构建替代矩阵，如式（4-10）所示。(www.daowen.com)

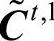但是，对于不同的t可以得出不同的替代矩阵，对于任一值t，替代矩阵的初始值为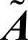，经过k次迭代后的替代矩阵为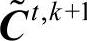，可以得到一系列满足一致性要求的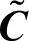，其表达式如式（4-12）所示，式（4-13）给出了其具体形式。

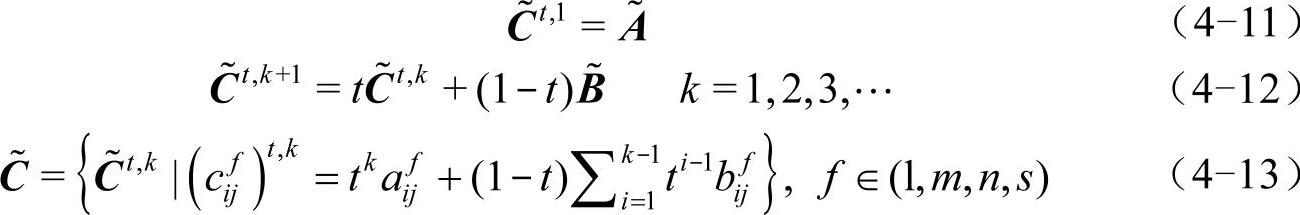
原始判断矩阵包含极其丰富的原始决策信息，但是：

●式（4-10）表明，t越小，构建的替代矩阵继承的原始决策信息越少。

●式（4-13）表明，对于同一个t，迭代次数越多，也就是k越大，构建的替代矩阵继承的原始决策信息损失越多。因而：

●对于同一个t而言，一旦通过式（4-12）计算出的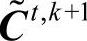符合一致性要求，就没有必要再循环计算下去（k继续增大）。

●对任一t而言，一旦k=1时得到的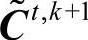满足一致性要求，也没有必

要再循环计算下去（t继续减小）。

为了使构建的替代矩阵尽可能多地保留原始决策信息，t变化的步长d应该尽可能小。

步骤四：以特征向量欧式距离最小为原则选出最优替代矩阵。首先计算符合一致性要求的替代矩阵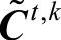的特征向量ω^t，k，然后逐一计算ω^t，k与原始判断矩阵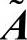的特征向量之间的欧式距离，具有最小欧式距离的ω^t，k对应的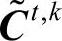即为最优替代矩阵：

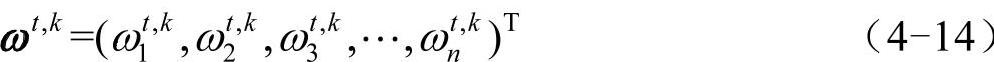
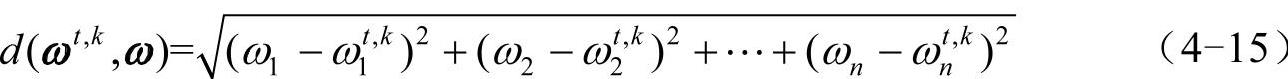
就ANP方法的原理而言，判断矩阵的决策信息最终是以特征向量的形式表现出来，同时，判断矩阵的特征向量也是构建超矩阵的基础，替代矩阵的特征向量与原始判断矩阵的特征向量的欧式距离越大，说明决策信息的变异越大，反之，说明决策信息的变异越小。因而，通过上述方法得到的替代矩阵是最能够准确反映决策者的判断的矩阵，并把决策信息客观地保留下来。