结合问题的基本性质和决策支持要求，本书改进了多目标优化环境下的适应度函数设计方法，采取基于个体排序和目标函数权重因子相结合的个体适应度计算方法，既考虑目标函数权重又可避免目标函数极值的影响，还可以优化算法的收敛速度。

假设目标函数为Z_（^′_x），每个个体都会按照对其目标函数为Z_（^′_x）的优劣生成一个可行解的排序序列x_i（即第i个目标函数，i=1，2，3，…，n，n为目标函数总数）。在所有个体对每一个目标都排序后，就可以得出个体对所有目标函数的总体表现。根据个体的排序计算其适应度：

式中

N——种群大小；

X_j——种群的第j个体；

Y_i（X_j）——个体Xj对目标i的优劣排序后所得的序号；

g——迭代次数（又称进化代数）；(www.daowen.com)

G——最大迭代次数；

F_i（X_j）——X_j对目标i所得的适应度；

F（X_j）——X_j考虑全部目标函数值后得到的总适应度；

αi——第i个目标的权重。

系数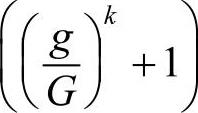用于加大优良个体的适应度函数值，理论上k是（1，∞）上的实数。

在进化初期，最优个体与其他个体的适应度值差别不宜太大，防止过快收敛到局部最优解；进化后期对应的最优个体的适应度与其他个体的适应度应该加大，以提高收敛速度。