遗传算法的提出最初是用来解决无约束规划问题，对约束规划问题常常采用罚函数法。本问题中，除了约束（1）和（4）外，其他约束条件都可以通过染色体实数编码满足，因此，只需要对不满足约束（1）和（4）的个体的适应度值增加一个惩罚项即可。首先把约束（1）、（4）转化为标准形式：

g_i（x）≤0 （3-11） 设p（x）为惩罚函数，则由于个体不满足约束条件i而引入的惩罚项的基本形式如下：

c、ϕ、ω是常数，g是进化代数，一般取c=0.5，ϕ=2，ω=2。考虑到染色体解码得到的解决方案会有多个产品服务中心违反其能力约束（假设共有u₁个）和多个客户点与其对应的产品服务中心的距离违反距离约束（假设共有u₂个），则该个体总的惩罚项为(www.daowen.com)

此时，引入自适应罚函数后个体的目标函数为Z₁′_（x）和Z₂′_（x）如下：

Z_1（x）和Z_2（x）为原目标函数，系数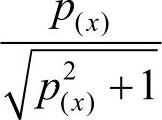可以避免由于目标函数与罚函数值之间的值差距过大影响对个体适应度的判断；p（x）反映了方案违反约束的深度，即个体在多大程度上违反了约束条件；而系数（u₁+u₂）反映了方案违反约束的广度，即个体在多大范围内违反了约束条件，如果一个方案违反约束的次数比较多，例如很多客户点与其对应的服务中心之间的距离都超过了允许值，那么该方案的质量就比较差，其染色体携带优良模式的概率也就比较小。