自欧文·费雪教授的《货币购买力》于1911年出版以来，书中提出的著名方程式PT=MV在世界范围内一直占据着领先地位。这个公式对货币理论的进步发挥了非常重要的推动作用，而我们这些在此基础上成长起来的人，就算发现这一公式无法满足我们的分析要求，也不能认为我们对费雪教授不心怀感激。[49]

这个公式的出发点既不是收入相对于消费品的流动，也不是实际余额，也不是以现金持有的资金比例，而是现金交易总量，或者费雪教授所说的“支出”。令一定时期内现金交易总量为B，现金流通量为M，在此期间，一个单位现金用于交易的平均次数，也就是流通速度为V，则根据定义B = MV。

但我们也可以用不同的方法来分析B。每笔交易都是一定数量的商品、服务或证券乘以该物品的价格。也就是B=∑prqr，其中q是交易数量，p是交易价格。以基准年一个单位值的金额作为数量单位。可得

B=∑prqr=P2T

其中

亦可理解为：P2是交易商品的物价水平，单个商品价格按其货币交易量的比例进行加权，也就是说，P2衡量的是第6章所界定的现金交易标准；T是交易单位总数（任何东西的单位都是指在基准年一个单位货币对应数量），按其相对价格比例进行加权，即按相关年份用P2计算的价格比例进行加权，也就是说，T衡量的是费雪教授所说的贸易量。因此标准的公式是

P2·T=M·V[50]

这一方程式的一大优点在于，M·V这一边，比大多数方程式更符合实际可用的银行统计数字。因此，在定量研究方面，这个方程式比任何其他方程式都有可能取得更大进展。M·V差不多相当于银行票据交换量[51]，M相当于储蓄量，已知这两个数值可推算出V的值。

但是，其不足之处在于，方程式的另一边P2·T。因为无论是P2还是T，都不符合我们所要讨论的量，P2不是货币购买力，T也不是产量。事实上，费雪教授并没有忽视这些不足之处，但我认为他并没有把这些看得太重。他采用近似方法来估计这两个值，这一点也不能令人信服。例如，他试图把批发标准、工资标准和包含40种商品的指数结合起来得出P2的值，其中批发标准权重为30，工资标准权重为1，物价指数权重为3。当然，这是一种开创性的方法。我们现在可以计算出更为精确的P2，而斯奈德先生已经这么做了。但是，我们计算得越精确，就越清楚现金交易标准就是大杂烩，也就越清楚用它来衡量货币购买力有多不可靠。

另一个反对费雪方程式的原因是，它没有明确考虑到活期存款和储蓄存款之间的区别，以及透支的使用，在应用于英国银行业统计时尤其如此。这些因素的潜在变化可以通过流通速度变化来计算。但是，从定性分析的角度来看，费雪方程式无法帮助我们找到正确的方法，查明流通速度变化的条件。然而，我应该补充一点，这种反对意见可能不太适用于美国银行业的统计数据。因为，美国的统计数据将定期存款和活期存款加以区分，这大致相当于储蓄存款和活期存款的区别；而透支在美国对减少现金持有量所起的作用可能较小。费雪教授的M只包括活期存款。

但无论如何，补救这一不足之处并不难，同时这样做也许是值得的，具体如下：

（1）令w=活期存款占存款总额的比例，

可得Mw=活期存款数额，

以及M（1-w）=储蓄存款数额。(www.daowen.com)

（2）令w′=可透支额度占活期存款的比例，

可得Mww′=可用透支额度，

以及Mw（1+w′）=现金总额。

（3）令V=活期存款的流通速度，即货币支付总额与活期存款总额之比，

以及V′=现金流通速度，

可得B = MVw = MV′w（1+w′），其中B是现金交易总额。

由此得出

P2T = B = MVw = MV′w（1+w′）

或者

和费雪的方程式一样，这一方程式只是进一步说明“现金总额×流通速度=银行票据交换总额”。

在没有透支款项和储蓄存款的情况下，即在w=1和w′=0的情况下，方程式（1）可简化为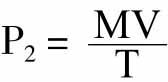，这与费雪的方程式相同。

在没有存款只有透支的情况下，即M=0，方程式（1）可化简为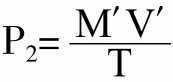，其中M′是可用透支额度。