上面讨论的“实际余额”方程式源于一种方法，对那些在剑桥大学的教室里听过马歇尔和庇古教授讲课的人来说，这种方法早已耳熟能详。因为这种方法近来很少在其他地方使用，所以我称之为“剑桥”数量方程式。但是这一方程的历史（参见第133页脚注〔1〕）更为久远，源自佩第、洛克、康梯龙（Richard Cantillon）和亚当·斯密。马歇尔对其实质总结得非常到位：

在每一种社会形态中，都有一部分收入值得以货币形式存在，可能是五分之一，或者十分之一，或者二十分之一。以货币形式支配大量资金，使买卖变得更顺利，同时使商人在议价中处于有利地位；但是如果将其用于添置家具，将会给人带来满足，或是用于购置机器或家畜，将带来货币收入。一个人在权衡了增加资金支配权的优势，与把更多的资金转化成一种无利可生的形式的劣势之后，便可以确定货币与固定资产的合适比例……假设一个国家的居民，考虑各种情况，包括各种各样的性格和职业，值得持有十分之一年收入的平均现成购买力，加上五十分之一的财产，那么该国货币的总价值将等于这些金额的总和。[45]

剑桥大学旧照

剑桥学派是19世纪末由英国著名经济学家马歇尔创建的一个有较大影响的学派。主要代表还有后来成为福利经济学派先驱者的庇古，以及后来成为新剑桥学派的主要代表人物的D. H．罗宾逊。由于他们先后均在剑桥大学任教，故被称为剑桥学派。

庇古教授将这一理论转化为一个数量方程式：[46]

在日常生活中，人们在偿还以法定货币订立的债务时，需要不断地进行支付。多数人也有一系列类似的对自身有利的债权。但是，任何时候到期的债务和债权，很少能够完全相互抵消，其差额必须通过转让法定货币的所有权来弥补。因此，每个人都急于以法定货币形式拥有足够的资金，既能使他顺利完成日常生活中的交易，又能保证满足不时之需。为了实现这两个目的，人们一般选择以法定货币的形式持有一定数量小麦的总价值。[47]因此，在任何给定时间都有一个明确的对法定货币所有权的需求清单。令社会拥有的以小麦表示的总资金[48]为R，以法定货币形式持有的这些资金的比例为k，法定货币的单位数量M，以小麦表示的每单位所有权的价值或价格为P。然后需求清单可以用方程式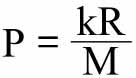表示。

庇古教授接着将这一方程式继续扩用，应用到部分现金以法定货币形式持有，部分现金以银行存款形式持有的情况中，即：(www.daowen.com)

其中c是公众以法定货币形式持有现金的比例，h是法定货币与银行家持有存款的比例。

显然，这一方程式形式上是正确的。问题是，这一方程式是否清楚地揭示了重要的变量。在我看来，这一方程式似乎还存在以下问题，其中一些问题同样存在于我在《货币改革论》中提出的数量方程式：

（1）引入社会日常收入R，表明日常收入变化是现金资源需求产生了直接影响，这是直接影响现金需求的两个或三个最重要的因素之一。就收入存款而言，我认为这是正确的。但是，在讨论存款总额而非单独讨论收入存款时，R的重要性就大大降低了。事实上，“剑桥”数量方程式的主要弊端在于，它把主要与收入存款有关的考虑因素应用到总存款中，在解决问题时，就好像某些决定收入存款的因素也能决定总存款。第10章末尾给出的公式，将收入存款分离出来，然后单独应用“剑桥”方程式，旨在保持“剑桥”法的本质优势。

（2）当该方程式应用于收入存款以外的情况时，将银行存款占社会收入的比例k放到首要位置，容易使人产生误解。该方法强调的重点是，所持有的实际余额取决于以现金和其他形式持有的资金的比较优势，所以k的变化可归因于这些比较优势的变化，这一点很有用也很有启发意义。但是在这里，“资金”不能像庇古教授那样理解为和本期收入一样。

（3）庇古教授用小麦来衡量实际余额的数量，是在回避而不是解决基本方程式所要导出的物价水平这种问题。任何数量方程式的目的，都是在某种意义上计算出货币购买力，而不是小麦的价格。但是庇古的方程式不是无法得出货币购买力，就是暗示相对价格不变，因此，所有单个价格及所有物价水平都是以小麦计价，这与事实相去甚远。

（4）这个方程完全掩盖了由存款比例变化产生的影响因素，实际上这是最重要的影响因素之一；存款因用途不同可分为储蓄存款、商业储蓄和收入储蓄。此外，由于储蓄和投资之间的差异，很难分析影响物价水平的因素。