如上所述，要比较两个点的货币购买力，正确方法是比较两个点上“同类人”的货币总收入。但这种比较方法在实际应用中存在困难，并没有客观的考查方法来确定进行比较的“同类人”。所以到目前为止，一般做法不是试图寻找一对“同类人”，然后比较他们的收入，而是找两份支出明细表，我们认为可代表不同点上同类人的消费情况，然后比较表中两种“等价”复合商品的价格。

但是，通过直接比较“同类人”的货币收入，或通过间接比较“等价”复合商品的价格，都不太可能完全准确。因此，我们面临一个问题：近似法。我认为，当前有些人使用近似法时，没有足够清楚地认识到比较对象是什么，因此所采用的方法并不准确。在接下来的讨论中，我将分析不同的近似法到底是怎么回事，又有什么条件；而在我看来，这些方法有的行得通，有的行不通。

A．直接比较同类人收入的方法

统计学家们完全摒弃了这种方法，但实际上这却是最常用的靠常识的方法。这种方法要求首先要熟悉这两个比较对象的生活条件，然后用常识来判断比较对象的生活水平，所以这种方法取决于常识判断。一个苏格兰人在伦敦获得了一个工作机会，或者一个英国人在澳大利亚或美国或是德国获得了一个工作机会，这时此人想知道与他此时此地的收入相比，在新地方即将获得的货币收入“价值”几何，也就是说，新地方的货币购买力相对是多少。此人通常不查阅任何官方指数，因为即使查阅了，也不会得到非常有用的答案。他会询问熟悉两地生活情况的朋友。这位朋友在他的脑海里想象出两个人，每个地方一个，在他看来这两人生活水平大致相同，然后比较他们的收入，最后根据这个比较做出回答。这位朋友可能会告诉他，爱丁堡500英镑的年薪，或者伦敦700英镑的年薪相当于纽约1200英镑的年薪。也就是说，在这个收入范围内，货币购买力的比例为12:7:5。但对于工人来说，不一定就是这个比例。

同样的方法可以用来比较不同时间的购买力，前提是要记得这段时间的生活水平。我们经常问，一个特定阶级的购买力与战前相比如何，并根据对相对生活水平的大体记忆，判断中产阶级或农业工人等人的购买力比率是多少。

如果是训练有素的调查人员，他为此目的进行明确调查，然后基于调查结果做出比较，最后再经价格和消费统计数据来核实比较结果，那么结果可能确实非常有价值。即使是由于记忆和大体印象不可避免地会模糊、不准确，在以下两种情况中，比较结果也可能比我们从指数中得到的答案更准确：一种是支出特征发生巨大变化；一种是很大一部分支出不符合标准，指数无法涵盖。

例如，要比较英国人和东方人的货币购买力，最好是通过大体印象比较同等生活水平的成本，而不是比较其他方面，因为这两种人其他方面的消费习惯有很大差异。一对中产阶级夫妻，战前与战后的购买力，也可以根据总体印象进行比较，因为其中租金、佣人、教育和旅行等大部分支出必然不会包含在指数之内。

正是在这种情况下，直接法和间接法产生的结果会有本质不同，但直接法更接近事实。但是，如果标准化支出在特征上没有多大变化，例如工薪阶层五年前的支出和现在的支出相比较，那么间接法可能会更准确。

英国街上的书店

20世纪早期的英国，城市的人们生活方式已经和现代没有多大区别。街上有汽车、大型商场、书店、咖啡馆，还有独具特色的餐厅。在不少年份里，大部分普通人的收入一直保持稳定并随着经济发展而增长。

如果要避免负效用，根据总体印象作比较时，通常会充分考虑常规开支，这种开支用处不大，却是当地风俗习惯所需；要判断这种比较法究竟是好是坏，就会引出一个难以捉摸的问题：购买力究竟是什么，我不打算在这一问题上多费笔墨。

B．间接比较等价复合商品价格的方法

这种方法很常用。在确定购买力指数的那份表格上，我们最多只能知道不同商品的价格以及其支出分配，我们很少或者根本不知道哪两种人是“同类人”，也不知道可以用什么来补充这些数字。

然而一般来说，我们确实知道，部分支出（或大部分）在性质上相同，满足同类消费者需求的能力也相同。用a表示两个地点代表平均支出的那部分复合商品，所以对两个地点来说都是一样的，而不同的部分用b1、b2表示。在一个地点购买的商品数量相对另一个地点较多的情况下，当然这两个地点相同部分的数量为a，不一样的部分分别为b1、b2。另一方面，消费虽看起来相似，但由于偏好和环境不同，消费的实际收益也不同，因此a不包含消费，而b1、b2包含消费。其次，b1的数量单位必须使第一个地点上一个单位b1的支出，与一个单位a的支出之比等于b1的总支出与a的总支出之比；b2同样如此。

此外，有时也可以更进一步，在可以相互替代的两种商品之间建立等价关系。比如，如果一磅茶叶和两磅咖啡用途相同、功效相似，可以相互替代，那么只要价格相等，对于比较地点的大多数消费者来说，买一磅茶还是两磅咖啡几乎无关紧要；但是，在第一个地点一磅茶比两磅咖啡便宜，而在第二个地点一磅茶比两磅咖啡贵，因此，适合第一个地点的复合商品包括茶，而适合第二个地点的复合商品包括咖啡；此时我们可以将一磅茶和两磅咖啡视为大致等价，这并不会产生任何其他问题。同样，如果不同地方，饮食不同，小麦、燕麦、黑麦、马铃薯可以彼此替代，那么可以建立的等价比可能相当令人满意。就采用等价替换法的范围而言[29]，实际上a的范围扩大了，而b1和b2的范围缩小了，其中a指的是两个地点一样的消费，严格来讲是具有可比性的消费部分。当一种消费项目可以被另一种消费项目替代时，我们就可以确定这些项目之间的等价比率；因此，下文中的a包含这些消费项目。

尽管如此，b1和b2中仍有一些无法用对等替代法建立平衡对应的复杂商品。然而，一般来说，b1和b2组成的一些复杂商品仍然无法使用等价替代法。同类人从法老的奴隶身上获得的满意度，与从第五大道的汽车上获得的满意度是无法比较的；同样，昂贵的燃料和便宜的冰带给拉普兰人的满意度，与便宜的燃料和昂贵的冰带给霍屯督人的满意度，这两者也是无法比较的。

因此，我们用a+b1和a+b2分别表示两个地点的平均消费。我们已经假设，a能给两个地点任何两个“同类人”带来相同的满意度，如果a代表全部消费，我们便可以通过只比较a的价格来比较两个地点的购买力。剩余消费b1、b2不能这样等同起来，或用这么简单的方法进行比较。我们不能假设b1和b2是等价，也就是假设这两个地点的普通消费者同类人，同时，我们也不知道对于同类消费者而言，第一个地点给定数量单位的a+b1与第二个地点多少单位的a+b2等价。因此，我们面临的问题是找到一种适用于这种情况的有效近似法。这一问题我们必须现在解决。我认为只有两种方法合理可行，第一种更普遍适用，第二种方法提供了两种极端情况，而正确的方法介于两者之间。在这两种极端情况下，我们可以假设这两个地点除了相对价格之外，其他都没有变化。

1. “最大公约数”法

假设a在第一个地点的价格是p1，在第二个地点的价格是p2。第一种近似法忽略了b1和b2，用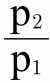表示这两个地点之间物价水平变化的指数。这种方法只要满足两个条件中的任意一个即可。假设两个地点任意两个同类人消费一单位的a所获得的满意度几乎相同。

第一个条件是，这两个地点的每一个消费者，在a上的支出都比在b1或b2上的支出要多。

第二个条件是，在第一个地点任何一个消费者，从a和b1的消费中获得的实际收入，与其在这些方面的支出大致相同；第二个地点的a和b2也是如此。

以上两种条件每一种的建立方式如下：令实际收入为E的人在第一个地点消费了n1个单位的a+b1，其中a的价格为p1，b1的价格为q1；在第二个地点的消费情况与此类似；第一个地点与第二个地点的货币购买力之比为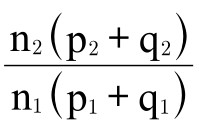。由此可得：

（1）如果q2、q1分别比p2、p1小，那么对于实际收入相等的人来说，n1与n2必须几乎相等，此时上述表达式的近似值为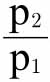。这与上述第一个条件相同。

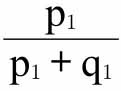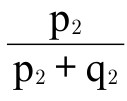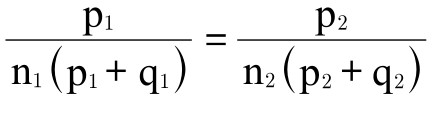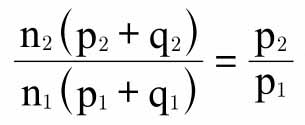（2）如果对于实际收入为E的人来说，在第一个地点从a和b1的消费中获得的实际收入与其在这些方面的支出大致相同，那么从n1a获得的满意度为E；在第二个地点同等条件下，从n2a获得的满意度为E。因此，如果在两个地点消费同样单位a获得的满意度大致相同，可得；因此为近似值。这与上述第二个条件相同。

若要比较多个购买力，只需满足上述条件中的一个，便能得到一个非常合理的近似值。只要第二个地点提供更多有用的支出商品，因这些新商品无法在第一个地点获得，第二个条件便不会成立。因为在这种情况下，从b2获得的单位平均满意度与从a获得的单位平均满意度的比例，要高于从b1获得的单位平均满意度与从a获得的单位平均满意度的比例，所以，如果要成功地比较购买力，除非满足第一个条件，否则还需要做进一步假设。因此第二个条件具有不确定性。

这种近似法将支出中的a部分作为比较基础，对所有比较地点而言，a是相同的；与分析同样的复合商品时一直采用的更复杂的公式相比，忽略其余部分支出优势更大，因此，这种近似法不需要用到联算法，往后将会讨论这一方法。实用统计学家一直把a+bl或a+b2应用于所有情况，而相比之下这种近似法明显更可取，同时也不复杂。一般来说，统计学方法所产生的误差比从头到尾使用a所产生的误差还要大。只要消费特征变化是由相对价格的变化导致的，就意味着消费者行为变化转而购买相对便宜的商品，因此与不太适合复合商品的地点相比，统计学方法往往高估完全适合复合商品的地点的购买力。

因此，在这些情况下，除了相对价格以外其他都没有变化，这种所谓的“最大公约数”法可能会得出其所能得到的最好结果。例如，把连续十年期间每年总支出的最大公约数作为折中复合商品，就可以得到这段时期内购买力的最佳指数。为了验证近似值的准确性，在这一指数旁边说明每年总开支所占比例，这对所有年份来说都是一样的。无论如何，与迄今尚未采用的从头到尾使用a的方法相比，从头到尾使用a+b1的方法在我看来没有什么可取之处，但不足之处却不少。

一般来说，随着共有支出所占比例越来越小，如果从头到尾还是用a做近似值，那么这个值将会变小。但是要想得出更好的结果，必须多加使用等价替代法，从而增加a涵盖的范围的比例，而不是使用一些诸如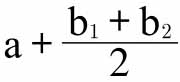此类的中间公式。然而，实际上，等价替代法除了应用于某些对不同地区工薪阶层生活水平的比较调查之外，迄今尚未应用于科学领域。在这些调查中，人们有时试图通过制定一种假定的等价体系，来解决工人饮食习惯变化的问题。[30]

在过去的一些调查中，即使a不再比b1和b2大，“最大公约数”法也许仍比任何其他可行方法都要好。比如，如果我们要粗略比较两个间隔很久的时间段，但时间相隔太久，等价替代法不太可行，那么我们唯一能做的只是选择两个时间点，对共有的少数几种重要的商品比较其价格。如果我们要为过去3000年的金币或银币价值编制一个消费指数，我想除了根据这一时期的小麦价格和劳动力日薪拟定复合商品之外，便没有更好的办法了。[31]角斗士与电影院之间不存在等价替代，买奴隶带来的便利与买汽车带来的便利之间也不存在等价替代。

农场工人

19世纪末20世纪初，得益于工业的发展，大农场也实现了机械化。农业摆脱了低效率的个体经营，成为了资本青睐的又一产业。

2. 极限法

现在我们可以假设，进行比较的两个地点中消费者偏好基本相同，同时除了相对价格之外其他都没有变化。在这种情况下，可以认为以商品计算的某一特定收入，能在这两个地点产生相同的实际收入。因此，虽然第二个地点的消费特征由于相对价格的变化而发生了变化，但是我们可以肯定，相应的实际收入与第一个地点类似的消费分配所产生的收入是相同的。

考虑到这些因素，便有办法可以确定出真正的比较必须存在的范围。

设P和Q分别为第一个地点和第二个地点代表支出的复合商品。

设第一个地点1英镑可以购买P的数量为P个单位，第二个地点1英镑可以购买Q的数量为Q个单位，p为每单位P在第二个地点的价格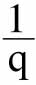，为每单位Q在第一个地点的价格。令实际收入为E的同类人在第一个地点购买n1个单位的P，在第二个地点购买n2个单位的Q。

那么，由于同类人在第一个地点的货币收入是n1英镑，在第二个地点的货币收入是n2英镑，所以比较这两地的购买力的指数为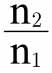。可以看出这一指数必须介于p和q之间。

由于第一个地点可以选择购买n1个单位的P，或者n1q个单位的Q，消费者倾向于购买前者，同时，由于购买前者获得的满意度和购买n2个单位的Q一样，可以推出n2＞n1q；同理，由于在第二个地点可以选择购买n2个单位的Q，假设购买n1个单位的P与此获得的满意度相同，或者购买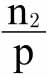个单位的P与此获得的满意度相同，同时消费者倾向于购买前者，可以得出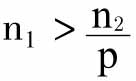；因此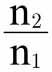，的值介于q和p之间，比q大，比p小。

因此，如果q比1大，货币价值必然下跌；如果p比1小，货币价值必然上涨。无论货币价值如何变化，总是介于p和q之间。

尽管上述公式比之前给出的公式更简单，证明也更严谨，但这个结论并不陌生。例如，庇古教授曾经在《福利经济学》第一部分第六章得出同样的结论。哈伯勒在《指数的意义》的第83至94页也很好地阐述了这一问题。然而，这一观点要基于消费者偏好相同这一假设，但这一点并没有得到充分的重视。[32]此外，必须注意的是，在p小于q的情况下，这个情况表明消费者偏好一定发生了变化，因此，假设消费者偏好不变不成立，因为这不符合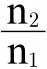小于p大于q这一条件。

在某些情况下，将最大公约数法和极限法相结合也许可行。我们也许知道，以支出来衡量，大部分人的消费偏好会保持不变，也清楚从这部分消费获得的实际收入，要么是实际总收入中相当大的一部分，要么是固定的一部分。在这种情况下，近似法首先应采用最大公约数法，将比较范围缩小到比较地点消费者偏好可假设为不变的那部分支出，然后在这一范围内使用极限法。

3. 公式交叉法

欧文·费雪教授对这种方法倾注了大量的精力[33]，并将其命名为“公式交叉法”[34]。实际上这种方法拓展了极限法，但在我看来，这种拓展不合理。

这一方法采用的推理具有如下特点：如前，假设P为适合第一个时间、地点或阶级的复合商品，一个单位的P在第一个点花费1英镑，在第二个点的花费为p；设Q为适合第二个点的复合商品，一个单位的Q在第二个点的花费是1英镑，在第一个点的花费为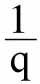。然后，如上所述，假设偏好等因素不变，而且只有相对价格变化，那么关于这两个点物价水平真正的比较尺度必然介于在p和q之间。费雪教授（和其他人）由此得出结论，p和q之间肯定存在某种数学函数关系，可以准确估算这个介于p和q之间的真实值。从这几方面出发，他提出并研究了许多公式，目的是尽可能找到真正的中间值的近似值。

现在，在我看来，比较之下的物价水平之间的比例，一般不存在任何确定的关于这两个表达式的代数函数。我们可以在p和q之间构建各种代数函数来确定这个点的值，但二者之间并无函数关系。此时我们面临着一个概率问题，在任何特殊情况下，我们都可能有相关数据，但如果没有这些数据，概率根本无法确定。

庇古

庇古（1877—1959年）是英国著名经济学家，剑桥学派的主要代表之一。《福利经济学》是庇古最著名的代表作，该书是西方资产阶级经济学中影响较大的著作，它将资产阶级福利经济学系统化，标志着其完整理论体系的建立。

出于这个原因，我认为费雪教授的长篇讨论中，并没有任何实质内容。在研究了大量公式后，他得出了这样的结论，即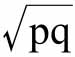（在我看来）理论上是理想的，也就是从数学计算上来说，这个公式可能比其他公式更接近真实值。这个结论来自于许多检测的结果，例如，该公式必须同时检测两个极端两边的值。然而，所有这些检测并不是为了证明这公式本身是正确的，而是与另一种先验公式相比，它受到的反对意见更少。这些检测也没有证明其中任意一个能计算出近似值的公式是成立的。

然而，如果我们不把介于p和q的之间公式当作可能的近似值，而只是为了方便说明所使用的表达式，那么考虑到代数优美、计算简单省力，同时在不同情况下使用一种特殊缩写表达式具有内在一致性，我们可能会受到影响，这是合情合理的。如果p和q出入很大，任何形式的缩写表达式都可能产生严重的误导作用，但如果p和q几乎相等，那么使用“介于p和q之间”这种表达可能会很麻烦，而选取某个中间数字会更方便，也不会引起误会，就算这个数字的选择相当随意也是如此。因此，如果了解到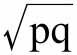等公式只不过是“p和q之间”的缩写表达式，我就不反对它们。

因此，事实上费雪教授的公式通常不会有什么问题，对这个公式持反对意见的理由是，当没有其他合理比较时，使用这个公式可以很容易地得出比较。该公式无法让计算者明白计算过程中出现的错误的性质和程度，而不是像之前的公式那样。费雪教授的公式之所以受到谴责是因为，无论消费者偏好还是其他因素是否发生变化，这个公式表面上似乎可以同样便利地对任何两种物价水平的数值进行比较。以常识判断明显不可能进行比较时，这种公式可以得出一个结果；而当完全适用的复合商品十分接近，相互之间的任何折中数也会得出一个合理的近似值，这两个结果一样好。

这类公式中最老的一个，是许多年以前由马歇尔与埃奇沃思两人独立地提出的（参看埃奇沃思《政治经济学论文集》第一卷第213页）。尽管费雪教授称之为“权重交叉法”，而不是“公式交叉法”，也仍然属于这一类，并且也同样是有异议的。这种近似法比较这两个地点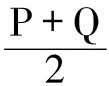的价格，也就是假定两种完全适用于这两个地点的复合商品，它们之间的第三个复合中间值大致适用于这两个地点。根据上述表示符号，这相当于用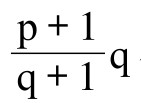衡量物价水平变化。[35]

马歇尔

阿尔弗雷德·马歇尔（1842—1924年），英国经济学家，新古典学派的创始人，19世纪末和20世纪初英国经济学界最重要的人物。在马歇尔的努力下，经济学发展成为一门独立的学科。剑桥大学在他的影响下建立了世界上第一个经济学系。

在我们结束这个讨论之前，通过一个例子来说明，当偏好和环境发生变化时，即使p=q，p和q也不能合理地衡量货币价值的变化。

假设在第一个地点牛肉和威士忌（各1个单位）是主要的支出对象，在第二个地点大米和咖啡（各1个单位）是主要的支出对象，又假设第二个地点牛肉和咖啡的价格比第一个地点便宜50%，而第一个地点威士忌和大米的价格比第二个地点便宜50%，则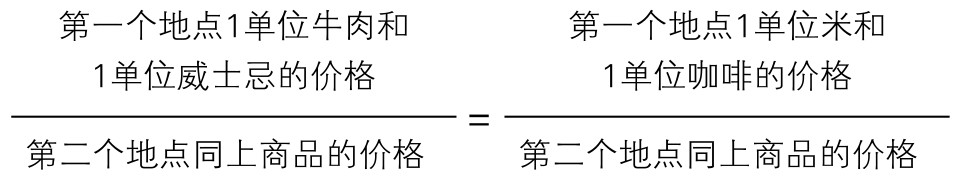（单位选择是这样的：第一个地点牛肉和威士忌的支出是相等的，第二个地点大米和咖啡的支出是相等的）。假设第一个地点根本不消费咖啡和大米，第二个地点也不消费牛肉和威士忌，这种假设只是为了表示简单方便，对于我们的讨论来说并不重要。如果将第一个地点咖啡和米饭的权重相对减少，将第二个地点牛肉和威士忌的权重相对减少，基本相同的方程式仍将成立。如果忽略极限法所需的条件，假设费雪教授的理想公式的基本观点普遍有效，我们可以从上面得出一个完全确切的结论：第一个地点主要消费牛肉和威士忌，第二个地点主要消费大米和咖啡，而这两个地点的购买力是完全相同的。然而，这个结论可能大错特错。例如，假设在第二个地点，尽管大米比第一个地点要贵一些，但因为气候原因，大米比牛肉更受消费者青睐；而同时仅仅因为咖啡更便宜，咖啡比威士忌更受消费者青睐，所以如果威士忌和咖啡一样便宜，威士忌便会受到消费者的青睐。如果我们了解这两个地点的“同类人”的货币收入情况，也许会发现第二个地点的货币购买力比第一个地点的要低很多。

4. 联算法

马歇尔首次引入“联算法”来编制一系列指数，该方法假设要比较的一系列点中任意两个连续点之间的差异很小，然后论述消费特征的变化问题。他还假设连续的小错误是不会累积的，虽然我们一般不这么说。然后他进行了一系列比较，第一个比较假设适用于第一个位置地点的复合商品，实际上与适用于第二个地点的复合商品等价，第二个比较假设适用于第二个地点的复合商品，实际上与适用于第三个地点的复合商品等价。

该方法如下所示：(www.daowen.com)

令p1、p2为适用于第一个地点的复合商品分别在第一个地点和第二个地点的价格；

令q2、q3为适用于第二个地点的复合商品分别在第二个地点和第三个地点的价格；

令r3、r4为适用于第三个地点的复合商品分别在第三个地点和第四个地点的价格；以此类推。

令n1、n2、n3为比较连续几个地点物价水平的一系列指数。

然后根据联算法用n1计算出n2、n3：

以此类推。

因此，通过两种方式将每个地点与其相邻地点进行比较，然后假设这两个不同的测量值近似相等，最后得出最终结果。换句话说：

如果n1是完全适用于第一个地点的物价水平；

如果n2是完全适用于第二个地点的物价水平；

如果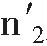是通过假设适用于第一个地点的复合商品，也适用于第二个地点时在第二个地点取得的物价水平；

如果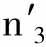是通过假设适用于第二个地点的复合商品也适用于第三个地点时在第三个地点取得的物价水平；

则

所以，假设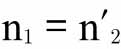，可得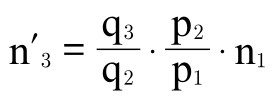；以此类推。

现在我们结合前面的论述，来分析上述计算过程是否正确。首先，上述论述假设消费者偏好等不变；另一方面，不仅相对价格会变化，而且在后面几个地方增加了新的支出对象，而前面几个地方的消费者无法购买；同时假设一个地点的市场上的任何支出对象，仍在另一个地方的市场上出售并没有撤出。其次是假设n2约等于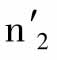，只有在我们用极限法来比较这两种情况，并且得出p约等于q这一结论后，这一点才算合理（数学符号以本书第64页的设定为准）。第三，假设连续近似值的小误差并不是累积起来的，因此，当这个计算过程在连续地点上重复若干次时，不会累积成一个很大的误差，这个假设最重要。

如果每两个连续地点彼此非常相似，那么第二个假设则可能成立。但是，尤其是在通常建议使用联算法的情况下，即比较时序数列，第三种假设更为危险。例如，假设近似等价的每一种替代品逐渐略微有所变化，也就是如果就这一目的而言，新的复合商品比上一个复合商品略微好一点，而且不太可能比前一个稍微差一点，此时联算法将产生累积误差。由于这个原因，如果将联算法应用于一段时间内，同时在这段时间内随着机会的不断增加，习惯也在逐渐改变，那么这可能误导我们。因为在这种情况下，与前一个日期相比，联算法低估了后一个日期内的货币购买力。实际上，联算法假设人造黄油第一次进入市场时其优势微不足道，已消费的人造黄油实际上与被其取代的天然黄油（或其他消费品）具有相同的优点；消费每次逐渐转移到新的，或改进的，或相对便宜的商品上时都是如此。

另一个强烈反对联算法的观点是，两个地点之间的比较，取决于这期间价格和消费特征会如何变化。例如，可能一开始价格和消费是这样的，然后中间发生了严重干扰（如战争），从而使相对价格和消费特征发生重大变化，但经过一段时间恢复均衡之后，价格和消费会恢复到原来的水平。显然，这种情况下之前的货币购买力和之后的货币购买力完全相同。但是如果运用联算法，没法保证指数会恢复到原来的水平，事实上它确实不会恢复到原来的水平。[36]

最后，联算法统计起来比较烦琐，不便应用于实际当中，所以尽管距离问世并得到认同已经过去了很多年，人们还是很少使用联算法。虽然接受联算法的都是理论家，但我认为这并不值得更多人的认可。

因此，我的结论是，不妨拿今天和五十年前的货币购买力作比较，比较性质基本不变的那部分开支的价格，我不知道实际比例是多少，比如说50%到70%吧；然后补充列出减少和增加的支出项目，以便对情况改善的程度做出大体判断；不要在中间这段时间逐年采用联算法来比较物价水平。

因此，除了直接估计同类人的收入水平之外，最大公约数法辅以等价替代法和极限法才是唯一有效的近似法。

尽管在实践和理论上有许多困难，实际中仍可以经常对购买力进行有效比较，这是因为：即使是当单个商品的相对价格和绝对价格都波动时，一般来说，在时间和空间相差不远的两个社会之间，常规支出和普遍偏好的一般特征，以及实际收入的平均水平并不会迅速或大范围发生变化。因此，由于消费结构变化以及偏好环境变化而产生的问题并不严重。例如，根据鲍利博士的观点，有证据表明1904年至1927年间，英国工薪阶层消费的一般统计数据显示，英国人在偏好和习惯上的变化相对较小。

[1]见马歇尔（Alfred Marshall）的《货币、信用与商业》（Money、Credit and Conmerce）第21页。“货币的一般购买力”通常指货币在一个国家（或者一个地区）以其实际消费比例购买商品的能力。同样见该书第30页：“货币的一般购买力应该以最终消费者购买成品时的零售价格来衡量。”

[2]相关重要文献比较少，有：1. 杰文斯（W.S.Jevons）转载于《货币金融研究》（Investigation in Currency and Fiance）一书中的论文。
　　2. 埃奇沃思转载于《政治经济学论文集》（Papers Relating to Political Econmy）第一卷中的论文。
　　3. C.M. 沃尔什（C.M.Walsh）：《一般交换价值的衡量》（The Measurement of Central Exchange-Value）。
　　4. 欧文·费雪：《货币购买力》（The Purchasing Power of Money）和《物价指数的形成》。
　　5. 韦斯利·米切尔：《批发物价指数》（Index-Numbers of Wholesale Prices，美国劳工统计局公报173页及284页）。
　　6. 阿瑟·塞西尔·庇古（A.C.Pigou）：《福利经济学》（The Economic of Welfare）第一部分第五章。
　　7. 戈特弗里德·哈伯勒（G.Haberler）：《指数的意义》（Der sinn der Indexzahlen，1927年）。
　　8. M. 奥利维尔（M.Olivier）：《物价指数变动》（Les Nombres Indices de la Variation des Prix，1927年，对现有文献的总结与评价）。
　　费雪教授正在编写一本现有物价指数的词典。

[3]在美国现称生产者价格指数（Producer Price Index）。它是反映不同时期商品批发物价水平的变化程度和趋势的指数。西方各国编制的批发物价总指数并不是包括全部的商品，而是只包括比较重要的有代表性的那些商品。

[4]关于他的方法，请参阅其《商业周期与商业测量》（Business Cycles and Business Measurement）第六章，以及《纽约联邦储备银行月刊》（The Federal Reserve Bank of New York）。

[5]后来，斯奈德于1928年2月在《经济统计评论》出版了修正后的1913至1927年“物价总水平指数”，其编制思路与上述略有不同。但是，与上面给出的版本相比，这个新指数作为消费指数却没那么实用。斯奈德的目标是编制一个现金交易指数，而不是消费指数，为了实现这一目标，新指数不仅要将消费品和劳务计入在内，而且还要考虑房地产价值和证券价格。因此，尽管斯奈德的新指数可能更适合他的目的，但他的旧指数肯定更适合我的目的。

[6]指以魁奈（Francois Quesnay，1694—1774年）为代表的重农学派，因在当时法国学术界影响很大，故直接称他们为经济学家。魁奈是法国重农学派的创始人和主要代表，古典政治经济学的奠基人之一，代表作品是《经济表》（Tableau Économique）。

[7]我认为马歇尔对使用批发价格标准代替不存在的消费价格标准作出的解释是，省略的服务往往与省略的加工品相互抵消。但是，如果认为这两种误差刚好可以抵消，那就大错特错了。

[8]埃奇沃思在他的英国协会备忘录中，将这些指数描述为“所有模式和方法之间的折中——如果在紧急情况下，我们只能采用一种方法，而非多种方法……那么综合考虑各种不同的因素，我们推荐这种方法，就像在詹姆斯二世（James Ⅱ）去世后宣布王位空缺这一著名决议一样”。（见本书161—162页）

[9]参见我对沃伦（G. F.Warren）和皮尔森（F. A. Pearson）《供给与价格的相互关系》（Inter-relationships of Supply and Prices）一文的评论，本文发表在《经济学杂志》（第十一期第92页）上。

[10]例如，在这一时期一种商品的价格在英国上升了10%，在美国上涨了20%，美国一栏中的上述指数便是109，也就是（120/110）×100。

[11]关于英国对这一指数的讨论，参见《经济学杂志》第十三卷第628页鲍利的文章，《经济学杂志》第二十二卷第630页及第三十三卷第476页我的文章，《经济学》（1924年2月）第1页贝弗里奇（William Beveridge）的文章，《经济学杂志》第三十四卷第286页罗伯逊的文章，《经济学杂志》第三十五卷第1页陶西格（F. W. Taussig）的文章。

[12]我在《货币改革论》中列举了一些例子。

[13]鲍利教授在《价格变动国际对比》（International Comparison of Price Changes）与《十一个主要国家的物价指数对比》（Comparative Price Index-Numbers for Eleven Principal Countries）中讨论了采用本地批发物价指数时不同的加权体系所引起的误差量（《伦敦和剑桥经济研究所》特别备忘录1926年7月第19号和1927年7月第24号）。

[14]关于这一理论更详细的讨论，参见我的《货币改革论》（第87页），也可参见卡塞尔的《1914年以后的货币和外汇》（Money and Foreign Exchange after 1914）以及凯劳（Wilhelm Keilhau）博士在《经济学杂志》（1925年第35期第221页）上发表的文章。

[15]关于这一理论更详细的讨论，参见我的《货币改革论》（第87页），也可参见卡塞尔的《1914年以后的货币和外汇》以及凯劳博士在《经济学杂志》（1925年第35期第221页）上发表的文章。

[16]不同于他所说的“货币力”，或现代术语中所谓的“货币购买力”。

[17]沃尔什和埃奇沃思在《经济学杂志》等刊物上，就从概率计算中得出的某些观点是否适用于物价指数展开了长期的争论。在这场争论中，我大体上支持沃尔什。阿林·杨（Allyn Young）教授以前略微偏向于支持“有瑕疵”的英国学派，后来1923年转向支持另一派（参见他的《经济问题》，第294至296页）。在欧洲大陆，意大利教授基尼（Corrado Gini）以及奥地利哈伯勒博士则没有受英国“瑕疵观点”的影响，不过法国的吕西安·马尔西（Lucien March）受到了影响，但是迪维西亚（Francis Divisa）显然没有受影响。从马歇尔的某些观点可以看出他没有受到影响，但是他从没明确讨论过这一问题。

[18]最初我是在一篇关于物价指数的论文中尝试讨论这一点，虽然不够充分，但这篇论文在1907年获得了剑桥大学的亚当·斯密奖金。

[19]埃奇沃思在1887年为英国协会编制了一份备忘录，这一目的与备忘录第八节和第十一节中的“不确定标准”相同，转载于他的《政治经济学论文集》第1卷第233页及后面部分。他在第八节中试图“不考虑商品数量确定指数：前提是假设有许多商品的价格随着市场的完善而变化，从而影响货币的供给”。第九节试图“利用商品数量确定指数：前提是假设价格的一般变动是由同一个原因导致的”。

[20]同样参见鲍利博士《指数简介》（Notes on Index Numbers）的第一部分。（《经济学杂志》1828年6月）

[21]一些作者通过观察实际出现的单个价格的分布情况来解决这个问题，看它们是沿着算术平均值对应的高斯曲线分布还是沿着几何平均值对应的曲线分布……关于这种方法所得结果的详细说明，请参见奥利维尔的《论指数》（Les Nombres Indices）第四章，另见鲍利的《指数简介》（《经济学杂志》1928年6月第217至220页）。但在我看来，这种方法似乎考虑不周，除非是为了达到消极的目的，也就是说除非将其应用于大量数据，否则价格分布毫无规律可言。把这种方法应用于少量数据，就像物价指数所做的那样，除了证实我们预计从事实推断出的结果之外，什么也证明不了。如果结果表明多种不同情况下价格分布曲线是相同的，那么这将引起关注；但就目前所做的研究而言，却还没有发现这种问题。然而，值得一提的是，奥利维尔和鲍利教授都得出结论，就曲线拟合而言，在他们研究的情况中几何曲线比算术曲线拟合得更好。

[22]迪维西亚是为数不多敢于指出这一点的作者［参见《货币指数》（L'I ndice monétaire et la théoire de la monaire），原载于《经济政策评论》（Revue d'É conomic Politique）1925年第858页］，同样参见奥利维尔《论指数》第106、107页。迪维西亚表明，不仅相对价格变化的相关性证明高斯误差定律不适用于此，而且一个所谓的“货币”原因，无论如何定义，都会平等地影响所有价格——这个假设没有根据。

[23]关于这一点，我已经在《货币改革论》（第四卷）第一章“货币价值变化对社会的影响”中阐述得非常详细，在此无须重复，原文如下：“货币单位的变化因方式相同，对所有交易产生同等影响，所以相当于没有影响。此类变化过去和现在都造成了巨大的社会影响，因为，众所周知，货币价值变化对不同的人、不同目的产生的影响是不一样的。”同样参见我的《丘吉尔政策的经济后果》（Economic Consequences of Mr. Churchill，．第九卷第三部分）。

[24]这一章论述了一个特殊的技术难题。急于解决货币问题的读者可以略过本章。

[25]接下来为了避免不必要的麻烦，我假设敏感程度相同。

[26]哈伯勒在他的《指数的意义》第81页中充分阐述了货币收入、商品收入和实际收入三者之间的区别对物价指数理论的重要性。

[27]实际上，在第一种情况下取的是2、3、4的算术平均值，而在第二种情况下取的是调和平均数的倒数。

[28]这一问题和我在《概率论》第三章，尤其是第七至十六节（第八卷）中讨论的问题相同。

[29]我认为埃奇沃思可能也想到了这种方法，这一点在下面这段难以理解的文章（《经济学杂志》第35卷第380页）中有所体现。我们确实可以用商品建造一艘“船”，其中商品数量质量确定，随时间而变化的价值可构成一系列指数。但就是在开始建这艘船的时候，我们的商品数量便不再绝对客观。因为在选择商品种类时，必须考虑到实用性。无论如何，出海时船的构成发生巨大的变化，我们必须放弃陆地上那种比较价格的方法，改变那种比较满意度的更不确定的方法。因此，如果一段时间内商品价格和数量发生巨大变化，那么鲍里教授将会比较这点——价格固定时从不同商品组合获得的“满意度”。

[30]根据埃奇沃思的说法（《政治经济学论文集》，第213页），德罗比什（C. Drobisch）是第一个提出等价替代公式的人，不过该公式所依据的标准却不够好，实际上甚至有点荒谬。

[31]参见马歇尔《货币、信贷和商业》第21、22页：“记录主要粮食价格具有双重意义。因为除了我们自己所处的时代以外，目前为止每个时代的普通劳动者，大部分工资都用来购买这些粮食；以往实际耕作者都自己保留这些粮食，现在大部分粮食就是他们的工资。此外，长期以来粮食种植方法几乎保持不变。因此，在研究对象（国家或地区），普通劳动力的工资和标准粮食的价格代表一般价值。这种方法对如今任何一个西方国家来说都是不合理的。但在亚当·斯密和李嘉图时代，这是合理的；而对‘古典’学说的解读，也有必要借鉴其价值”。洛克（John Locke）早在两百年前就写道：“粮食是任何国家不变的普通食物，最合适衡量商品在任何长期内的价值变化。”参见《洛克全集》（Works）第五卷第47页。这种衡量货币价值的传统方法便运用最大公约数法，参见亚当·斯密的《国富论》第一卷第十一章。

[32]鲍利博士可能在1928年6月发表于《经济学杂志》上的《指数简介》中明确指出了这一必要条件。

[33]参见他的作品《物价指数的形成》。

[34]同上，第七章。

[35]鲍利博士在《指数简介》（《经济学杂志》1928年6月）中给出了他的公式优于其他公式的原因，前提是忽略连续性以及所有足够小的数量。

[36]伯森斯（Warren M. Persons）教授发表了一篇与上述内容相关的有趣分析，不过主要是研究联算指数与相应的固定基数指数发生偏差的情况［《经济统计评论》（1928年5月）《权重与关联度之间的相关性在指数构建中的作用》（The Effect of Correlation between Weights and Relatives in the Construction of Index Numbers），第100至105页］。