（一）确定企业文化评价的因素集

企业文化评价的因素集可设定为U＝（u1，u2，…，un），其中ui为影响评价对象的因素，i＝1，2，…，n。这里，可定义U＝{u1，u2，u3，u4}，U1＝{u11，u12，u13}，U2＝{u21，u22，u23}，U3＝{u31，u32，u33}，U4＝{u41，u42，u43}。

（二）确定企业文化风险评价的评语集

设评语集为V＝（v1，v2，…，vm），其中vj表示评价结果，j＝1，2，…，m，评价等级个数m通常为4～9。这里取m＝5，V＝（v1，v2，v3，v4，v5），即V＝（非常好，较好，一般，较差，非常差）。

（三）确定各评价因素间的权数分配

设A＝（a1，a2，…，an）是U的一个模糊子集，称为权重分配集；其中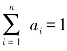，，a＞0，ai表示第i个因素在综合评价中的重要程度。

权重的确定采用Delphi法（专家调查法）、AHP法（层次分析法）等方法，为适合于模糊运算，一般要求权重的分量和为1。权重是表示各指标在目标评价中所起作用程度不同的系数，权重的确定对总体评价结果有重要影响。同一组指标值，不同的权重系数，会导致相差很大的评价结果。采用AHP方法确定指标体系权重，其步骤如下：

第一，建立递阶层次结构，将评价目标层次化。

第二，构造两两比较判断矩阵。为了比较某一层中指标对上一层某一个指标影响的相对重要性，邀请专家对同一层中的各指标进行两两比较，比较的结果即构成判断矩阵，这一步是进行层次分析法的关键。在进行两两成对比较时，为将相对重要性数量化，采用1～9标度，其含义见表7-3。

表7-3　1～9标度的含义

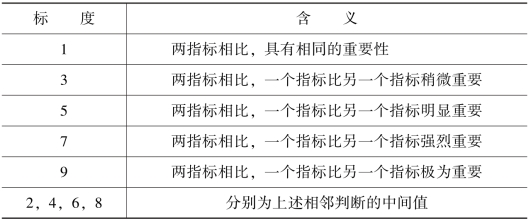
这样，对于同一层次n个评价指标，可得到两两比较判断矩阵A：

A＝aij()n×m

矩阵A具有如下性质：aij＞0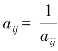；；aii＝1

第三，计算各评价指标的相对权重向量。对判断矩阵A，计算满足AW＝λmaxW的特征根和特征向量，以上公式中λmax为判断矩阵的最大特征根，W＝（W1，W2，…，Wn）为对应于λmax的正规化特征向量，W的分量Wi即是相应指标对上一层某一指标的权值。(www.daowen.com)

第四，两两比较矩阵的一致性检验。在对多因素进行比较的时候，人们往往难以保持比较前后的一致性。要使这种不一致程度保持在一个容许的范围内，就需要对成对比较矩阵进行一致性检验，其步骤如下：计算一致指标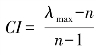，其中n为判断矩阵的阶数，λmax为判断矩阵的最大特征根；计算一致性指标CR＝CI/RI，其中RI为随机一致性指标，其数值大小见表7-4。当CR＜0.10时，就认为成对比较矩阵的不一致性在容许范围内，即该成对比较矩阵具有“满意的一致性”；当CR≥0.10时，则需对成对比较矩阵进行修正。

表7-4　随机一致性指标RI的数值

（四）确定模糊评价变换矩阵R

通过对每一个因素的判断，给出每个因素的评语等级，这样就建立起评价因素与评语等级之间的关系，即从U到V的模糊关系，这可用模糊评价变换矩阵R进行描述。

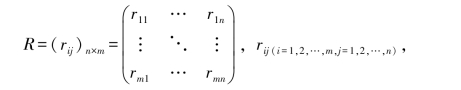
其中rij表示因素ui对评语等级vj的隶属度，0≤rij≤1。

（五）建立一级多因素模糊综合评价模型

鉴于单因素模糊评价只能反映一个因素对评价对象的影响。为了取得所有因素对评价对象的综合影响结果，需要进行综合评价。由因素集U上的模糊集A＝（a1，a2，…，an）和模糊评价变换矩阵R可构造出如下单级模糊综合评价模型：

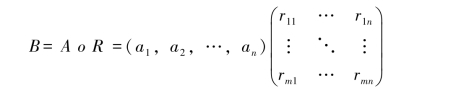
（六）多级模糊综合评价模型

在复杂系统中，由于要考虑的因素很多，多因素间往往还有多层次之分。对于这类多层次问题，可以先对诸子问题分别进行综合评价，然后再对总体进行综合评价，即先对低层次因素进行综合，再对高一层的因素进行综合，直至最顶层。多级模糊综合评价模型如下：

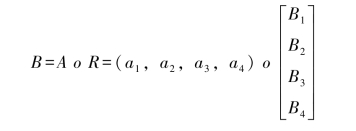
由以上公式可知：A为模糊综合评价中n个因素ui的权数（n＝4），即ui层对上一层的权重；Ai为ui{ui1，ui2，…，uik}中第个因素uij的权数分配，即uij层对ui层的权重分配；R和Ri分别为第一层和第二层的模糊评价变换矩阵。B为U的综合评价结果，这里采用德尔斐法和层次分析法（AHP）来确定A和Ai的权重值。