由于高新区创新网络环境支撑的Sig值为0．090，大于0．05，因此考虑删去此变量，就我国高新区创新网络的网络主体、网络联系对区域创新能力的影响进行回归分析。回归方程如式（6．15）所示：

其中，y代表各地区创新能力，x 1代表各地区高新区创新网络主体知识创新，x 2代表各地区高新区创新网络联系，α、β1、β2为待估参数，μ为随机误差项。

类似地，由附表B2可以看到，各解释变量间不存在多重共线性问题。

表6．14 高新区创新网络与区域创新能力多元回归结果

注：①*表示在10%水平上显著，**表示在5%水平上显著，***表示在1%水平上显著。
②括号内为t值。

由表6．14可以看到，该模型的相关系数R＝0.903，判定系数R 2＝0.815，调整的判定系数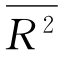＝0.806，回归估计的标准误差S＝0.343 051 07，拟合效果较好。(www.daowen.com)

由于F＝83.971，相伴概率值为0．000小于0．05，说明自变量与因变量之间存在显著的线性回归关系。

表6．14给出了线性回归模型的参数估计，其中高新区创新网络主体知识创新和高新区创新网络联系的显著性值均为0．000，小于0．05，因此其系数显著区别于0。回归方程如式（6．16）所示：

由于常量的显著性值远远大于0．05，故常数项非常不显著，可以忽略不计（见附表B2）。故标准化后的回归方程为：

综上所述，我国的区域创新能力不仅与高新区创新网络整体发展水平显著相关，而且与高新区创新网络的网络主体、网络联系有着显著的相关关系，随着我国高新区创新网络的网络主体、网络联系发展水平的提高，其所处区域的区域创新能力也显著提高。我国高新区创新网络环境支撑虽然也影响着其所处区域的创新能力，但其影响的显著性不如高新区创新网络的网络主体和网络联系。