（一）离散型异常数据清洗算法

对于ERP系统中生产管理模块的离散型异常数据，一般而言只能通过字段之间的关系来判断离散型异常数据的正确与否。常见的方法就是分类，这也是一种重要的数据检测和清洗方法，可描述如下：输入数据，或称训练集，由一条条的数据库记录组成，每一条记录包含若干个属性，组成一个特征向量。训练集的每条记录都有一个特定的类标签与之对应。该类标签是系统的输入，通常是以往的一些经验数据。

常见的分类方法有决策树归纳分类、贝叶斯分类、基于规则的分类以及还有一些其他分类算法如神经网络、遗传算法、粗糙集、模糊集方法等。在本章中我们将重点介绍决策树方法和神经网络的分类方法。因为决策树是一种比较直观简单的分类方法，也是一种常用的方法；BP神经网络分类是一种常见的基于模型的分类方法，该方法不仅适用于离散型数据，也适用于连续型数据。

1.决策树方法

决策树归纳是从类标记的训练元组学习决策树。决策树是一种类似于流程图的树结构，其中，每个内部节点表示在一个属性上的测试，每个分支表示一个测试输出，每个树叶节点存放一个类标号。树的最顶层节点是根节点。决策树算法的基本流程如图5-4-5所示。

图5-4-5　决策树算法流程图

属性选择度量是一种选择分裂准则，将给定的类标记的训练元组的数据划分D“最好”地分成个体类的启发式方法。常见的度量指标有信息增益、Gini指标等，由于Gini指标只适用于二叉树类型的分类，适用范围比较狭窄，我们将重点介绍信息增益方法。

信息增益属性选择度量是基于Claude Shannon在研究消息的值或“信息内容”的信息论方面的先驱工作。设节点N代表或存放划分D的元组。选择具有最高信息增益的属性作为节点N的分裂属性，该属性使结果划分中的元组分类所需的信息量最小，并反映这些划分中的最小随机性或“不纯性”。

对D中的元组分类所需的期望信息由式（5-4-11）给出

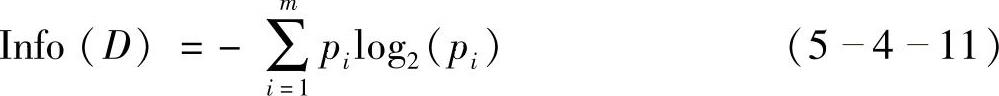
式中，p_i是D中任意元组属于类C_i的概率。使用以2为底的对数函数，因为信息用二进制编码。Info（D）是识别D中元组的类标号所需要的平均信息量，又称D为熵（Entropy）。

假设要按属性A来划分D中的元组，属性A根据训练数据的观测具有v个不同的值{a₁，a₂，…，a_v}。如果A是离散值则这些值对应于A上测试的v个输出。可以用属性A将D划分为v个子集{D₁，D₂，…，D_v}，其中D_j包含D中的元组，它们在A上具有值a_j，这些划分将对应于从节点N生长出来的分枝。为了实现准确的分类，我们需要计算属性A上的度量：

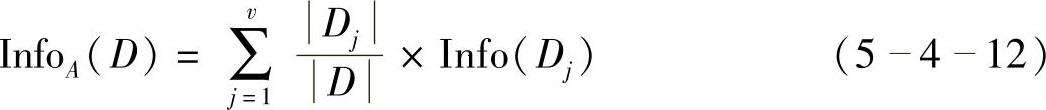
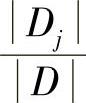充当第j个划分的权重，Info_A（D）是基于按A划分对D的元组分类所需要的期望信息，还需要的期望信息越小，划分的纯度越高。

信息增益定义为原来的信息需求与新的需求之间的类，即是

Gain（A）=Info（D）-Info_A（D） （5-4-13）

选择具有最高信息增益的属性作为节点N的分裂属性，这等价于按“最佳分类”的属性A划分，使得完成元组分类还需要的信息最小（即最小化Info_A（D））。

2.BP神经网络分类算法

前文提到BP神经网络用于预测，实际上BP神经网络不仅能够处理连续型数值，也可以用来处理离散型数值，当对BP神经网络设置多个输出节点时，就可以对数据进行分类。

（二）生产管理模块中的应用

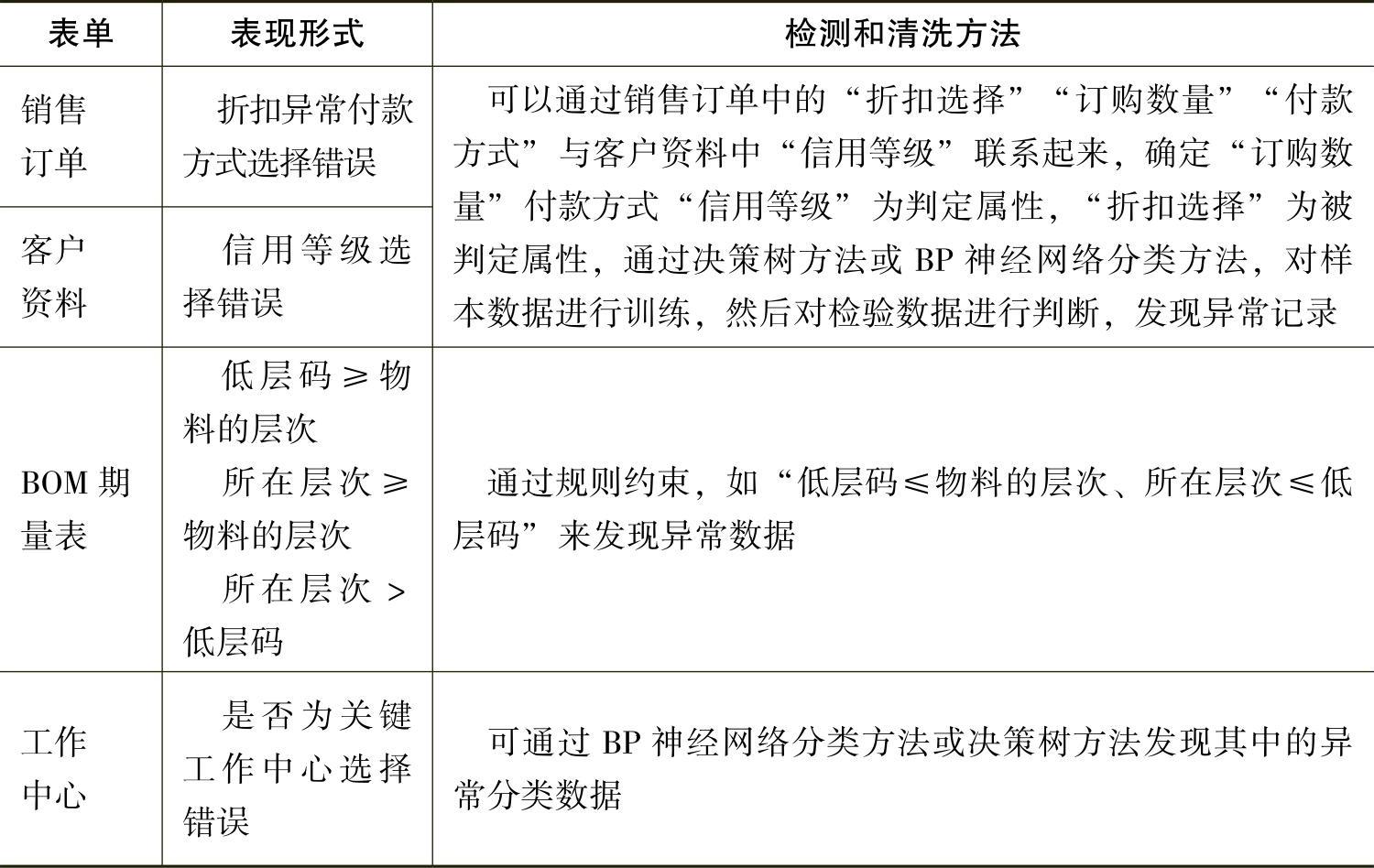
在生产管理系统中，离散型数值异常数据的表现形式如表5512所示，同时该表也指出了相应的检测和清洗流程。通常来说，离散型数值异常数据的检测是不能通过单个表单或单个记录来实现，必须结合其他记录以及其他表单中的属性，发现其中的规则，对违反规则约束的属性进行检测。一般包括以下几个步骤：①发现各离散型属性之间或与其他数据之间的关系，发现其中的判定属性和被判定属性，并通过决策树方法或者BP神经网络分类方法发现其中的异常记录。②通过一些约束规则来发现错误的记录，如BOM期量表中的“所在层次”必须小于等于“低层码”。

相对来说，离散型数值异常数据的清洗更加复杂，涉及的信息量更大。对于发现的异常数据，可通过以下方法进行清洗：①查找相关原始资料修改数据。②利用决策树、BP神经网络分类方法对异常数据进行修改。

表5-4-12　离散型数值异常数据的检测和清洗

下面将结合分类方法对生产管理模块中数据的清洗进行简单介绍：

假设选取数据库中的销售折扣数据来进行分析，假定信用等级的取值为{A，B，C}，付款方式的取值为{即付→1，预付→2，使用商业信用→3}，购买量分为两个级别{≥3000→Ⅰ，<3000→Ⅱ}，给予折扣分为五个等级{全价，9.5折，9折，8.5折，8折}，示例数据如表5413所示，验证数据集如表5-4-14所示。

表5-4-13　样本数据（用于离散值检测的训练数据）

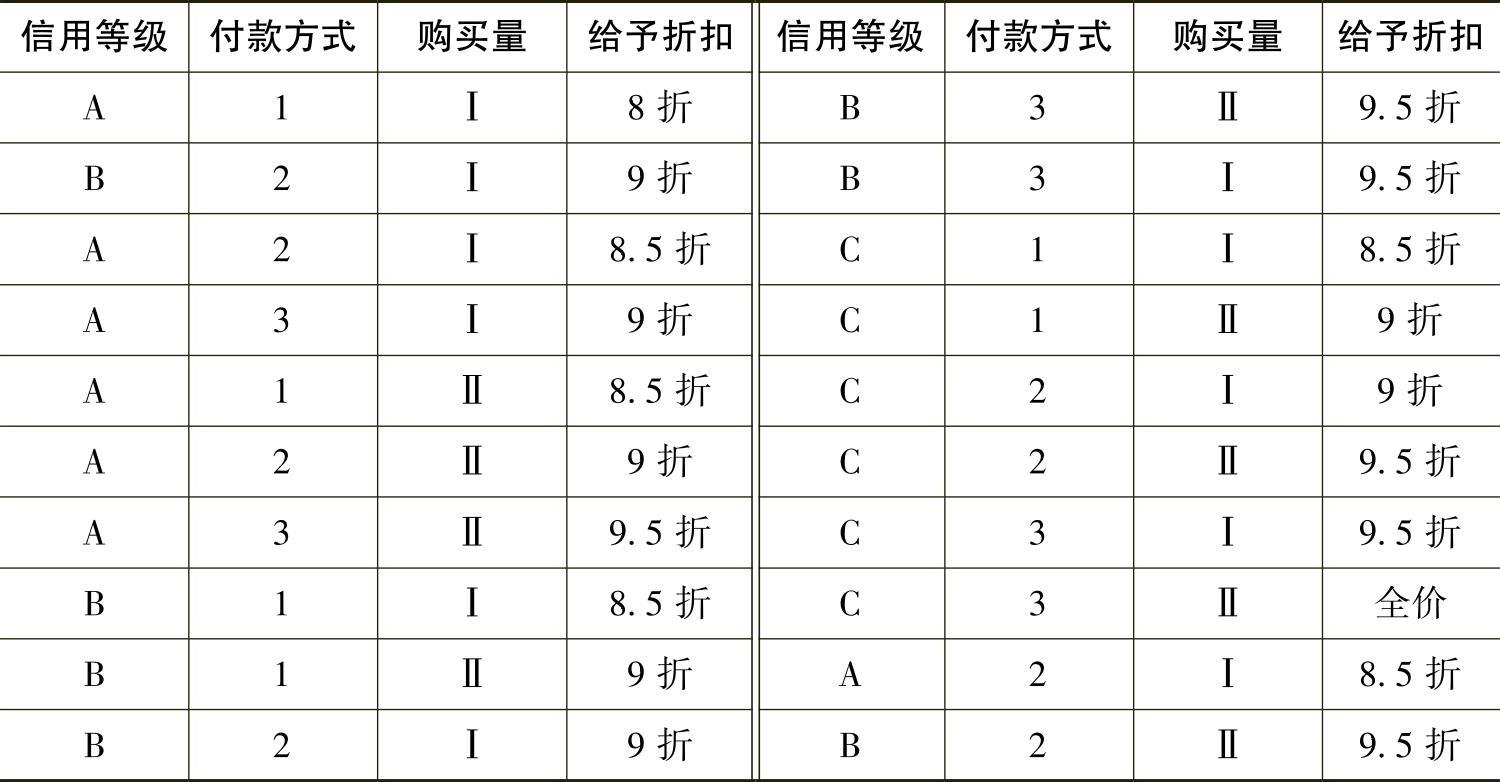
表5-4-14　待检验数据

1.决策树方法

（1）分别计算三个属性的信息增益

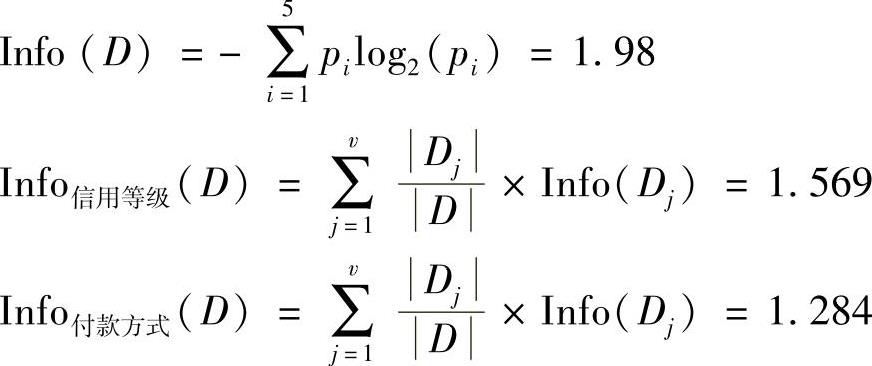
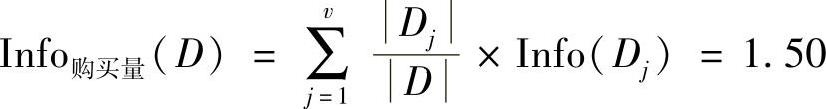
根据计算结果选择“付款方式”作为根节点，然后继续计算。(www.daowen.com)

（2）“即付”分枝的计算结果

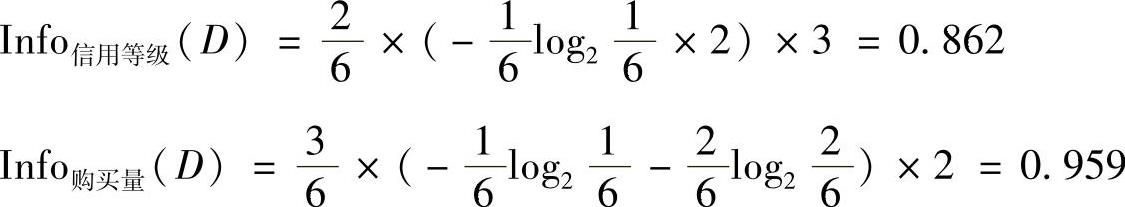
选择“信用等级”作为下一级分枝节点。

“预付”分枝的计算结果

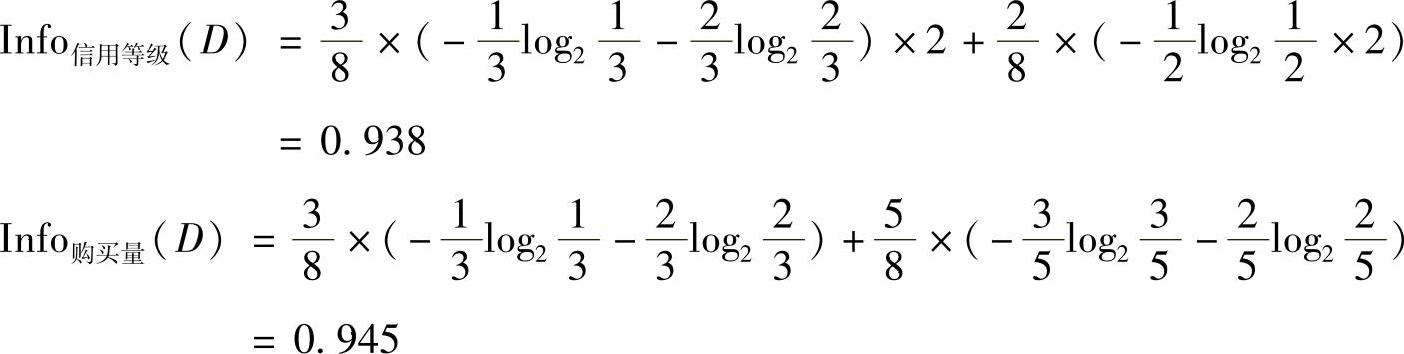
选择“信用等级”作为下一级分枝节点。

“使用商业信用”分枝的计算结果：

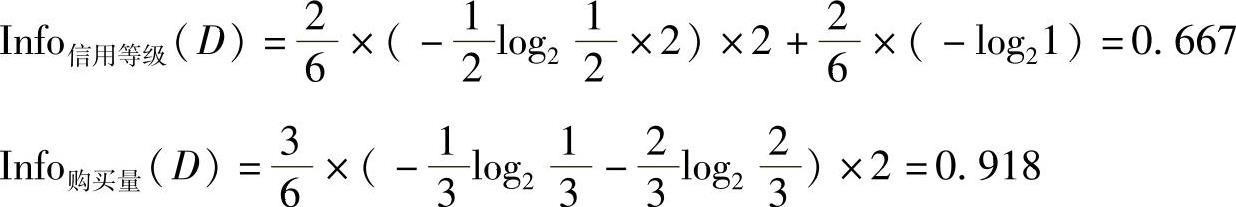
选择“信用等级”作为下一级分枝节点。

综合上述结果，绘制决策树如图546所示。

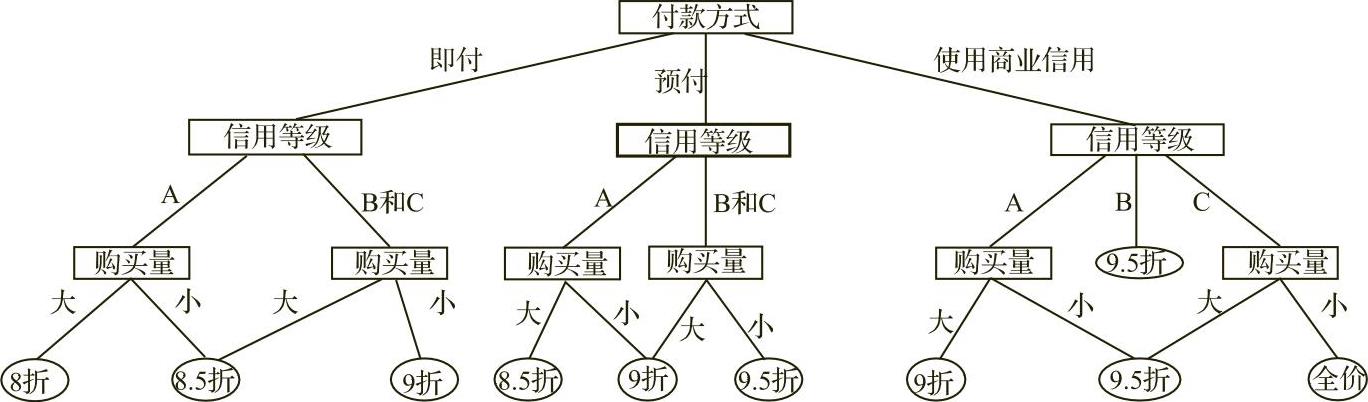
图5-4-6　构造的决策树

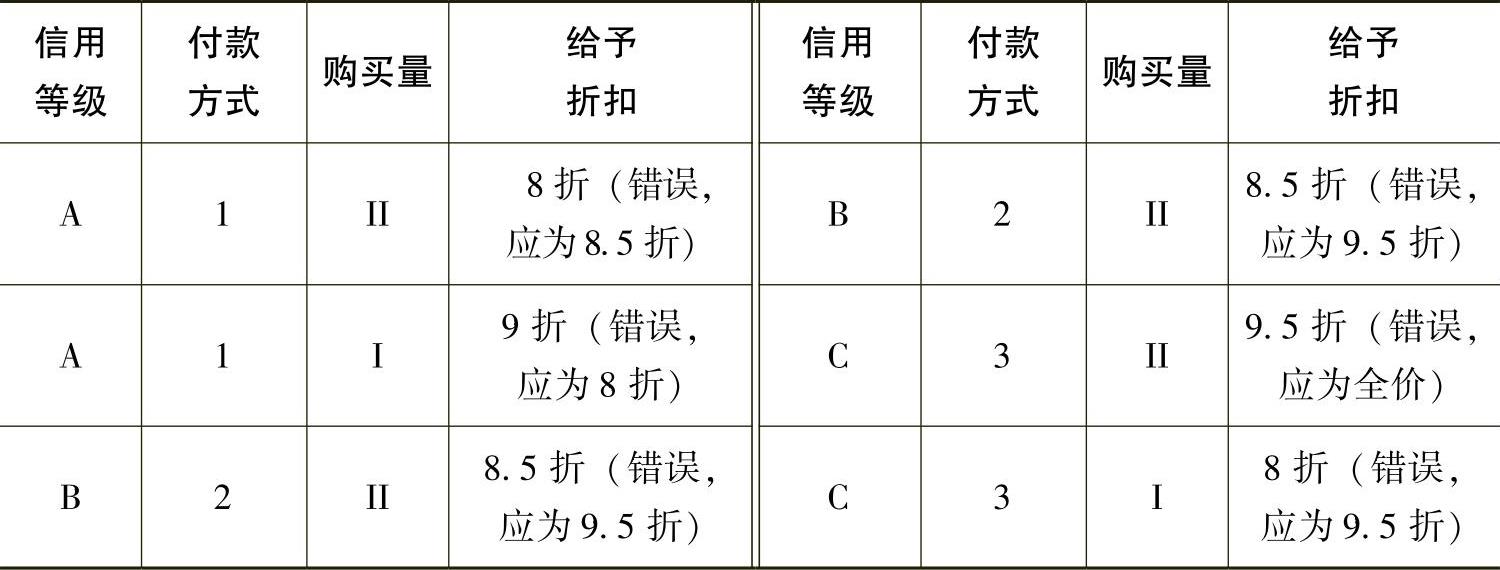
根据上述决策树，对待检验数据进行判断，结果如表5-4-15所示。

表5-4-15　判断结果

2.BP神经网络分类方法

（1）离散数据的表示

离散变量只取集合内的固定值。如一个小的类别的集合、对多重选择问题的一组响应、一组固定间隔的整数值等。对神经网络来说，离散值的表示方式要有助于神经网络区分这些离散值之间的差异，并能计算差异的大小。

为此有各种数据编码方案，下面介绍最常用的一些编码方法：

1）1/N码。当变量取一组离散值时，必须对它做某种转换，使得每一个离散值都能产生唯一的一组神经网络输入值。离散变量最常用的表示方法是1/N码。该码的长度等于离散变量中的不同类别的数目。在码向量中除了代表码值的唯一的一个元素值1外，每一元素的值均为0。例如，假设有一个含有四个元素的集合{热水器、电冰箱、电视机、微波炉}，可以将热水器表示为1000，将电冰箱表示为0100，将电视机表示为0010，将微波炉表示为0001。1/N码的优点是简单易用，神经网络很快就能学习到各个变量之间的差异。然而，对于取值数目较大的变量，就神经网络的规模来说，成本太高。

2）二进制码。另一种表示方法是采用标准的二进制码。在这种方法中，每一个离散值被赋予一个用二进制数表示的从1到N之间的值。例如，某一变量如果有32个可能的值，可用长度为5的二进制向量表示它。

只要离散值是任意的，并且没有任何的次序，二进制码就是一种较好的表示方法。然而，当离散值转换为二进制码时，其位值差别很大。例如，在一个离散类中第七个元素的二进制码是000111，而第八个元素的二进制码为001000。Hamming距离是两个二进制数之间相似性的一种度量，用两个编码中不相同码元的位数表示。那么，在这种情况下，7和8的Hamming距离为4。如果想要神经网络认为7和8这两种输入模式是相似的，就要选择温度计码。

3）温度计码。当离散值以某种方式（如增加或减少）相互关联时可采用温度计码。例如，假设有一离散变量取这样的一组离散值{差，一般，良，优秀}，在这种情况下，希望“差”和“优秀”之间的Hamming距离较大，良和优秀之间的距离较小。这时只能采用温度计码。“差”可以被表示为1000，“优秀”被表示为1111（与“差”的Hamming距离为3），“良”为1110，“一般”为1100。

当离散值以某种方式（如增加或减少）相互关联时可采用温度计码；因此，本例中BP神经网络的分类模型中，信用等级的编码占用三个输入，分别为{A⇒111，B⇒110，C⇒100}，付款方式的编码占用三个输入，分别为{即付⇒111，预付⇒110，使用商业信用⇒100}，购买量的编码占用两个输入，分别为{>3000⇒11，<3000⇒10}，给予折扣属于输出，需占用5个输出，输出编码为{8折⇒10000，8.5折⇒01000，9折⇒00100，9.5折⇒00010，全价⇒00001}，建立该分类的BP神经网络模型，输入神经元有8个，输出神经元有5个，假设隐含层有15个节点，根据下列数据进行训练。对实验数据进行转化后的数据集如表5-4-16和表5-4-17所示。

表5-4-16　转化后的实验数据集

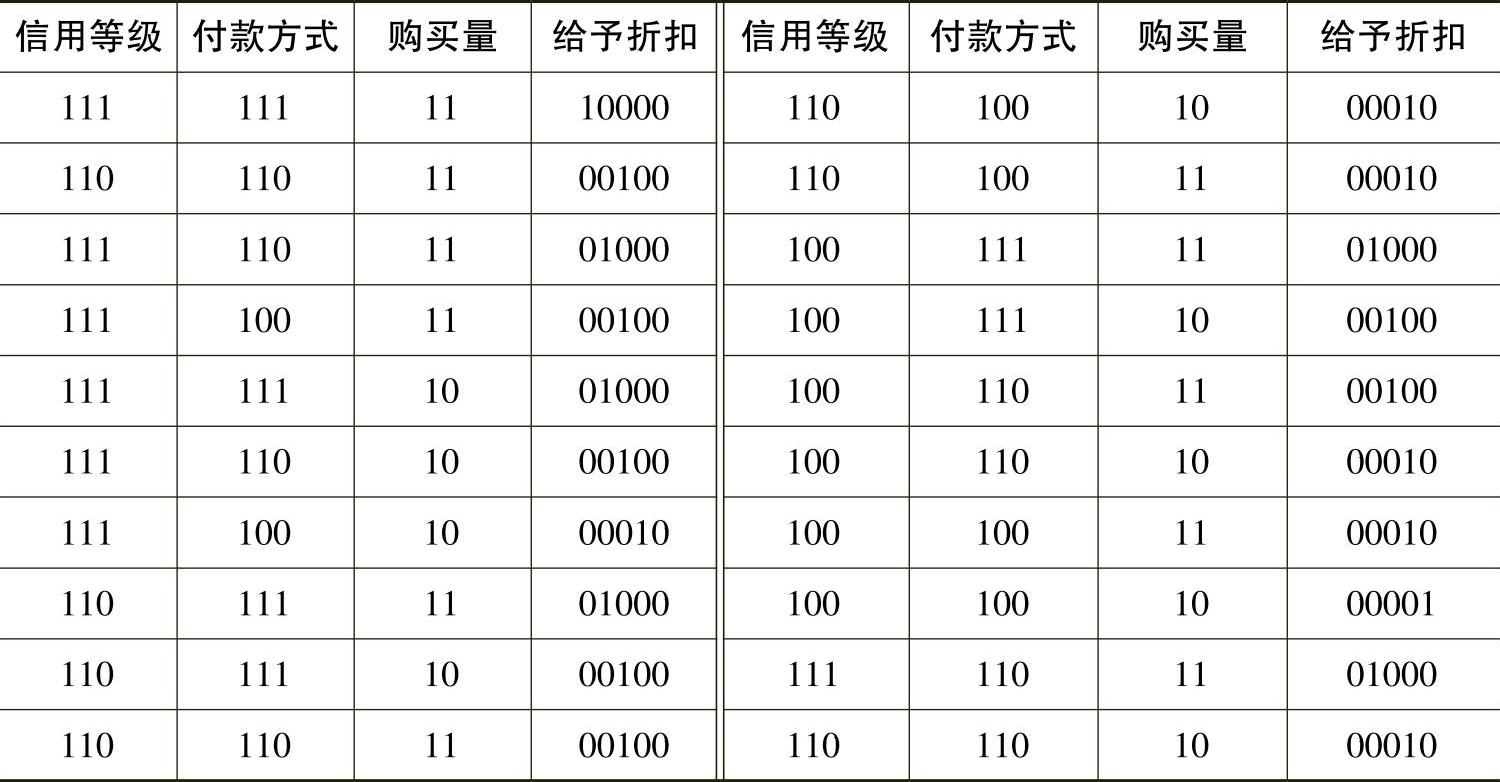
表5-4-17　转化后的待检验数据

（2）建立BP神经网络分类模型

仿真结果如表5-4-18所示。

表5-4-18　验证样本仿真结果

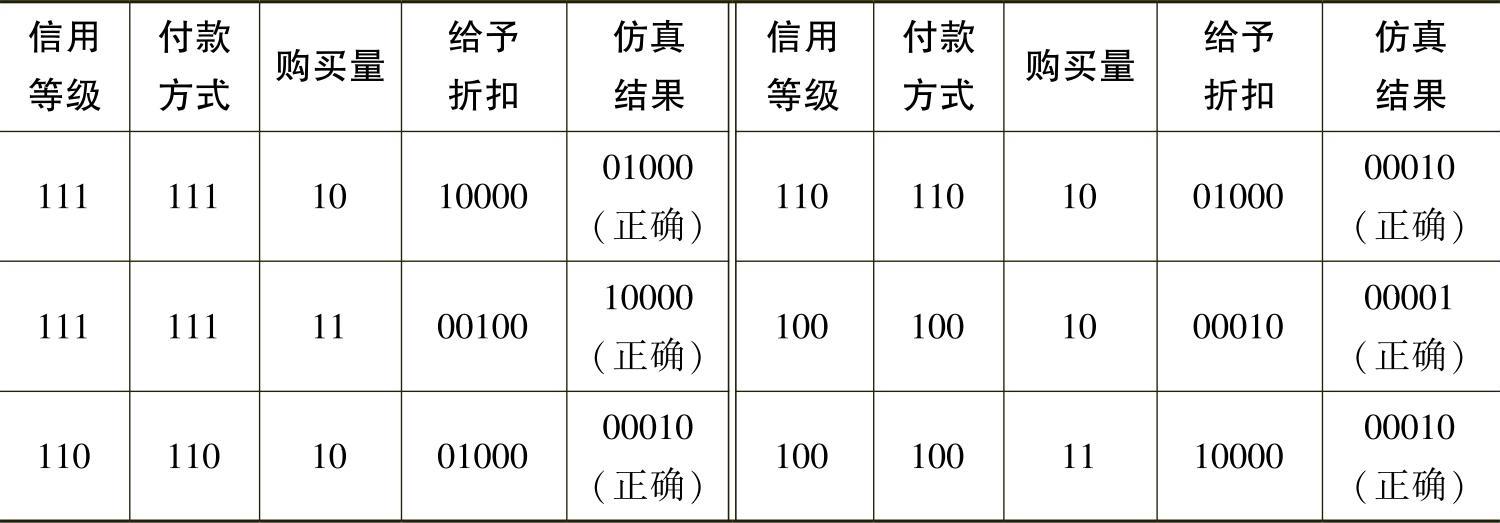
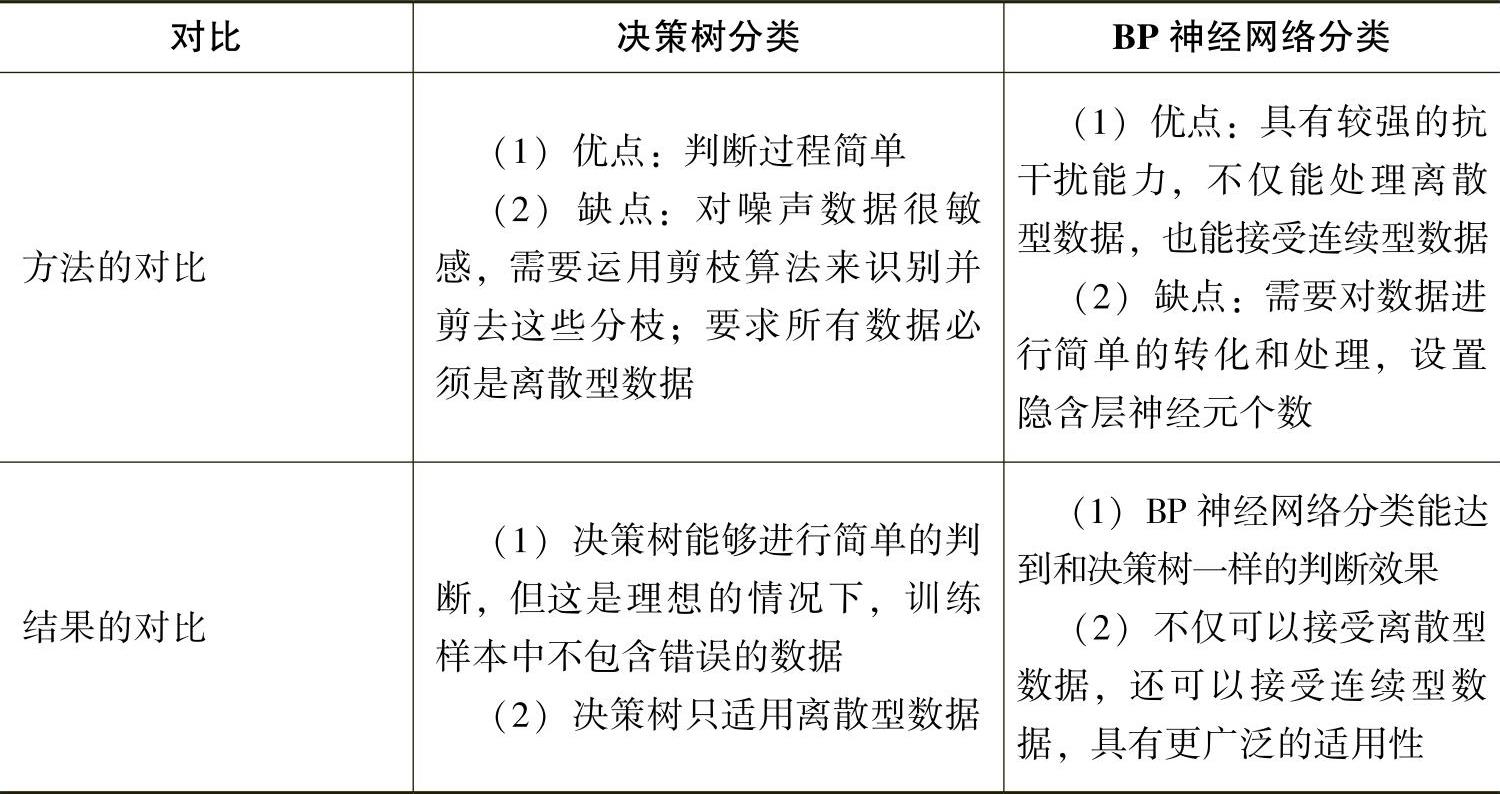
根据上述结果，两种分类方法对比如表5-4-19所示。

表5-4-19　两种分类方法的对比