（一）连续型异常数据清洗算法

1.统计型方法

统计型方法是发现异常数据的最简单方法，尤其是针对孤立点检测，比较容易实现。但是该方法也有其局限性，只能在单属性上做检测，而且要求数据的概率分布已知，但实际上大多数情况下数据分布都是未知的，这也限制了该方法的适用性。

（1）契比雪夫定理

根据属性值的期望、标准差，考虑一个数值型数据的置信区间来识别异常的记录。

定理1　契比雪夫定理

随机变量X有期望E（X）和方差D（X），则对于任意的正数ε，有

P{|X-E（X）|≥ε}≤D（X）/ε²

或P{|X-E（X）|<ε}≥1-D（X）/ε² （5-4-1）

它表明当D（X）很小的时候，X落入区间[E（X）-ε，E（X）+ε]是大概率事件。即X的概率分布集中在期望E（X）附近。

根据契比雪夫定理，使用字段值的平均值、标准差，考虑每一个字段的置信区间来识别异常的字段和记录。如一个字段f_i可以看做是一个随机变量，该变量的取值个数与在该字段有值的记录的数目是相同的。考虑字段的置信区间，如果f_i的值大于μ_i+εσ_i或f_i的值小于μ_i-εσ_i，则记录r_j中的字段f_i被认为是一个孤立点，其中μ_i是字段f_i的均值，σ_i是标准差，ε是由用户定义的因子，可分别取3，4，5，6几个值，ε的值可以基于某些领域知识或数据知识来由用户定义或应用契比雪夫定理从理论上定义。

（2）盒图

一种流行的可视化表示是盒图（BoxPlot）。盒图体现了五数概括，即由中位数、四分位数Q₁和Q₃、最小值和最大值组成，按次序写为min，Q₁，median，Q₃，max。

盒图按照如下要求绘制：

1）中位数用盒内的线来标记。

2）盒的两个端点在四分位数Q₁和Q₃处，使得盒的长度为IQR。

3）盒外的两条线分为以下两种情况：仅当min和max的值超过四分位数不到1.5×IQR时，则须扩展到最高和最低观测值；否则，胡须出现在四分位数的1.5×IQR之内的最极端的观测值处终止。

给出一个简单的例子：商品A的销售数据的特征如下：median=1000，Q₁=850，Q₃=1150，min=300，max=2000，IQR=300，Q₁-1.5IQR=850-450=400，Q₃+1.5IQR=1150+450=1600。

由于min和max的值超过四分位数达到1.5×IQR处，所以，胡须不能扩展到最高和最低观测值，假定在[400，1600]范围内极端的观测值为400和1600，那么胡须向下扩展到400，向上扩展到1600，如图5-4-1所示。

一个识别可疑的孤立点的常用经验是：挑出落在至少高于第三个四分位数或低于第一个四分位数1.5×IQR处的值。

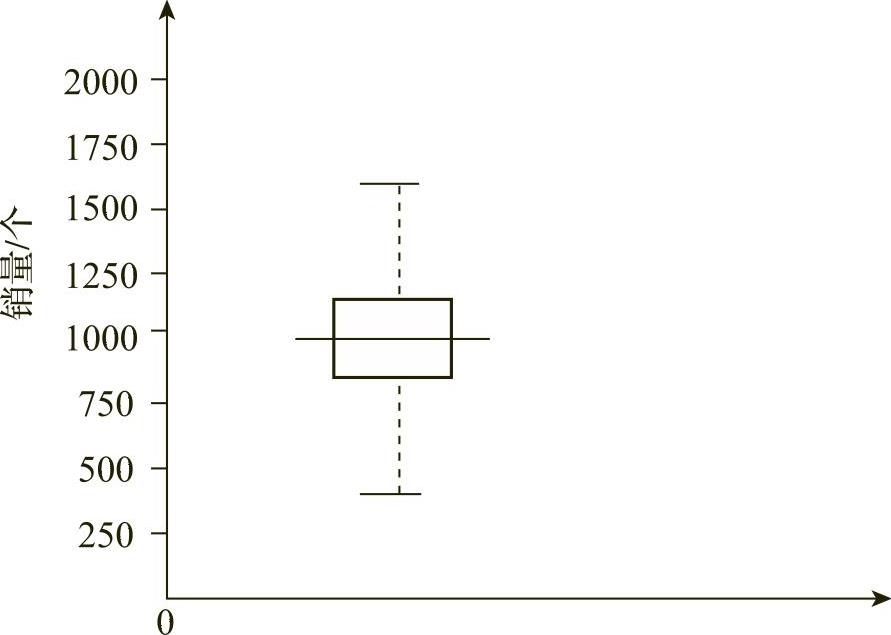
图5-4-1　盒图举例

2.聚类型方法

聚类是将数据对象分成类或簇的过程，使同一簇中的对象之间具有很高的相似度，而不同簇中的对象高度相异。聚类算法大体上分为基于划分的方法、基于层次的方法、基于密度的方法、基于网格的方法和基于模型的方法以及模糊聚类。

k均值方法是最具有代表性的基于划分的聚类方法，SOM聚类方法也是最常见的基于模型的方法，所以本章中将这两种方法应用到生产管理模块的数据清洗中，并进行对比分析。

（1）k均值聚类方法

k均值算法以k为输入参数，把n个对象的集合合成为k个簇，使得簇内相似度高，而簇间的相似度低。簇的相似度是关于簇中对象的均值度量，可以看作簇的质心或重心。

k均值算法的处理流程如下：首先，随机地选择k个对象，每个对象代表一个簇的初始均值或中心。对剩余的每个对象，根据其与各个簇均值的距离，将它指派到最相似的簇。然后计算每个簇的新均值。这个过程不断重复，直到准则函数收敛，通常采用平方误差准则，其定义如下：

其中E是数据集中所有对象的平方误差和，p是空间中的点，表示给定对象，m_i是簇C_i中的均值。

（2）基于SOM的聚类方法

自组织映射网络（Self-Organizing Map，SOM）是由芬兰赫尔辛基大学神经网络专家Kohonen于1981年提出的，这种网络模拟大脑神经系统自组织特征映射的功能。

SOM的网络结构如图5-4-2所示。输入层的神经元数为N，竞争层是由M=m²个神经元组成，且构成一个二维平面阵列，输入层与竞争层之间实现全互连接，有时竞争层各神经元之间还实行侧抑制连接。网络中有两种连接权值，一种是神经元对外部输入反应的连接权值，另一种是神经元之间的连接权值，它的大小控制着神经元之间的交互作用的大小。

自组织特征映射算法是一种无教师示教的聚类方法，它能将任意维输入模式在输出层转化成一维或二维离散图形，并保持其拓扑结构不变，即在无教师示教的情况下，通过对输入模式的自组织学习，在竞争层将分类结果表示出来。

设自组织神经网络的输入模式为P_k=（p^k₁，p₂^k，…，p^k_N），k为训练样本数，k=（1，2，…，q）。竞争层神经元矢量为A_j=（a_j1，a_j2，…，a_jm），j=1，2，…，m；其中P_k为连续值，A_j为数字量。竞争层神经元j与输入层神经元之间的连接权矢量为W_j=（w_j1，w_j2，…，w_jN），i=（1，2，…，N）；j=（1，2，…，M）。

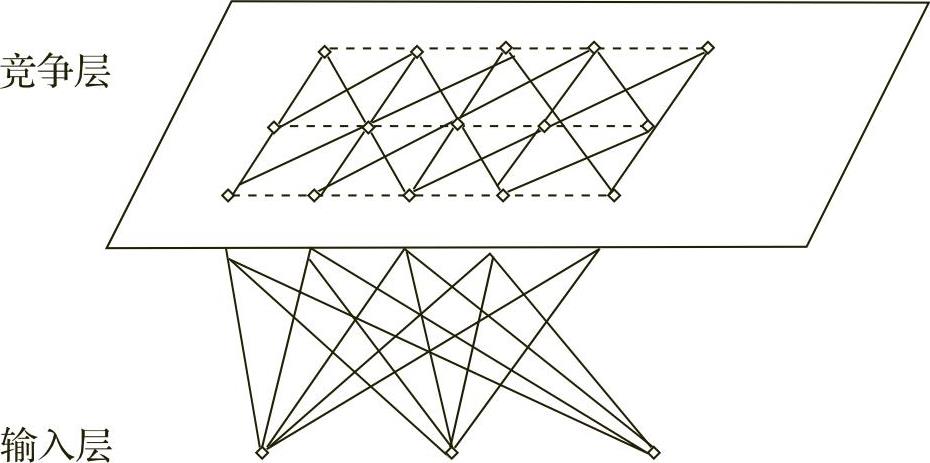
图5-4-2　自组织特征映射网络结构[54]

Konohen网络的自组织学习过程可以描述为：对于每一个网络的输入，只调整一部分权值，使权向量更接近或更偏离输入矢量，这一调整过程就是竞争学习。随着不断学习，所有权矢量都在输入矢量空间相互分离，形成了各自代表输入空间的一类模式，这就是Konohen网络的特征自动识别的聚类功能。

网络的学习及工作规则为：

1）初始化。将网络的连接权{w_ij}赋予[0，1]区间内的随机值。确定学习率_η（t）的初始值η（0）（0<η（0）<1）；确定邻域N_g（t）的初始值N_g（0）。邻域N_g（t）是指以步骤4）确定的获胜神经元g为中心，且包含若干神经元的区域范围。这个区域一般是均匀对称的，最典型的是正方形或圆形区域。N_g（t）的值表示在第t次学习过程中邻域中所包含的神经元的个数；确定总的学习次数为T。

2）任选q个学习模式中的一个模式P_k提供给网络的输入层，并进行归一化处理。

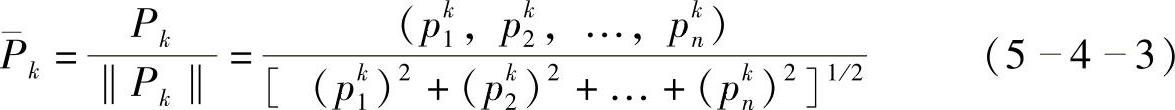
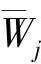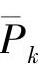3）对连接权矢量W_j=（w_j1，w_j2，…，w_jN）进行归一化处理，计算与之间的欧式距离。

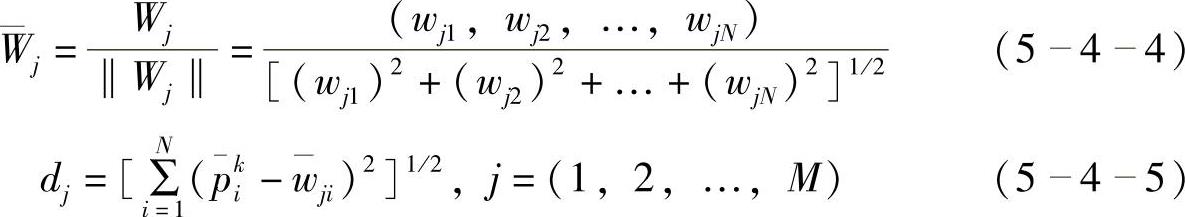
4）找出最小距离d_g，确定获胜神经元g。

d_g=min[d_j]，j=（1，2，…，M） （5-4-6）

5）进行连接权的调整，对竞争层邻域N_g（t）内所有神经元与输入层神经元之间的连接权进行修正。

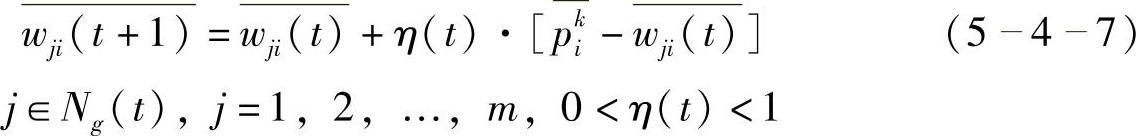
6）选取另一个学习模式提供给网络的输入层，返回步骤c），直至q个学习模式全部提供给网络。

7）更新学习率η（t）及邻域N_g（t）

其中_η（0）为初始学习率，t为学习次数，T为总的学习次数。

假设竞争层某神经元g在二维阵列中的坐标值为（x_g，y_g），则邻域的范围是以点（x_g+N_g（t），y_g+N_g（t））和（x_g-N_g（t），y_g-N_g（t））为右上角和左下角的正方形。其修正公式为

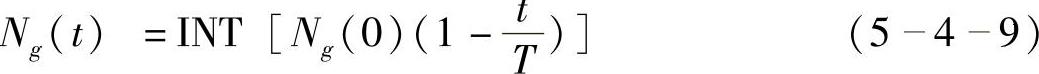
式中INT[x]为取整符号，N_g（0）为N_g（t）的初始值。

8）令t=t+1，返回步骤b），直至t=T为止。

（3）预测型方法

最常见的预测模型就是回归分析，但回归分析仅适用于线性模型，另外一种常用的预测模型就是BP神经网络，不仅可以处理连续型数值，也可以用来处理离散型数值，而且可以逼近任意的非线性函数，具有更广阔的应用空间。

1）回归预测

回归分析可以用来一个或多个独立或预测变量和一个（连续值的）依赖或响应变量之间的联系建模。在数据检测和清洗中，我们将预测变量的值与实际存储值进行对比分析，判断其是否为正确值。

2）BP神经网络预测

常见的用于预测的神经网络模型如图5-4-3所示，它由输入层、隐含层和输出层构成。由于是用于预测，所以输出层只有一个节点。

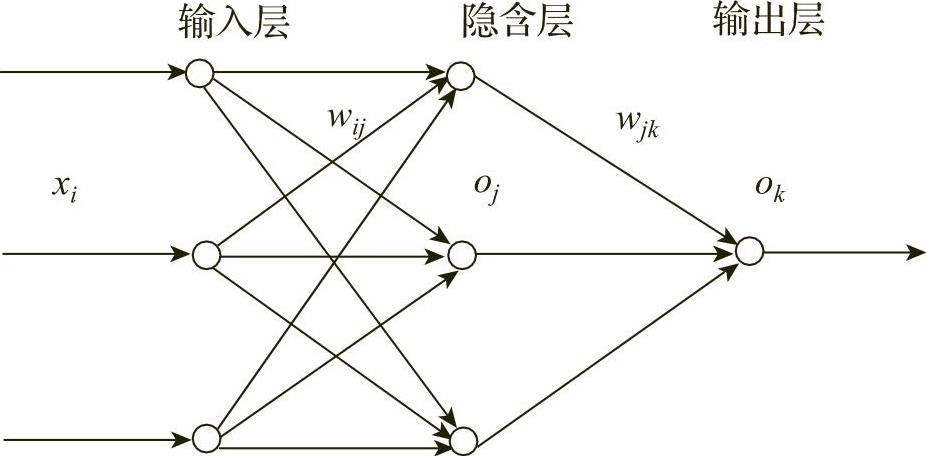
图5-4-3 BP神经网络的预测模型(www.daowen.com)

用BP神经网络的后向传播迭代地处理训练元组数据集，将每个元组的网络预测与实际已知的目标值进行比较，对于每个训练样本，修改权重使网络预测和实际目标值之间的均方误差最小。算法流程如图544所示。

变量l是学习率，通常取0.0～1.0之间的常数值。后向传播学习使用梯度下降法搜索权重的集合。这些权重拟合训练数据，使网络预测与元组的已知目标值之间的均方距离最小。学习率帮助避免陷入决策空间的局部极小，并有助于找到全局最小。如果学习率太小，学习将进行得很慢。如果学习率太大，可能出现在不适当的解之间摆动，一个经验法则是将学习率设置为1/t，t是当前训练集迭代的次数。

如果前一周期所有的Δw_ij都小于某个指定的阈值，或超过预先设定的周期数，训练终止。

图5-4-4 BP神经网络用于分类和预测的算法流程

（二）数据不准确性改善在生产管理模块中的应用

在生产管理系统中，连续型数值异常数据的表现形式如表541所示，并指出了相应的检测和清洗方法。

表5-4-1　连续型数值异常数据的检测和清洗

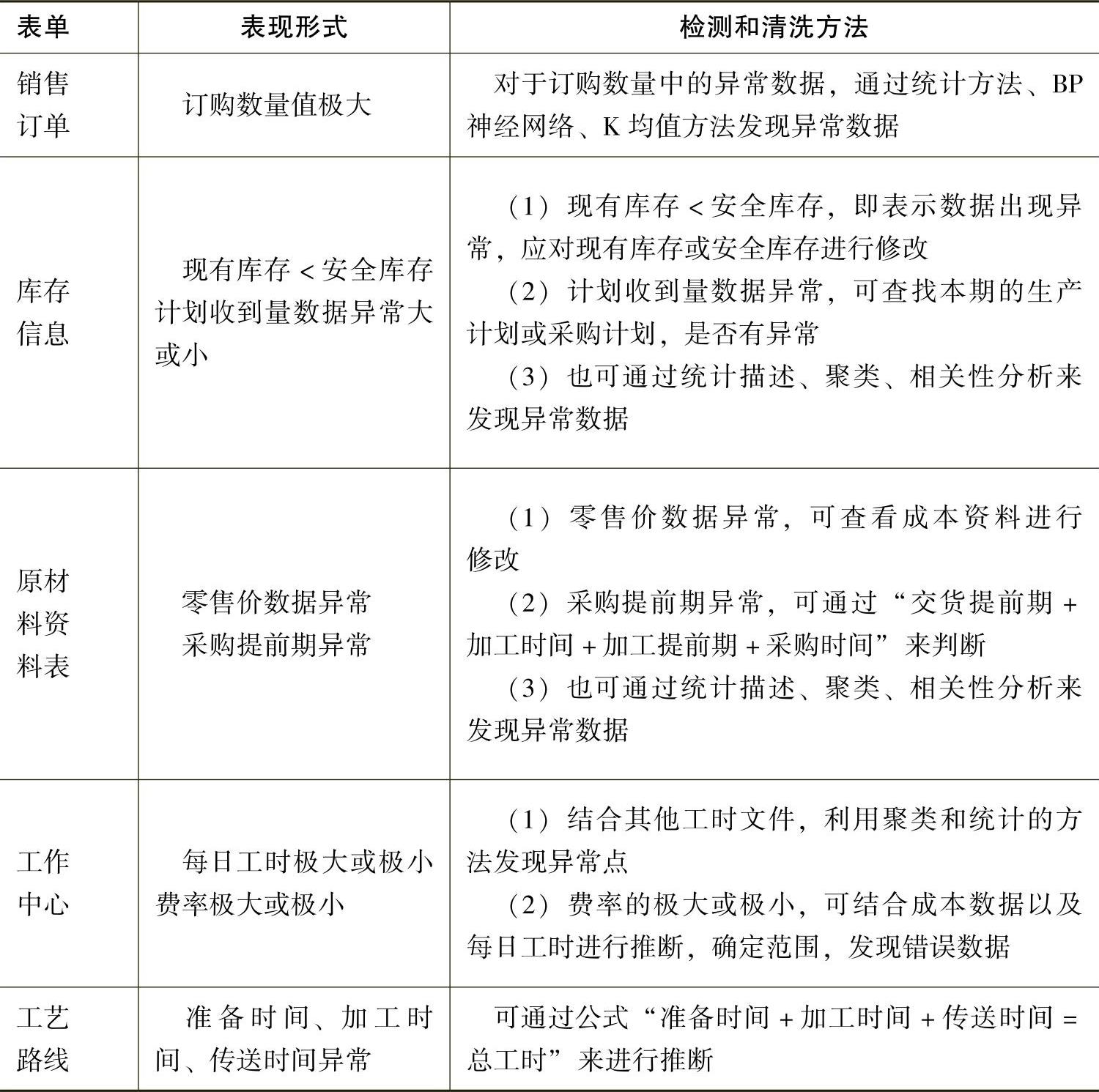
一般而言，连续型数值数据的检测流程分为以下几个步骤：

1）描述数据库中单个字段的基本统计信息，如均值、方差；通过契比雪夫定理，找出超出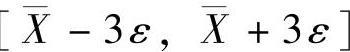范围的异常值；或通过公式，计算数据的中位数、第一个四分位数和第三个四位数，并绘制盒图，发现孤立点。

2）通过相关属性的关系图，发现其中的异常数据组合，如通过单价和订购数量的组合发现异常记录。

3）为了更准确地预测数据的范围，发现更多的异常数据，可以通过BP神经网络模型对数据进行预测，确定相应的误差范围，超出范围的数据即为异常数据。

4）建立SOM神经网络模型，不仅可以针对单个属性值的聚类，也可以对相关的多个属性进行聚类，发现“自成一类”的数据，即为异常数据或异常数据组合。

对于发现的异常数据，可通过以下方法进行清洗：①查找相关原始资料修改数据。②利用相关运算进行修改，如“采购提前期”。③利用比率关系（如单价和销售量）来进行修改。

下面将结合聚类和预测方法对生产管理模块清洗进行简单说明。

1.聚类方法

我们以数据库中销售订单数据为例，一般而言相同客户一段时期内的购买量基本上是相同的，而不同客户之间可能差异较大，对不同客户的购买量数据进行聚类，以发现一些异常数据。示例数据如表5-4-2所示。

通过K均值聚类和SOM聚类方法在示例数据中的应用，可以发现示例数据中存在的异常数据，并对两种方法进行对比分析。

表5-4-2　示例数据表

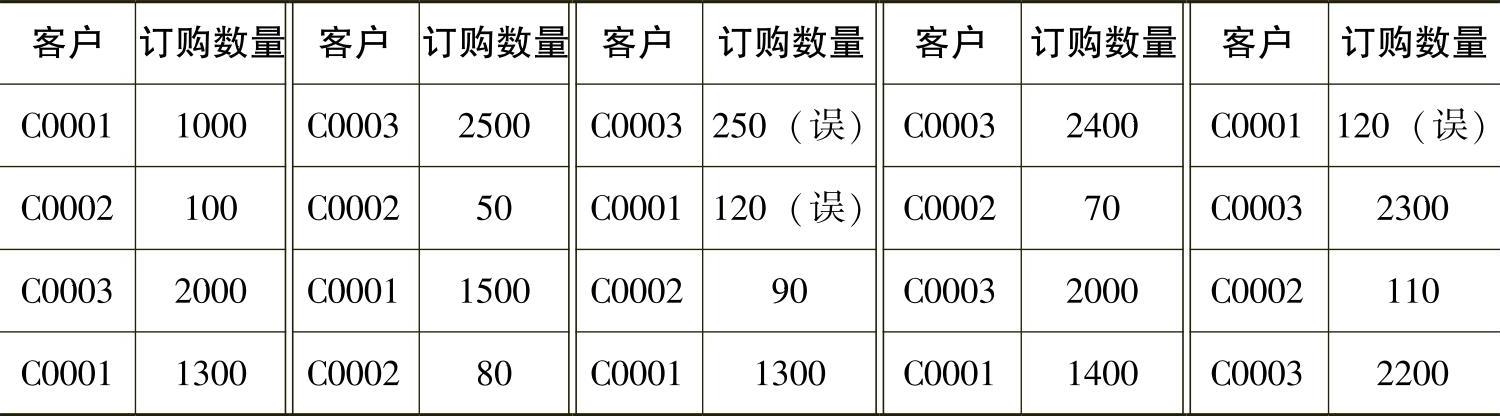
（1）k均值聚类

表中一共涉及三个供应商，将聚类数目设为3，然后使用SPSS软件包对其进行分析。结果如表5-4-3所示。

表5-4-3　k均值聚类的结果

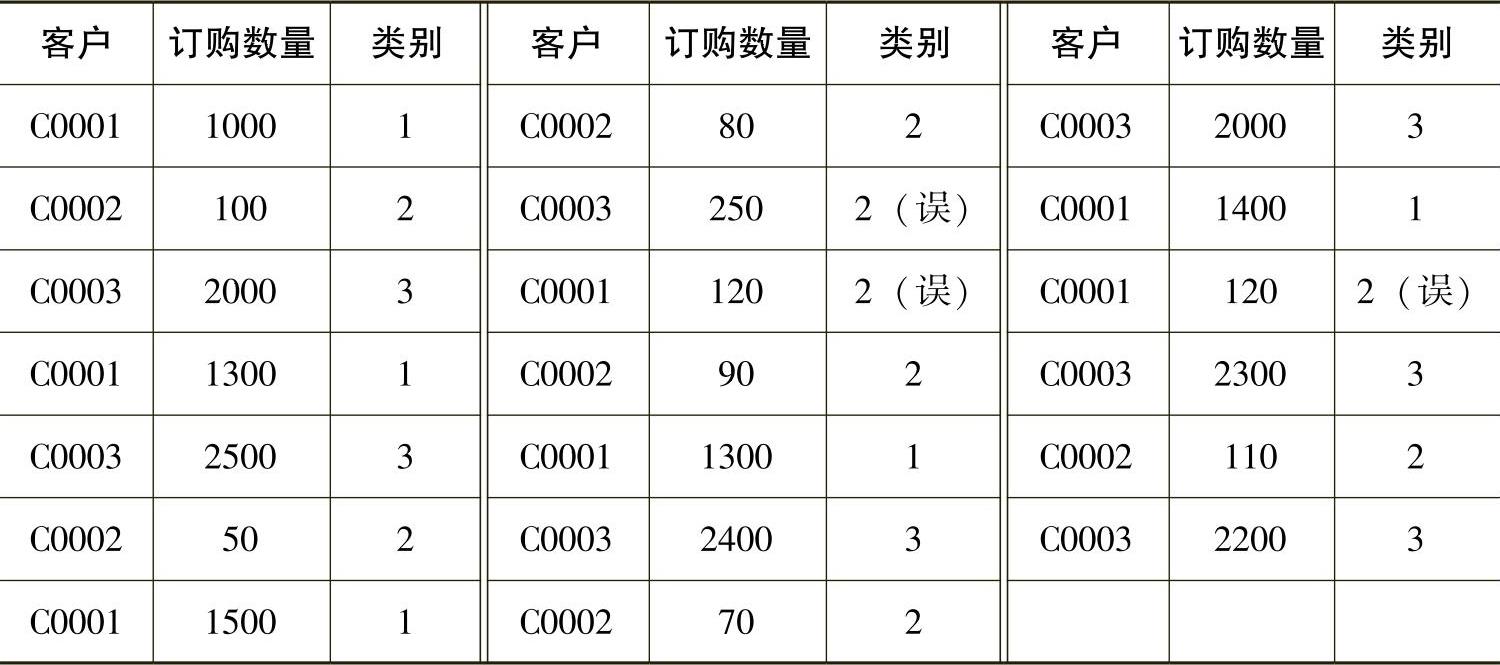
通过K均值聚类，我们发现了数据表中存在的错误数据，这是在一种比较理想化的情况下，K均值聚类方法对噪声数据的敏感性以及种种缺陷也限制了它的广泛应用。

（2）SOM聚类

建立SOM网络的聚类模型，由于只有三个供应商的订购数量记录，所以将输出层的神经元数设为3。输入数据只有1个神经元，即订购数量。通过Matlab中程序的运行，SOM网络聚类的结果如表5-4-4所示。

表5-4-4 SOM网络聚类运行结果

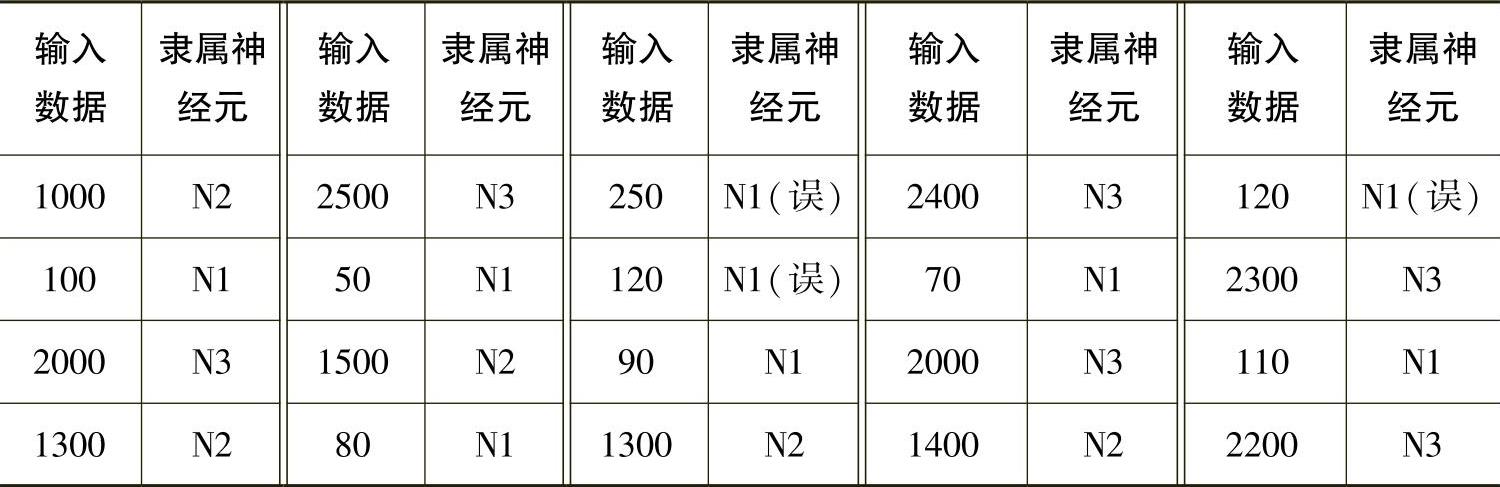
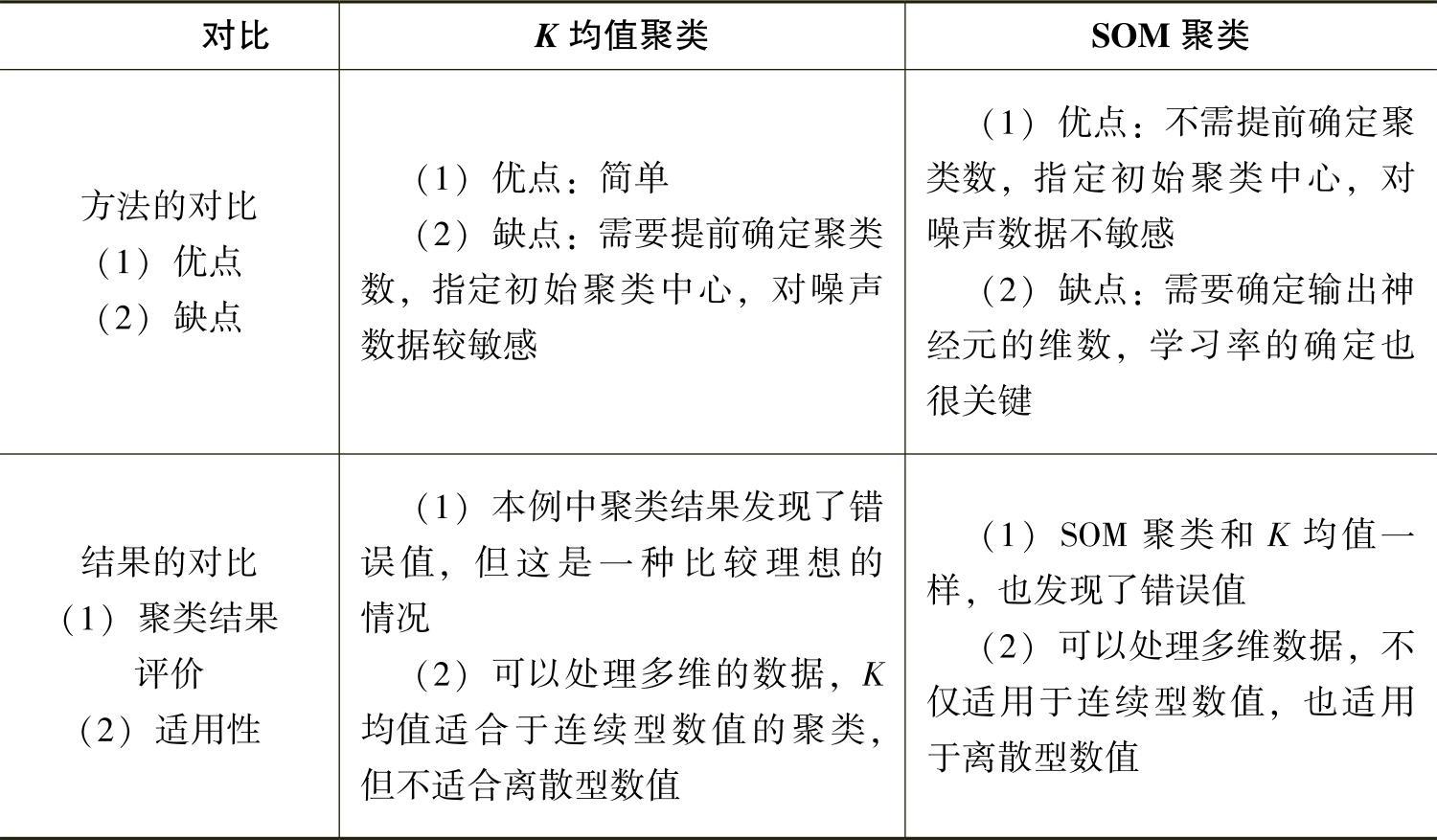
对比上述分析结果，并参考其他资料，将K均值聚类和SOM网络聚类方法进行比较，结论如表5-4-5所示。

表5-4-5　两种聚类方法在生产管理模块中应用结果的对比

2.预测方法

我们以数据库中销售订单的订购数量为例进行分析，一般而言，一个客户的购买量一般是连续的，且在一定期间内不会发生太大的变化，那么如果发现变化较大的数值就说明该数据可能存在错误，或者是发生了一些异常情况，需要具体分析。

表5-4-6给出了客户C1在一段时期内的购买量的数据，然后判断表5-4-7中的数据是否是正确的。

表5-4-6　客户C1一段时间内的购买量

表5-4-7　需要判断的数据表

（1）回归分析预测

线性回归的目的是建立多个变量之间的线性关系。以多元回归为例，它允许响应变量y用描述元组x的n个预测变量或属性A₁，A₂，…，A_n的线性函数建模（即X=（x₁，x₂，…，x_n））。训练数据集D包含形如（X₁，y₁），（X₂，y₂），…，（X_|D|，y_|D|），其中X_i是n维训练元组，具有相关联的响应变量值y_i。最终多元线性回归的模型如式（5-4-10）所示。

y=w₀+w₁x₁+w₂x₂+…+w_nx_n （5-4-10）

假设建立的预测模型是x_n=w₃x_n-1+w₂x_n-2+w₁x_n-3+w₀，利用统计软件SPSS对上述数据进行回归，得到

x_n=456.320+0.425×x_n-3-0.828×x_n-2+0.760×x_n-1

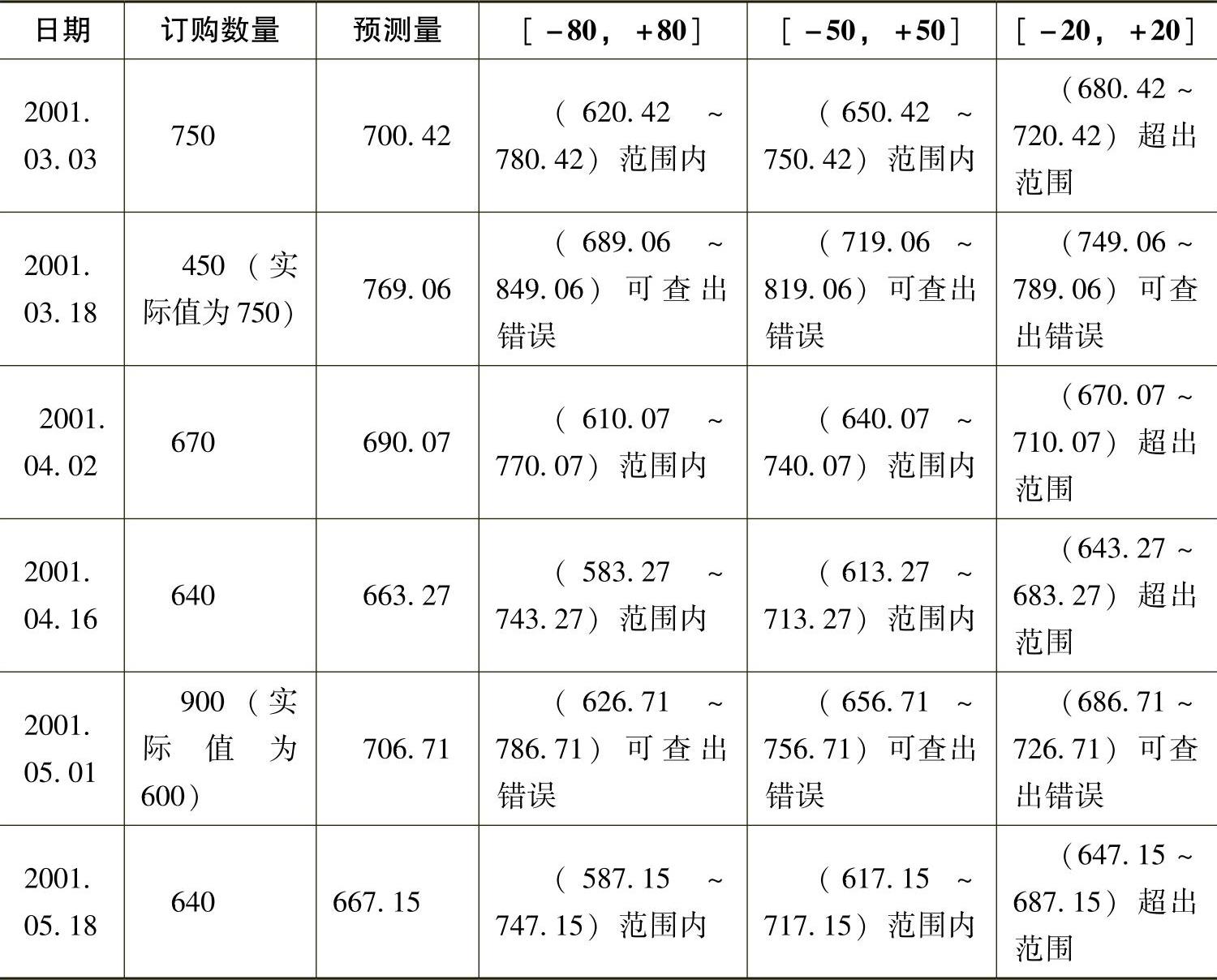
根据上述回归分析的结果，得出预测结果如表548所示。我们假定预测结果值的限定范围为[-80，+80]区间内都为合理的。

表5-4-8　判断结果

（2）BP神经网络预测

根据训练表以及验证表的数据，确定订购量中数据的取值范围为[450，900]。根据神经元激励函数的不同，大多数神经网络只接受[0.0，1.0]和[-1.0，+1.0]范围的数值数据。因此，数据必须按比例缩小到这个区间内。连续型数值数据基本上均匀地分布在某一范围内，可以直接映射到区间[0.0，1.0]。若数值数据分布不均匀，可用分段线性方程或对数方程对数据进行转换，然后再按比例缩小到指定区间。

例如，一个在取值范围为[0，1000]的变量可以通过线性比例变换映射为区间[0.0，1.0]。这样，200就变成了0.2，而750变成了0.75。对于像这样均匀分布的变量来说，简单的线性变换就足够了。

当数据分布不均匀时，问题就变得稍微复杂起来。一种选择就是采用分段线性变换方法对数据进行比例变换。采用这种方法，神经网络认为输入数据差别较大，因此就能比较容易地区分输入数据的差异。值得一提的是，如果输入值的差别较小，但又比较重要，则必须保证将这种重要性让神经网络知道。

例如，假设80%的数据小于500，并且想要神经网络较好地区分0～500范围内的数据，采用分段线性变换方法对数据进行比例变换，这样，0～500范围内的数据会被放大，而不太重要的500～1000输入范围内的数据则被压缩。通过采用0、500、1000的输入范围和0.0、0.8、1.0这样的映射区间就可以做到。在这种情况下，输入值500将被赋予0.8，而750应设置为0.9，这样，相差250的输入值经过转换后神经网络认为其差异为0.1，而输入时为100的数转换为0.16，输入时为250的数转换后则为0.4，这时，神经网络认为输入数据差别较大，因此就能比较容易地区分输入数据的差异了。

另一种常用的方法是设置阈值。例如，假设收入范围是[0，30000]元人民币。但若检查某个人的收入是否超过了35000元。可以简单地设置收入阈值，对于那些0～30000元范围的值，由于没有达到阈值，将它比例变换到[0，1]内，超过35000元的值则到达阈值35000元，这样可取值1。由于并不关心这个变量的整个取值范围，也就没必要让神经网络去区分这个差别。

根据上述的连续型数值的处理，采取比例转换法将数据映射到区间[0，1]，处理结果如表5-4-9所示。

表5-4-9　处理后的数据

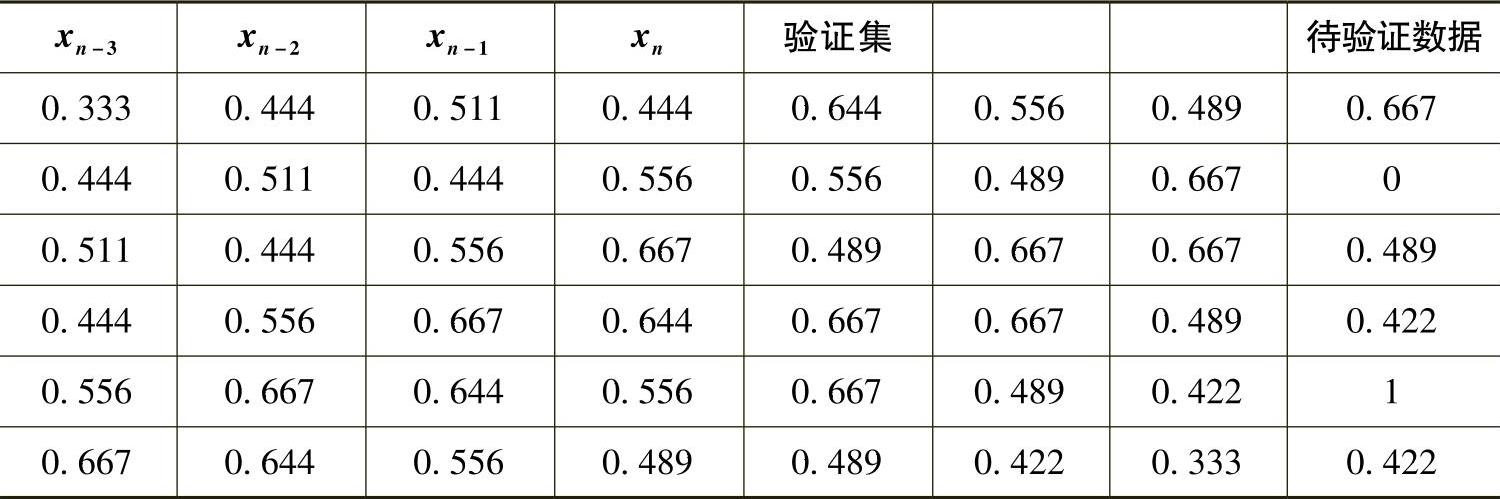
本节中选择基于LM改进的BP神经网络，通过Matlab 6.5实现，得到的验证结果如表5-4-10所示。输入神经元数为3个，隐含层神经元数为12个，输出层为1个神经元。

表5-4-10 BP神经网络预测的结果

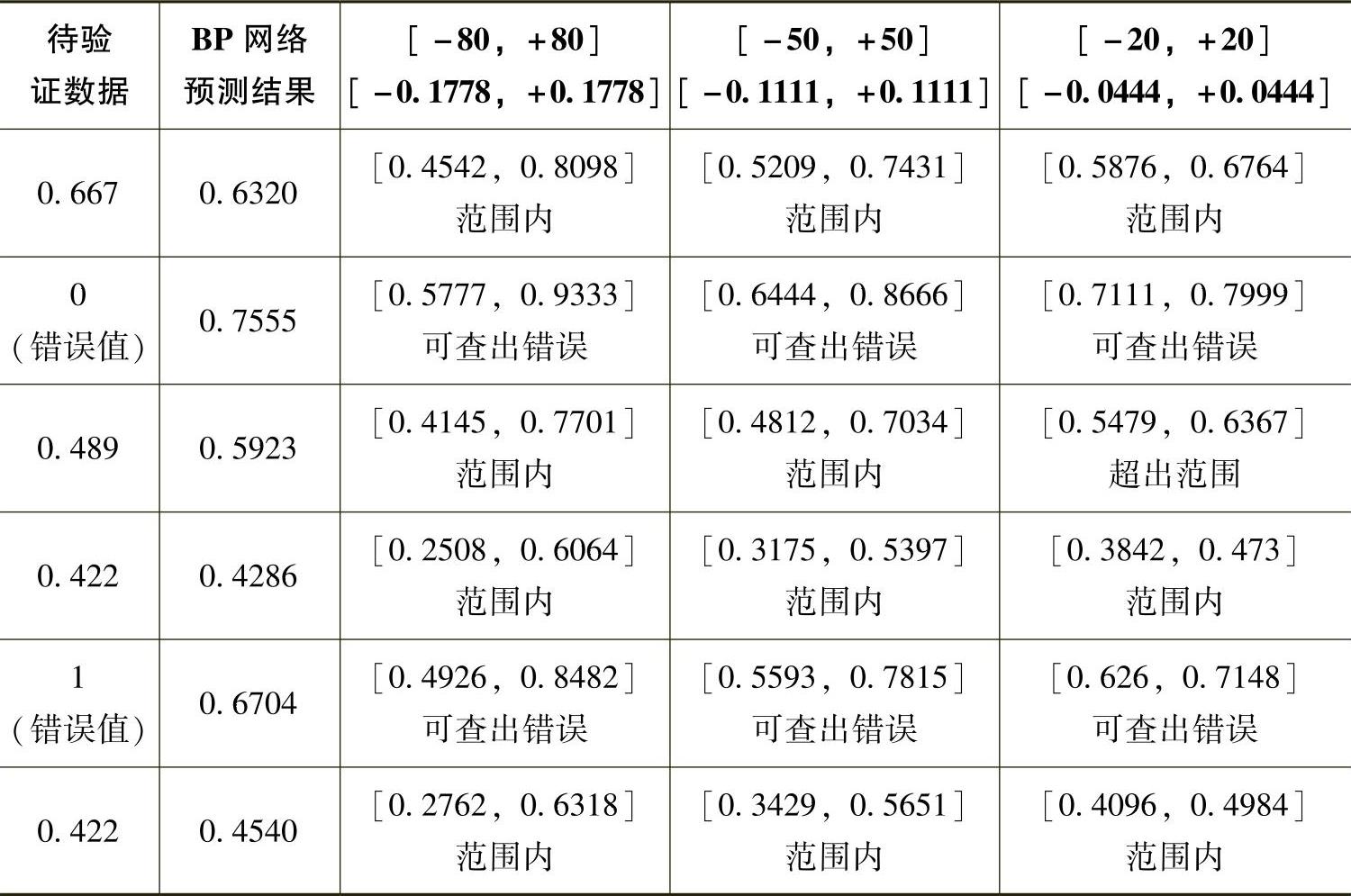
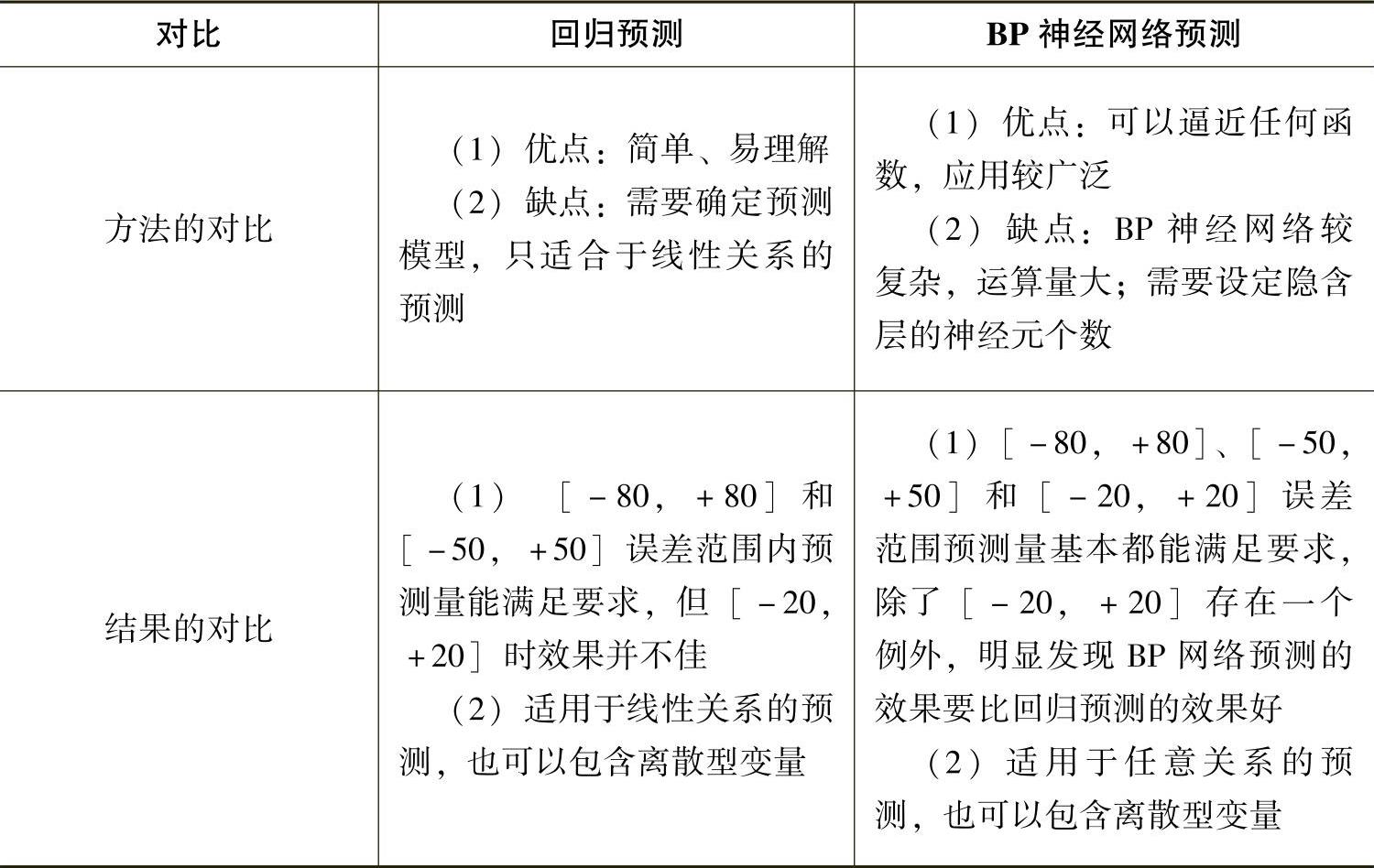
对比上述分析结果，以及参考其他资料，将回归分析和BP神经网络预测进行比较，结论如表5-4-11所示。

表5-4-11　两种预测方法在生产管理模块中应用结果的对比