（一）求解0-1整数规划的一般方法

0-1型整数规划是一种特殊形式的整数规划，它的决策变量x仅取两个值0或1，故x称为0-1变量，或称二进制变量。0-1型整数线性规划的数学模型一般是这样的：

目标函数

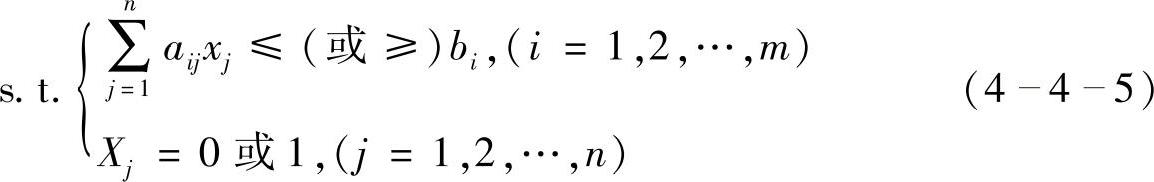
对于0-1型整数规划问题，由于每个变量只取0，1两个值，人们自然会想到用穷举法来解，即排出全部决策变量取值为0或1的每一种组合，算出目标函数在每一组合（点）上的函数值，找出最大（最小）值可求得问题的最优解，这样，就需要比较目标函数在2ⁿ个组合（点）上的取值大小，对于变量个数n较大时，这种方法即使用现代的大型计算机来计算也是不可取的。因此，常设计一种算法，只需比较目标函数在一小部分排列组合（点）上取值的大小，而根据一定的判别法则舍去不包含最优解的排列组合，就能求出问题的最优解。这样的方法称为隐枚举法。

1.隐枚举法Ⅰ

过滤隐枚举法是一种特殊的分枝界定法。这种方法是从某一可行解（决策变量组合）出发，确定一个目标值。然后，通过对决策变量的改进，形成新的变量组合。当新的变量组合的目标值小于先前的目标值并满足所有约束条件要求时，就用新目标值替代先前的目标值，否则，舍去这组变量组合。重复这种方法，通过隐含枚举，直到可行域内的所有可能的变量组合皆被筛选过。隐枚举法的特点是只检验变量组合的一部分，就能求得问题的最优解或满意解，与穷举法相比，大大减少了枚举次数。

该法的主要步骤为：

1）先通过试算获得一个初始可行解，求得对应此可行解的初始目标函数值minz（或者maxz），称minz（或者maxz）为此整数规划问题的一个初始闭值（门槛值）。

2）然后按照决策变量的字典序列给出第二个解（不一定是可行解），计算目标函数值Z，若Z>minz，（或者Z<maxz）则不必判断是否满足约束条件（是否可行解），阈值仍为minz或maxz；若Z<minz，（或者Z>maxz）则判断此解是否可行，如果是可行解，则阈值变为z，若是非可行解，则闭值仍为minz（或者maxz），若z=minz（或者maxz），则阈值仍可取为minz（或者maxz）。

3）接下来返回2）继续重复该步骤，便可求得目标函数z最小或者最大时的可行解。

2.隐枚举法Ⅱ

隐枚举法Ⅱ此类解法的特点是先把数学模型改造为标准型，然后按一定顺序检验解集中各解的可行性，力争只检验较少的解便找到最优解。此类解法对标准型的要求基本相同，但在确定检验顺序上有不同的处理，大致分为两种：一种是借用求解整数规划的分枝定界法的思路，将检验的解点排列成树枝状，称为隐枚举树；另一种是通过适当编排解集中各变量分别取值0或1的各种组合的检验顺序，使之符合相应的目标函数值从小到大或从大到小的顺序，现将此类方法归纳后简述如下。

（1）对标准型要求

1）标准型。

目标函数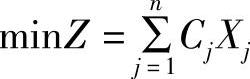

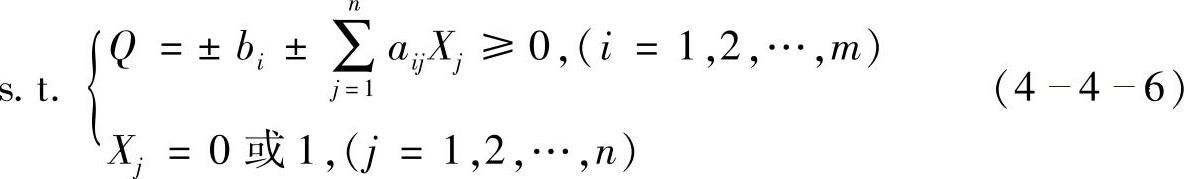
①C_j>0，（j=1，2，…，n）

②约束条件均为“>0”的形式。

③目标函数均为求极小化。

2）转化方法。

①对于C_j<0，可令X_j=1-X′_j，则X′_j，的系数为正，仅改变目标函数中常数项之值。

②对于求极大化向题，可令maxZ=-min（-Z），先求出min（-Z）之值，改变符号，即得Z值。

③对于非“≥0”形式的约束：

（A）当遇到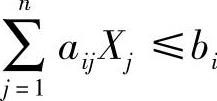形式，可变为。

（B）当遇到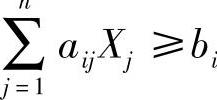形式，可变为。

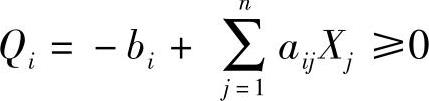（C）当遇到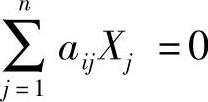形式，可变为。

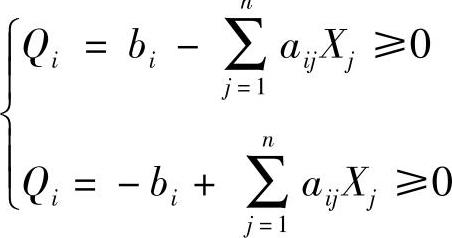（2）求解方法

从各变量取值全为0开始，通过使某个变量从0到1的转换使目标函数值从最小开始逐渐增加，并同时使解点与可行解的距离缩短而逐步过渡到可行解。在试算中用B表示与可行解的距离。

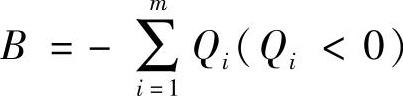
当B=0时即为可行解。因为检验的顺序是从Z值最小的解点开始并按照Z值递增的顺序，故在检验中发现的第一个可行解即为最优解。

（3）求解模型的优化算法

投资决策分析模型是一个随机01整数规划问题，模型的约束条件很有特点。如：约束条件式（4-4-3d）～式（4-4-3f）表示每一个决策阶段t中的3个随机决策变量（U^t_n，V^t_n，W^t_n）中只有一个决策变量为1，其余都为0；约束条件式（4-4-3g）～式（4-4-3j）限制所有随机决策变量组合中至多有两个1。由此可见，这些约束条件将随机决策变量组合限制在一个很有限的范围内。因此我们设计了一个优化算法来求解模型。

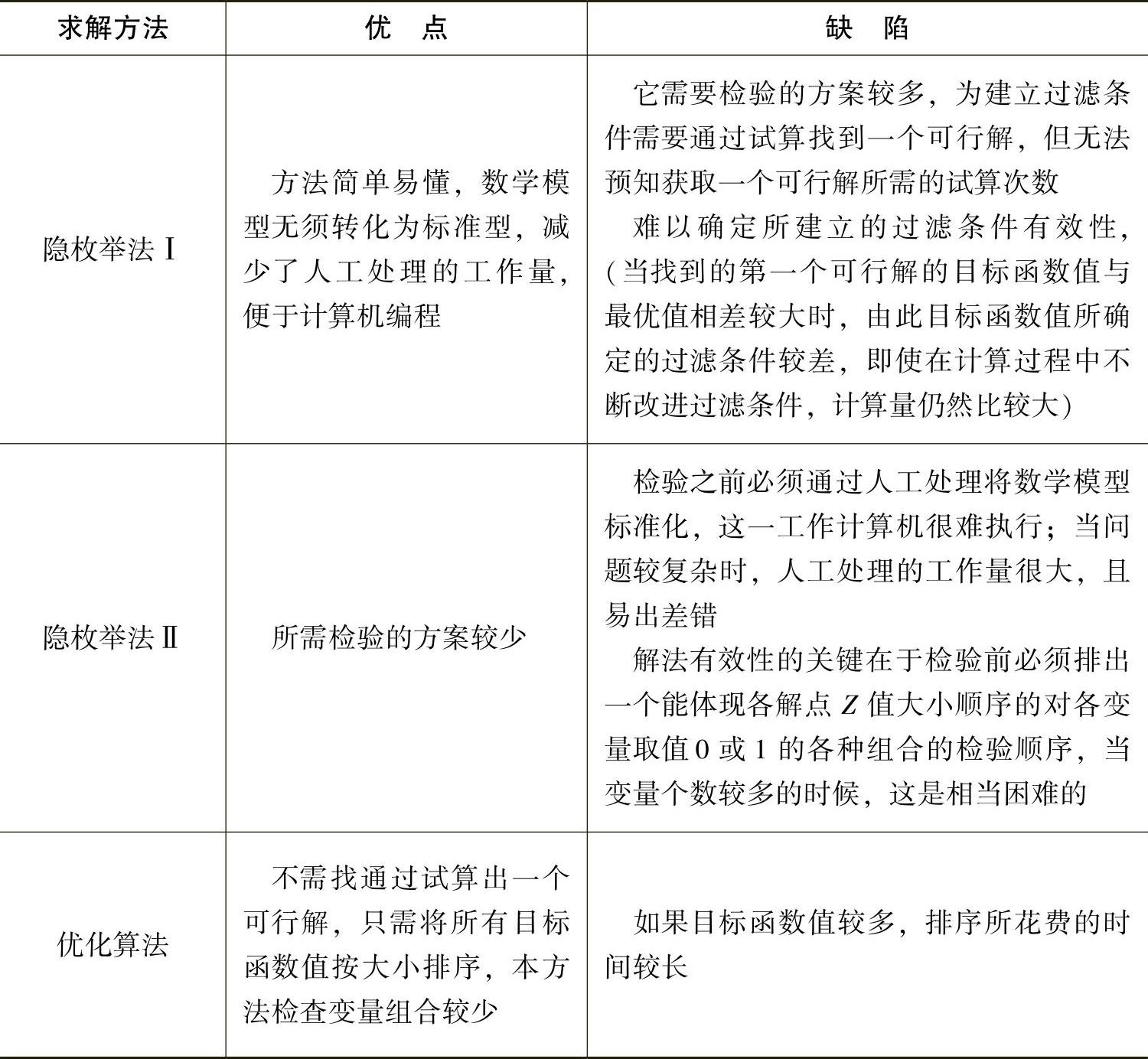
隐枚举法和优化算法的特点对照如表441所示。

表4-4-1　隐枚举法和优化算法特点对照表

（二）随机变量的离散化

Latin超立方体采样提供了一个非常有效而实用的小样本采样技术，它广泛地应用于具有随机输入变量的复杂分析模型的统计和概率分析，它给出无偏的或偏度很小的系统参数的估值，其方差较之简单的随机采样也显著减小。

Latin超立方采样方案的基本理论背景可简述如下：

设：y=f（x） （4-4-7）

代表输出变量，f（·）是一个确定性的分析模型，x=（x₁，x₂，…，x_k）T代表输入变量向量，K为输入变量数，每个输入变量x_k（k=1，2，…，K）由合适统计参数的已知分布函数F_xk（x）描述。输入变量的样本{x}_n，n=（1，2，…，N）（N是等于模拟数的样本数），按下面方式选取：

将每个输入变量x、k的已知分布F（x）、k（x）的范围分割成N个非搭接的区间S_kn，每个区间由概率P_kn表征

P_kn=P（x_k∈S_kn） （4-4-8）

且有

∑P_kn=1（k=1，2，…，k） （4-4-9）

在等概率区间的情形，有P_kn=1/N。采样时每个区间由其代表性参数代表，此代表性参数在区间中随机选取或在区间重心处选取。

随机选取时，首先在0和1间生成N个随机数，然后将它们用下式变换为区间中的随机数：

U_n=N^U+（n-1）/N （4-4-10）

式中，n=1，2，…，N，U是范围（0，1）中的一个随机数，U_n是第n个区间中的随机数。由式（4-4-10）显见，在N个区间的每一个区间中，仅有一个生成的值。

（n-1）/N<U_n<n/N（4-4-11）

式中，（n-1）/N和n/N是第n个区间的下界和上界。求得约束随机值U_n后，要求的随机变量为：

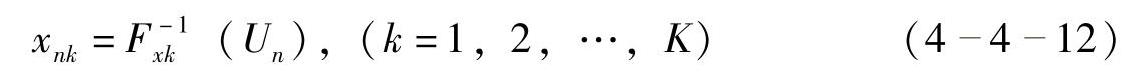
式中，F_xk^-1（·）是F_xk（·）的逆。

在区间重心处选取代表性参数时，代表性参数

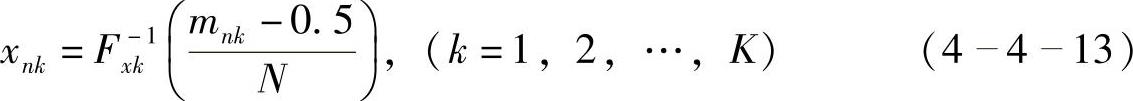
式中，m_nk是输入变量x_k用于第n个模拟的区间秩数。对于一次特殊的模拟，作为采样区间S_kn的选择是随机的，每个输入变量x_k的N个观测值与代表整数1，2，…，n的一个随机排列的整数序列（区间的序数）相联系。这些排列应是相互独立的。将它们依次放在序数随机排列的表中，表中有N行和K列，用于第n次模拟的区间序数由表中第n行表示。

（三）Benders分解法简介

Benders分解法开始是由数学家BendersJ.F在1962年提出解混合整数规划的，Benders分解解法主要是求解混合整数规划问题，亦即连续变量与整数变量同时出现的极值问题，但是它的实际应用范围广泛。这种方法把原来的大系统优化问题分解为独立的子问题求解，而一个迭代的协调过程使得子问题的解逐渐逼近原始问题的最优解。但是由于带有很大数目的约束问题，相应的极点数P和极线R是相当大的。故可采用类似Dantzig-Wolfe分解原理中应用列生成法的思想来克服这个困难。由于只有有限个极点和有限条极线，Bender算法在有限步就会收敛。

可以把这个算法看成是二级算法。低级子问题的最优对偶解只提供了原问题的X分量，而高级子问题直接提供了原问题解的Y分量。“奔德斯割”包括“可行奔德斯割”（Feasible Benders Cut）和“不可行奔德斯割”（Infeasible Benders Cut）。每一次主丛迭代中，子问题求解的情况通过主问题中的“奔德斯割”集合的变化情况反映出来：事实上，主问题中的“奔德斯割”就是由子问题的对偶解所构成的。因此，实际计算中如果子问题采用的是极小化目标函数形式，正确获取它的对偶信息将对整个算法的成功起到关键的作用。

Geoffrion1972年对下述更广泛的非线性规划提出了广义Benders分解方法，可以较有效的解决许多非线性规划问题，如果假设中的价格函数P为非线性函数。那么相应的子问题为非线性函数可以采用广义Benders分解方法求解。

（四）整个模型的求解过程

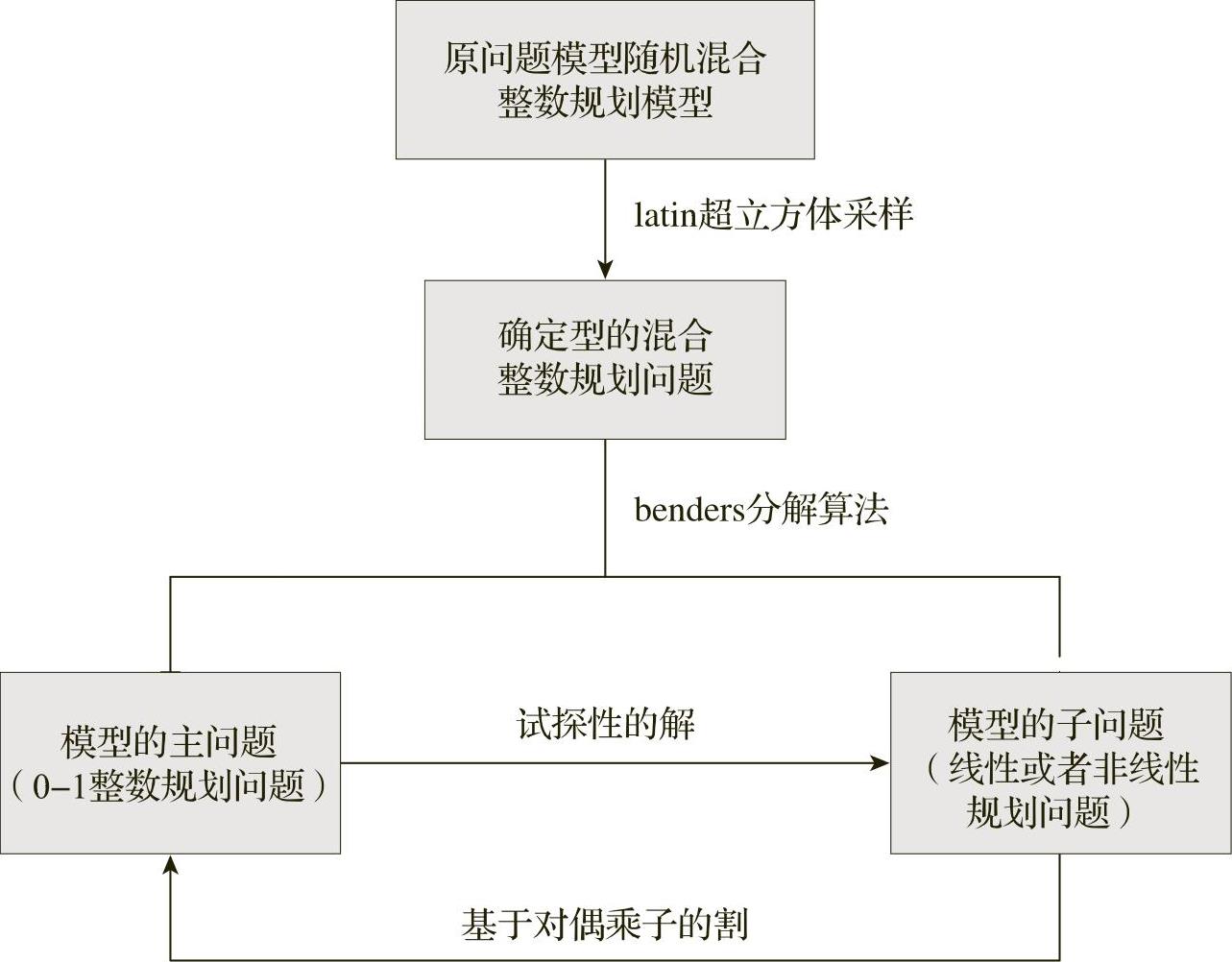
Benders分解法是求解随机混合整数规划模型的一种有效的方法。它将模型分解成主问题和子问题，主问题是一个0-1目标整数规划。它是原问题的松弛，其目标最优值是原问题目标最优值的一个下界（Lower Bound）。通过解这个目标整数规划，产生一个试探性解{U^t_r，V^t_r，W^t_r}（这个解是第r次迭代中主问题的解），传递给子问题。一旦{U^t_r，V^t_r，W^t_r}固定下来了，从而产生的子问题可以当作是一系列独立的子问题（每个子问题是针对每个时间段t的），这是因为没有约束跨越时间段了。于是，利用主问题传来的固定投资方案，就可以解选型子问题。在每轮迭代中，子问题的解产生一个或多个约束（即所谓“割”cuts），加到主问题上，进行下一轮迭代。这个过程不断持续，直到找到一个可行解，使得这个解与下界足够接近，即认为找到了最优解。这样就简化了计算量。求解过程如图444所示。

(www.daowen.com)

图4-4-4　模型整体求解过程流程图

1.初始问题转化为等价的确定型问题

采用Latin超立方体分层采样技术将原来的随机混合整数规划问题转化为等价的确定型的混合随机整数规划问题。Latin超立方体分层采样技术中所选取的S是情节树（Scenario Tree）的情节数量。由于K的对数成条件异方差高斯过程。采用Latin超立方体分层采样技术将每一个随机变量的积累分布分解成N个等概率的区间S，然后随机变量可以在每个区间内任意取值。这个值代表区间内的任何一个值。这种采样方法比蒙特卡罗模拟法采样次数要少。

具体方法如下：

第一步：将随机变量和r^t分成N个等概率的区间S，其中随机变量，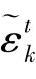

r^t都是服从N（0，1）的随机数。

第二步：从每个区间内任意选取一个值U_n，U_n=U/N+（n-1）/N，U是

范围在（0，1）中均匀分布的一个随机数。

第三步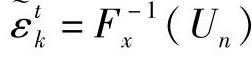：正态分布函数的反函数；

第四步：分别将随机数代入式（446）求出G^t_n，将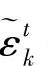代入式（44

13）求出K^t_n。

第五步：如果G^t_n≤G_min，那么令P^t_n=0，或者如果K^t_n≥K_max，那么也令

P^t_n=0

（这一步表示如果当企业产品未来的市场需求量低于G_min时，企业将暂时不投资，待企业产品需求增长后再投资ERP系统或者如果当ERP咨询培训费用超过K_max时，企业将暂时不投资，等待ERP咨询培训费下降后再投资建设ERP系统，体现出了ERP项目中存在的放弃期权和等待期权）。

原模型转化为等价的确定性的混合整数规划问题，如图445所示。

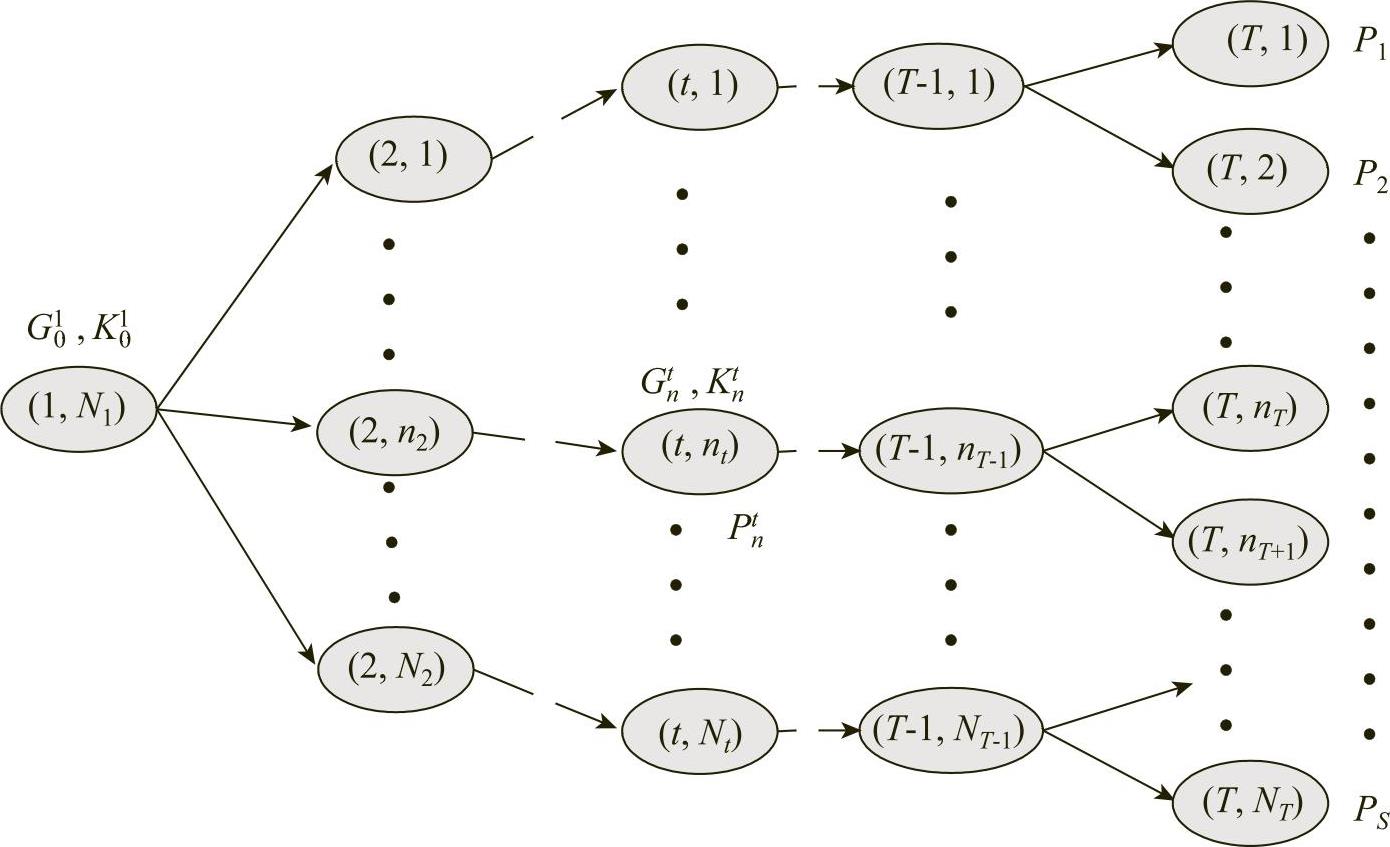
图4-4-5　情节树图

，r^t=F_x^-1（U_n），F_x^-1（·）是F_x（·）的逆，是标准

F_n^t=V_n^tL-[U_n^t（I₁^t+θ₁）+V_n^t（I_2a^t+θ_2a）+W_n^t（I_2b^t+θ_2b）]-（η₁X^t_n+η_2aY^t_n+

η_2bZ^t_n+X^t_nK^t_n+Y^t_nK^t_n）+ν₁X_n^t[V（C^t_n，t）+δV（D^t_n，t）-E]+ν₂（Y^t_n+Z^t_n）

[V（C^t_n，t）+δV（D^t_n，t）-E]

∀t∈{2，…，T}，∀n∈{1，…，N_t} （4-4-14b）

约束条件中：∀t∈{1，…，T}，∀n∈{1，…，N_t}节点（t，n）∈节点（T，n）

2.等价的确定型问题的分解和求解

用Benders分解法将等价的确定性混合随机规划模型分解成主问题和子问题。

主问题为

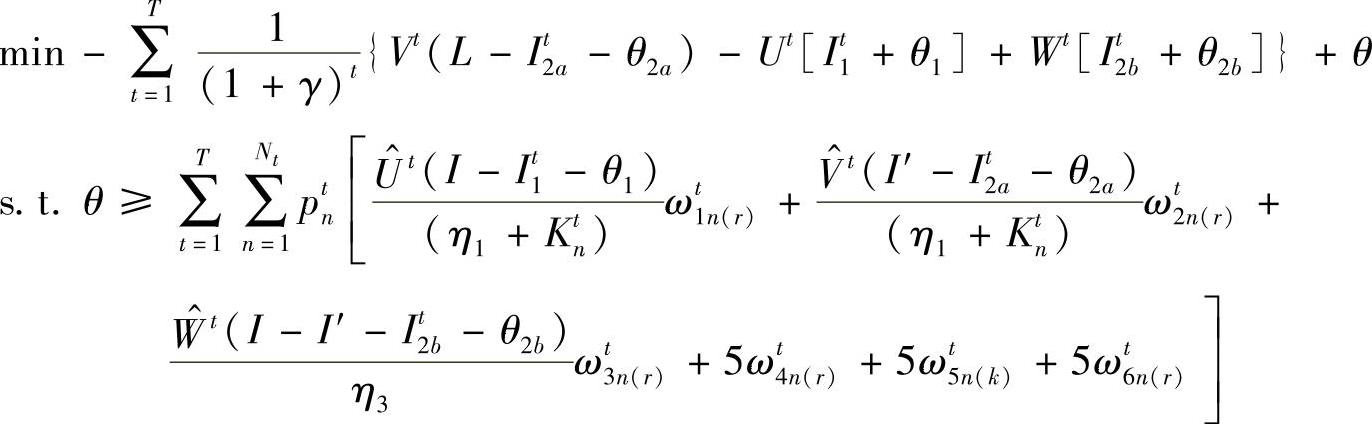
r=（1，2，…，K）

U^t，V^t，W^t∈{0，1}，∀t={1，…，4}

子问题为

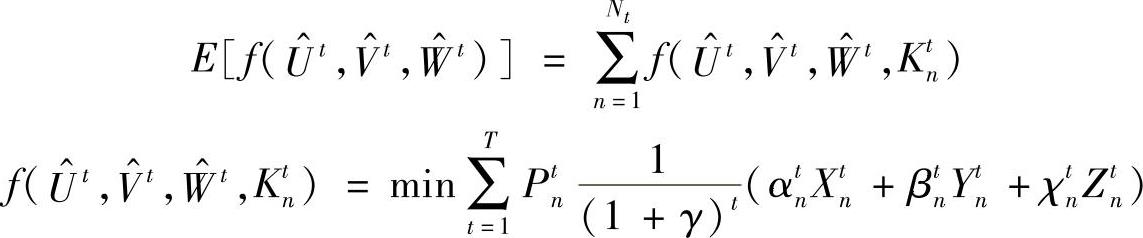
n=（1，…，N_t）

α_n^t=η₁+ν₁[V（C^t_n，t）+δV（D^t_n，t）-E]+K_n^t

β_n^t=η₂+ν₂[V（C^t_n，t）+δV（D^t_n，t）-E]+K_n^t

χ_n^t=η₃+ν₂[V（C^t_n，t）+δV（D^t_n，t）-E]

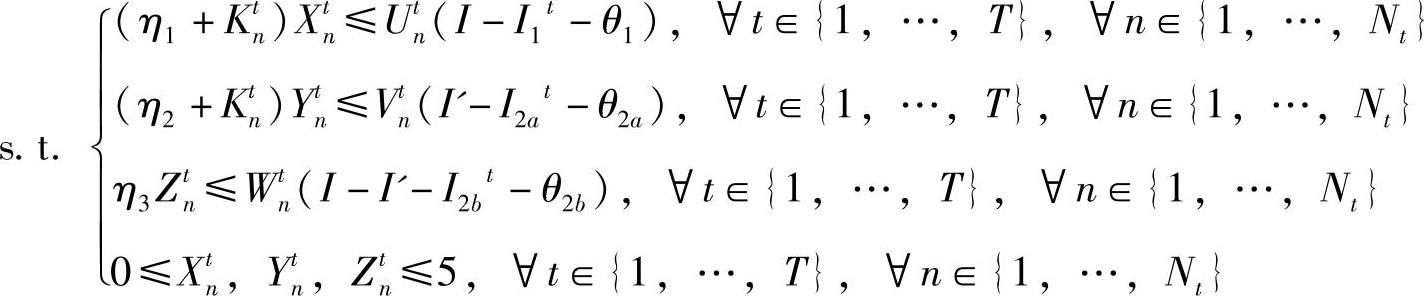
子问题的对偶问题是

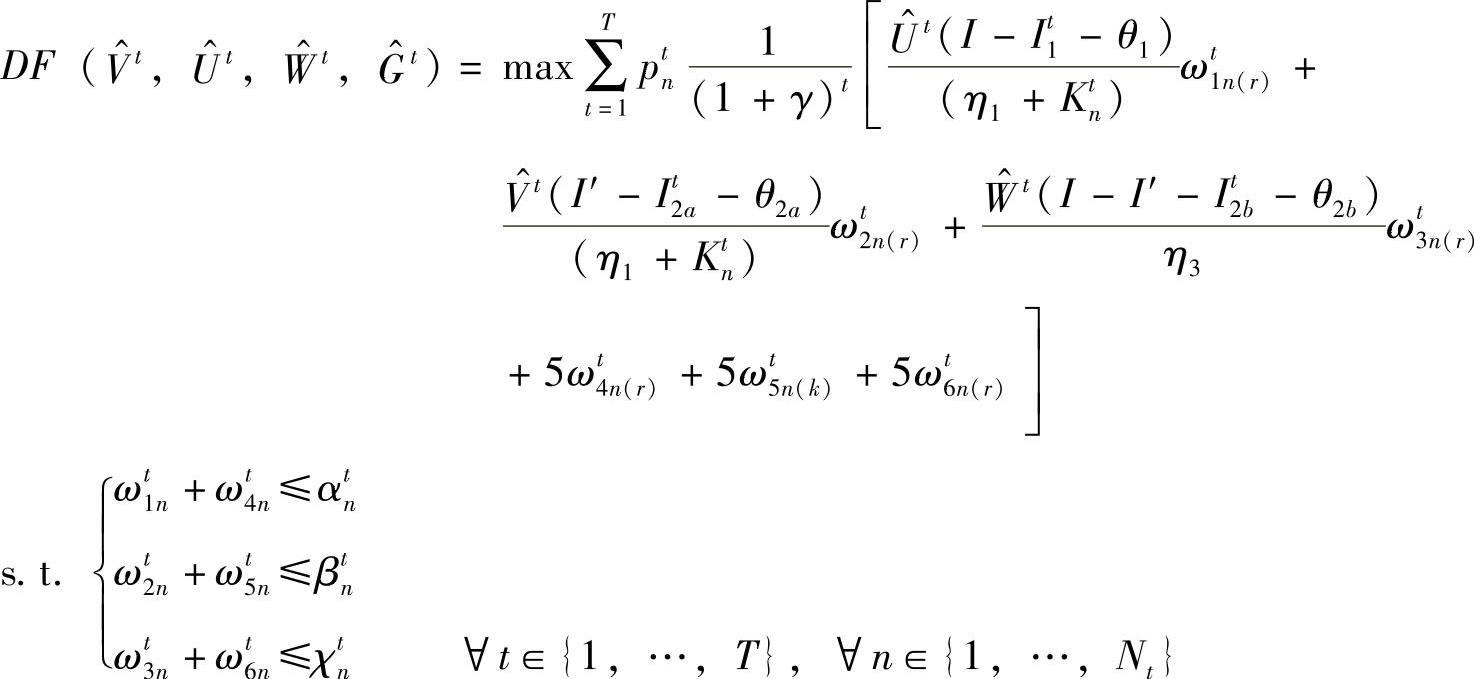
1）初始化r=0，上限+∞=UB，下限-∞=LB，取初始可行解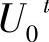，V₀^t，W₀^t。

2）对于给定的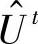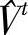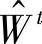，，，利用改进单纯形法和对偶理论（互补松弛性定理），求解每个样本∀t∈{1，…，T}，∀n∈{1，…，N_t}对应的子问题和对偶问题，分以下两种情况进行讨论：

①若∃n，子问题不可行，对偶问题无界，则对主问题增加约束条件。

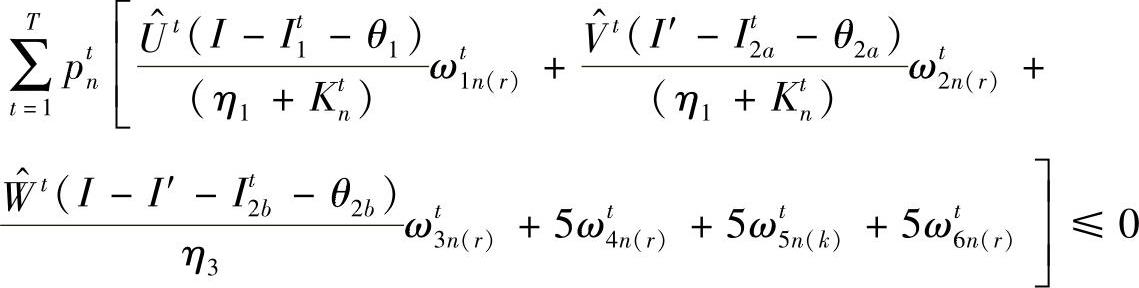
即添加割平面去掉不可行解，r=r+1，转向4；

②若m∀，子问题可行，最优解记为

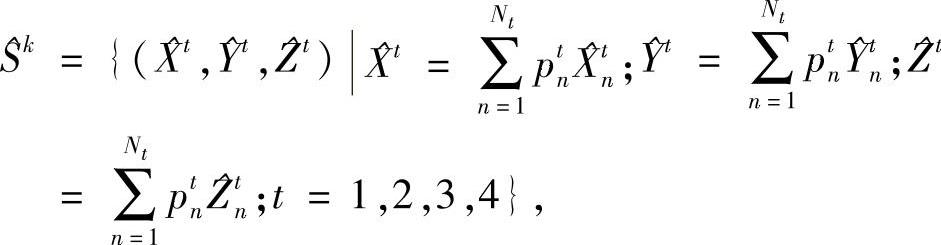
其对偶解记为：，，，，，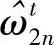

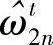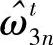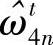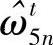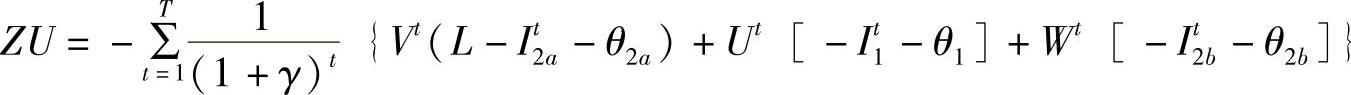
，转向3；

3）若UB-LB≤ε（ε≤0，为允许的最大差值），S∗=S^r，算法停止，否则r=r+1对主问题添加割平面

转向4；

4）利用求解整数规划的方法求解主问题，最优解为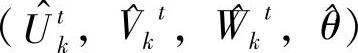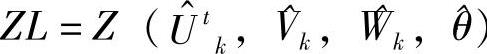，，LB=max{ZL，LB}，返回到2）。

本节在前两节分析的基础上，结合ERP系统的投资特点，基于实物期权，采用多段随机规划方法建立了一个ERP项目投资决策模型，并且设计了合理的模型求解算法。

（1）模型很好地考虑了项目投资过程中未来收益的不确定性和投入成本中咨询费用的不确定性，主要解决了如何选择投资策略、如何选择投资时机、如何选择投资规模这三个问题。

（2）模型是一个随机混合整数规划方程组，求解算法采用了Latin超立方采样技术将不确定性问题转化为定价的确定性问题，然后采用Benders分解法求解模型。算法借助计算机程序和ILOG软件包可以很快地解出模型的最优近似解，如图446所示。

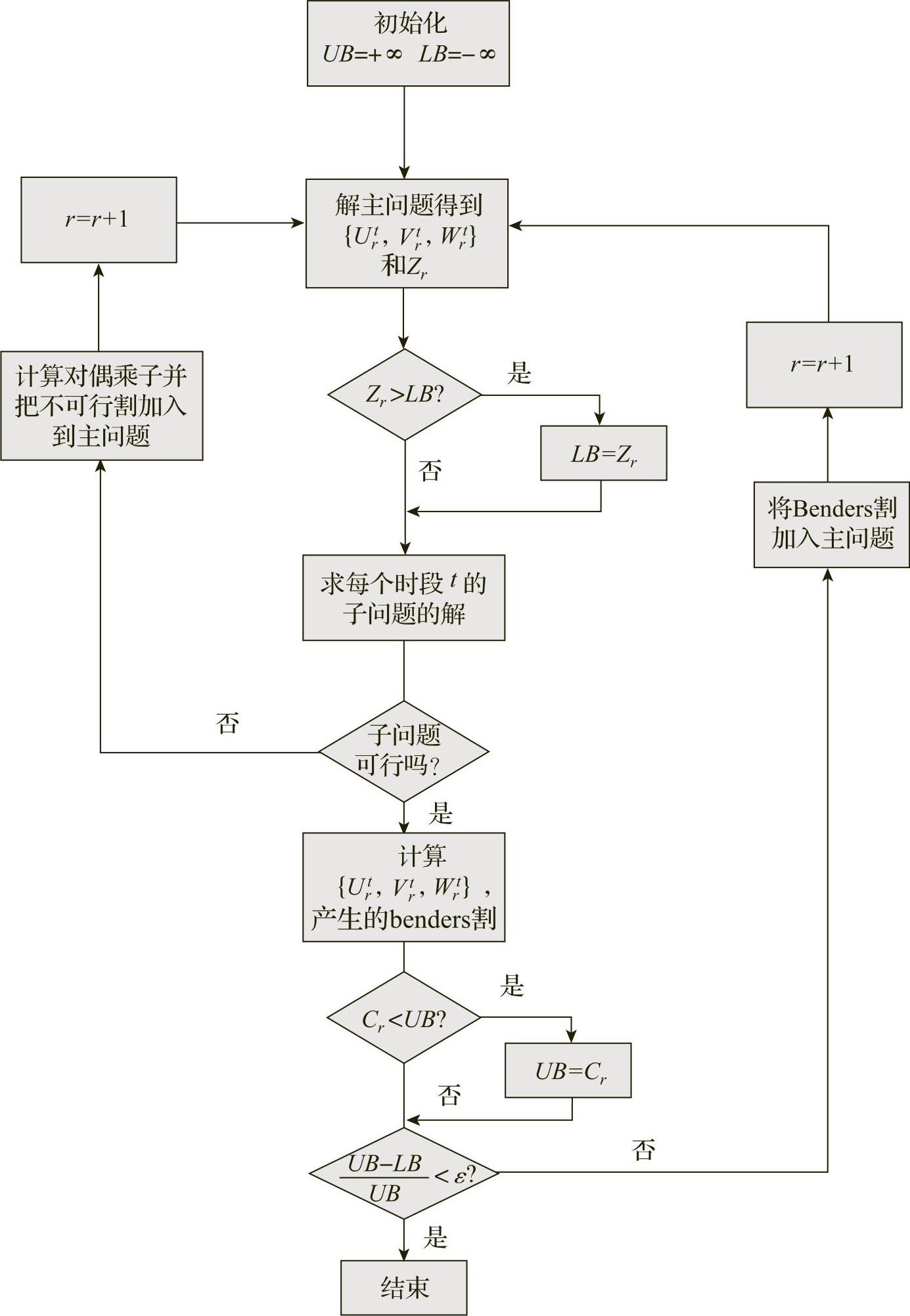
图4-4-6 Benders分解算法流程图