复合期权是写在期权上的期权，其研究起源于Black和Scholes在期权定价方面的开创性工作。他们将股票视为写在公司价值上的期权，若公司价值是写在公司债券上的期权，则股票便可表示为写在公司债券上的复合期权。复合期权可分为简单复合期权和多期复合期权。按照被复合期权的类型，简单复合期权又分为写在看涨期权上的看涨期权、写在看跌期权上的看涨期权、写在看涨期权上的看跌期权、写在看跌期权上的看跌期权，以及写在其他奇异期权上的看涨期权或者看跌期权等等。另外，按照标的资产性质的不同，复合期权还可分为金融复合期权和实物复合期权。

Geske提出了经典简单复合期权定价理论。Geske提出了可以计算以股票为标的资产的欧式看涨期权的价值，其中把作为标的资产的股票的价值看做是公司资产价值的欧式看涨期权的价值。这里暗含着早期投资机会是为后来的投资做准备时，对复合增长机会的评估。由于这里存在两个期权，且第一个期权导致第二个期权的产生，所以它是一个复合期权。且只有当第二个期权的价值大于第一个期权的执行价格时，复合期权可在第一个到期日执行期权。假设项目的价值流遵循一般的几何布朗运动，我们要借助标准的期权评价模型Black_- Scholes模型和Geske模型来建立ERP项目的复合期权评价模型

τ=t_c-t_a，τ₁=t_b-t_a，τ₂=t_c-tb

B（a，b，ρ）是积分上限为a，b，相关系数为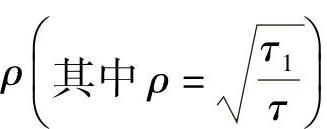的双变量累计标准正态分布函数；

式中

N（h）——单变量累计标准正态分布函数；

V——在t₂时刻进行市场推广后产生的现金流入的现值；

V³——复合期权应被执行时资产的价值V，即第二个期权价值等于第一个期权交割价格时项目的价值（由S（V³）-M₀=0解得）

σ——描述项目不确定性的波动率；(www.daowen.com)

M——进行市场推广需要的投资额；

I_b——后续研发阶段需要的投资额；

t_b——第一个期权到期的时间；

t_c——复合期权到期的时间。

V³满足下式：

其中

Geske导出的这个复合期权的定价框架为后续复合期权的研究奠定了基础。但是定价模型得到的是高维嵌套积分形式的封闭解，欲获得该解的具体数值，必须进行复杂的高维嵌套积分的计算，耗费巨大的计算资源。尤其对于多期复合期权模型，一般难以保证计算过程的收敛，不易得到问题的数值解。针对这一问题，Selby等给出了有关嵌套多维正态分布的一般恒等式，从而减少了积分的维数，提高了计算效率。Schroder^[46]对具有某种特定相关矩阵的多元积分，也提出一个换算公式，利用该公式能够显著降低高维积分的计算费用。在大多数情形下解的一般形式是难以获得的。很多学者开始采用数值方法来求解与期权有关的复杂问题，如由Cox^[47]等发展的二项式期权定价方法。Trigeorgis^[48]将二项式定价方法变形，提出一种所谓的“对数变形的二项式数值分析方法”来定价复合期权，在数值计算中可以获得很好的一致性、稳定性和有效性。Breen^[49]混合了二项式模型以及Geske和Johnson模型，提出了一种“加速二项式期权定价模型方法”，达到比传统二项式模型更快的速度，而且适用于更大范围的期权定价模型。

简单复合期权理论模型主要基于Black-Scholes框架，存在着一定的局限性。现有复合期权的理论研究主要围绕如何对简单复合期权模型进行扩展，以获得更广泛的应用。Buraschi^[50]等放松了标的资产服从几何布朗运动的假设，研究了标的资产服从一般扩散过程情形下复合期权的定价，导出了一个由欧式期权价格边界上的前向积分表达的定价公式。这样一种扩展就能够用来描述标的资产存在破产和违约的情形。在经典的复合期权理论中，波动率和利率都被假设是固定的。另一个极具有实际意义的工作是对多期复合期权模型展开研究。如（n-1）期的复合期权可视为（n-1）个前后相互关联的欧式期权C_i（i=1，…，n-1）序列。持有者在每一期的期末可以选择是否执行期权。若执行期权，则后续的一系列期权都将自动消失；如果放弃执行，则该期的期权将会延续至下一期，重复此过程直至到期日。从两期到多期的扩展在理论上并不困难，难点就在于期权价值和最优策略的计算难度和复杂性会随着期数的增加而迅速增加。大量学者在多阶段项目投资定价以及最优投资策略分析的背景下，研究多期复合期权的定价。Dixit^[51]等将多期序列投资看成是多期复合期权，分别采用动态规划方法和相机权益分析方法建立定价的偏微分方程，在一定的边界条件下求得每一期的期权价值函数以及执行临界值，通过回溯可以求得复合期权的解析解，同时得到复合期权执行的最优规则，但是缺点是只有在某些特定边界条件下才能获得解析解。Dutta^[52]采用动态规划方法来解决多阶段R&D项目在各阶段的最优资产配置问题。Alvarez^[53]等在指出传统的动态规划方法的缺陷后，基于格林函数提出一种多期复合期权通用的计算方法。这种方法能够提供更系统的方法来计算复合期权价值函数，以及刻画期权的最优执行规则。Lin^[54]则直接将简单复合期权模型的结论推广到多期的情形，给出了欧式多期复合期权解的一般形式，且对求解的各种解析近似方法进行了比较。这种方法的不足在于在解析公式的计算中仍然存在着嵌套的高维正态积分。