判异准则有点出界和界内点排列不随机两类。由于对点子的数目未加限制，故后者的模式原则上可以有很多种，但在实际中经常使用的只有具有明显物理意义的若干种。常规控制图的判断中要注意对这些模式加以识别。

国标GB/T4091—2001《常规控制图》中规定了8中判异准则。为了应用这些准则，将控制图等分为6个区域，每个区宽1σ。这6个区的标号分别为A、B、C、C、B、A。其中两个A区、B区及C区都关于中心线CL对称（参见图6-5～图6-12）。需要指明的是这些判异准则主要适用于X图和单值X图，且假定质量特性X服从正态分布。

准则1：一点落在A区以外（图6-5）。在许多应用中，准则1甚至是唯一的判异准则。准则1可对参数μ的变化及参数σ的变化给出信号，变化越大，则给出的信号越快。准则1还可对过程中的单个失控做出反应，如计算错误、测量误差、原材料不合格、设备故障等。在3σ原则下，准则1犯第一类错误的概率为α0=0.0027。

准则2：连续9点落在中心线同一侧（图6-6）。此准则是为了补充准则1而设计的，以改进控制图的灵敏度。选择9点是为了使其犯第一类错误的概率α与准则1的α0=0.0027大体相当。

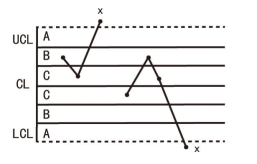
图6-5　1个点落在A区以外

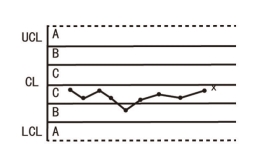
图6-6　连续9点落在中心线同一侧

出现如图6-6所示准则2的现象，主要是过程平均值μ减小的缘故。

准则3：连续6点递增或递减（图6-7）。此准则是针对过程平均值的趋势进行设计的，它判定过程平均值的较小趋势要比准则2更为灵敏。产生趋势的原因可能是工具逐渐磨损、维修逐渐变坏等，从而使得参数随着时间而变化。

准则4：连续14点相邻点上下交替（图6-8）。本准则是针对由轮流使用两台设备或由两位操作人员轮流进行操作而引起的系统效应。实际上，这就是一个数据分层不够的问题。选择14点是通过统计模拟试验而得出，也是为使其α大体与准则1的α0=0.0027相当。

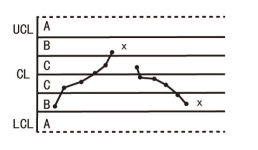
图6-7　连续6点递增或递减

(www.daowen.com)

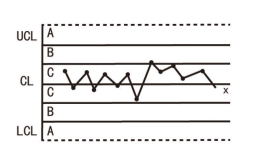
图6-8　连续14点中相邻点交替上下

准则5：连续3点中有2点落在中心线同一侧的B区以外（图6-9）。过程平均值的变化通常可由本准则判定，它对于变异的增加也比较灵敏。这里需要说明的是：三点中的两点可以是任何两点，至于第三点可以在任何处，甚至根本不存在。出现准则5的现象是由于过程的参数μ发生了变化。

准则6：连续5点中有4点落在中心线同一侧C区以外（图6-10）。与准则5类似，这第5点可在任何处。本准则对于过程平均值的偏移也是比较灵敏的，出现本准则的现象也是由于参数μ发生了变化。

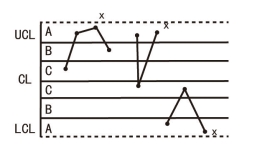
图6-9　连续3点中有2点落在中心 线同一侧的B区以外

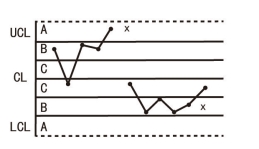
图6-10　连续5点中有4点落在中心线同一侧的C区以外

准则7：连续15点在C区中心线上下（图6-11）。出现本准则的现象是由于参数σ变小。对于这种现象不要被它的良好“外貌”所迷惑，而应该注意到它的非随机性。造成这种现象的原因可能有数据虚假或数据分层不够等。在排除了上述两种可能性之后才能总结现场减少标准差σ的先进经验。

准则8：连续8点在中心线两侧，但无一在C区中（图6-12）。造成这种现象的主要原因也是因为数据分层不够，本准则即为此而设计的。

图6-11　连续15点落在中心线两侧的C区内

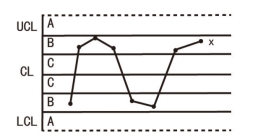
图6-12　连续8点落在中心线两侧且无一在C区内