（一）控制图的形成

将通常的正态分布图转个方向，使自变量增加的方向垂直向上，将μ、μ+3σ和u-3σ分别标为CL、UCL、LCL，这样就得到了一张控制图。如图6-3所示，是一张单值（X）控制图，图中的UCL为上控制限，CL为中心线，LCL为下控制限。

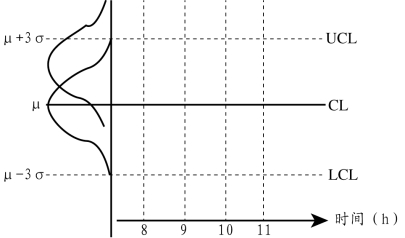
图6-3　SPC控制图-X控制图

（二）控制图原理的第一种解释

为了控制加工螺丝的质量，每隔1小时随机抽取一个加工好的螺丝，测量其直径，将结果描点在图6-3中，并用直线段将点子连接。以便观察点子的变化趋势。由图6-3可看出，前3个点子都在控制界限内，但第4个点子却超出了UCL，为了醒目，把它用小圆圈圈起来，表示第4个螺丝的直径过分粗了，应引起注意。现在对出现的这第4个点子应做什么判断呢？摆在我们面前的有两种可能性。

（1）若过程正常，即分布不变，则出现这种点子超过UCL情况的概率只有1‰左右。

（2）若过程异常，譬如设异常原因为车刀磨损，则随着车刀的磨损，加工的螺丝将逐渐变粗，u逐渐增大，于是分布曲线上移，发生这种情况的可能性很大，其概率可能为1‰的几十乃至几百倍。(www.daowen.com)

现在第4个点子已经超出UCL，问在上述的（1）（2）两种情形中，应该判断是哪种情形造成的？由于情形（2）发生的可能性要比情形（1）大几十乃至几百倍，所以合乎逻辑的认为上述异常是由情形（2）造成的。于是得出结论：点出界就判异。

用数学语言来说，这就是小概率事件原理：小概率事件在一次试验中几乎不可能发生，若发生即判断异常。控制图是假设检验的一种图上作业，在控制图上每描一个点就是一次假设检验。

（三）控制图原理的第二种解释

现在换个角度来研究一下控制图原理。根据来源的不同，影响质量的原因（因素）可归结为5M1E（人员、设备、原材料、工艺方法、测量和环境）。但从对产品质量的影响大小来分，又可分为偶然因素（简称偶因）与异常因素（简称异因，在国际标准和我国国家标准中称为可查明原因）两类。偶因是过程固有的，始终存在，对质量的影响微小，但难以除去，例如机床开动时的轻微震动等。异因则非过程固有，有时存在，有时不存在，对质量影响大，但不难除去，例如车刀磨损等。

偶因引起质量的偶然波动，异因引起质量的异常波动。偶然波动是不可避免的，但对质量影响一般不大。异常波动对质量的影响大，且可以通过采取恰当的措施加以消除，故在过程中异常波动及造成异常波动的异因是我们注意的对象。一旦发生异常波动，就应该尽快找出原因，采取措施加以消除。将质量波动区分为偶然波动和异常波动两类并分别采取不同的对待策略，这是休哈特的研究成果。

偶然波动与异常波动都是产品质量的波动，如何能发现异常波动的存在呢？我们可以这样设想：假定在过程中，异常波动已经消除，只剩下偶然波动，这当然是正常波动。根据正常波动，应用统计学原理设计出控制图相应的控制界限，当异常波动发生时，点子就会落在界外。因此点子频频出界就表明存在异常波动。控制图上的控制界限就是区分偶然波动和异常波动的科学界限。

根据上述，可以说休哈特控制图即常规控制图的实质是区分偶然因素与异常因素的两类因素。