（一）找出所有测量不确定度的来源

根据测量原理和对测量过程的了解，列出对测量结果有明显影响的所有测量不确定度来源（即影响量），并要做到不遗漏和不重复。如果所给出的测量结果是经过修正后的结果，应当考虑由修正值（或修正因子）所引入的不确定度分量。

（二）写出数学模型

数学模型是指被测量Y与各影响量Xi之间的具体函数关系，若被测量Y的测量结果为y，影响量Xi估计值为xi，则数学模型的一般形式可以写为

Y=f（x1，x2，…，xn）

数学模型中应包括所有对测量结果及其不确定度有影响的影响量。此后不确定度评定中所考虑的不确定度分量应与数学模型中的影响量一一对应。

（三）输入量估计值x的标准不确定度u（x）

1.测量不确度的A类评定

输入量估计值x由实验测量得到，则有可能采用A类评定来得到其标准不确定度u（x）。

（1）单次测量结果xk的标准不确定度u（xk）

若在重复性条件下对影响量X作n次独立重复测量，得到测量结果为xk（k=1，2，…，n），则n次测量结果的平均值为

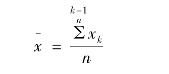
单次测量结果xk的标准不确定度u（xk）为

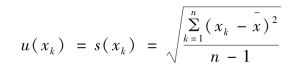
（2）N次测量结果平均值的标准不确定u（x-）度：

若所给的测量结果是N次测量结果的平均值，且N可以不等于n，则N次测量平均值的标准不确定度u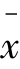（）为

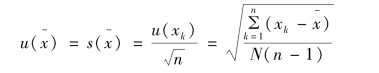
（3）合并样本标准偏差sp（xk）

如果可能，输入量的标准不确定度u（xk）也可以用合并样本标准差sp（xk）得到，其表示式为

式中 m——测量的组数；

n——每组包含的测量次数；

xkj——第j组中第k次的测量结果；

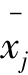——第j组测量结果的平均值。

2.测量不确定度的B类评定

若输入量估计值x由其他各种信息来源得到，则只能采用B类评定来得到其标准不确定度u（x）。

（1）若已知输入量估计值x的扩展不确定度U（x）和包含因子k，则x的标准不确定度为

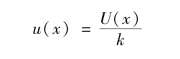
（2）若已知输入量估计值x的扩展不确定度Up（x），此时置信概率p为已知，则其包含因子k将与x的分布有关，此时除非另有说明，一般可按正态分布考虑。正态分布时对应于不同置信概率p的包含因子kp的数值见下表4-1。

表4-1　正态分布时的包含因子

（2）若已知输入量估计值x可能值的分布区间半宽度a（通常为允许误差的绝对值），则x的标准不确定度为

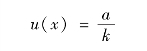
此时包含因子k将与x的分布有关。在各种情况下影响量x分布的判定原则参见JJF1059-1999。常见分布包含因子k的数值见表4-2。

表4-2　常见分布的包含因子k

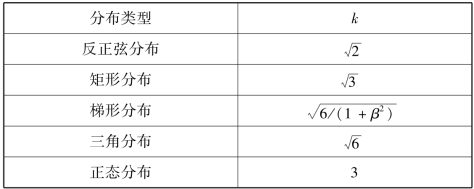
注：β为梯形分布的角参数，等于梯形的上、下底宽度之比。

（四）不确定度分量ui（y）

根据各输入量的标准不确定度u（xi），并通过由数学模型得到的灵敏系数ci，可得到对应于输入量xi的不确定度分量ui（y），即

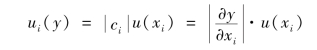
原则上，如果无法得到输入量xi与被测量y之间的函数关系，那么灵敏系数ci也可以由实验测量得到。(www.daowen.com)

（五）合成标准不确定度uc（y）

（1）如果数学模型为线性模型，即被测量y可以表示为

y=y0+c1x1+c22+…+cnxn

那么成标准不确定度uc（y）为

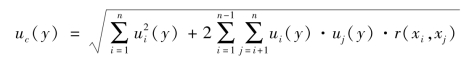
式中 r（xi，xj）——输入量xi和xj之间的相关系数。

若各输入量之间均不相关，或虽存在相关的输入量，但其相关系数较小而可以忽略，此时合成标准不确定度uc（y）可简化为

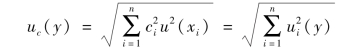
（2）若数学模型为连乘或连除的模型，即被测量y可以表示为

在可以不考虑指数pi的不确定度的情况下，合成相对标准不确定度ucrel（y）可表示为

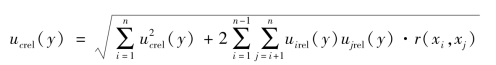
若各输入量之间均不相关，或虽存在相关的输入量，但其相关系数较小而可以忽略，于是合成相对标准不确定度ucrel（y）可简化为

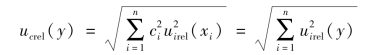
在此情况下，合成相对标准不确定度的表示形式与标准的线性模型完全相同，其差别仅是应将原来表示式中所有的不确定度全部改为相对不确定度，也就是是说此时所有各不确定度分量应该用相对不确定度来表示，（绝对）不确定度u（y）和相对不确定度urel（x）之间的关系为

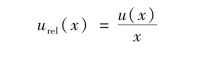
（六）扩展不确定度及其表述

扩展不确定度等于合成标准不确定度与包含因子k或kp的乘积，而包含因子的数值取决于被测量y分布，因此在得到合成标准不确定度uc后，需对被测量y的分布进行估计。

1.被测量分布的估计

（1）可以估计被测量接近于正态分布；

（2）可以估计被测量接近于某种非正态分布，例如矩形分布、三角分布、梯形分布等；

（3）无法判断被测量的分布。

对应于不同的被测量y的分布，应采用不同的方法得到包含因子。

2.不同分布时的包含因子以及扩展不确定度的表述

（1）若可以估计被测量接近于正态分布，则可采用下述两种方法之一得到包含因子k：

①估算出对应于各不确定度分量和自由度νi及对应于合成标准不确定度uc（y）的有效自由度νeff，最后根据规定的置信概率p和有效自由度νeff由t分布得到kp值，此时扩展不确定度应该用Up的形式表示，即

U95=k95·uc=t95（νeff）·uc或U99=k99·uc=t99（νeff）·uc

在最后的不确定度陈述中应给出Up（具体地说U95或U99），νeff，最好同时给出包含因子kp。

②在正态分布的情况下，若可以估计有效自由度νeff不太小，例如不小于15，则可以简单取包含因子k=2，昆时扩展不确定度用U表示，即

U=2uc

在此情况下，在对不确定度进行最后陈述时，除了应给出U和k之外，还可以进一步指出：由于估计被测量接近于正态分布，且其有效自由度不太小，所以对应的置信概率约为95%。

（2）若可以判断被测量y接管于某种已知的非正态分布，例如，矩形分布、三角分布或梯形分布等，则包含因子kp的数值可以由规定的置信概率p计算得到。三种分机上的k95和k99的数值见表4-2。

被测量接近于矩形分布、三角分布和梯形分布时的包含因子。

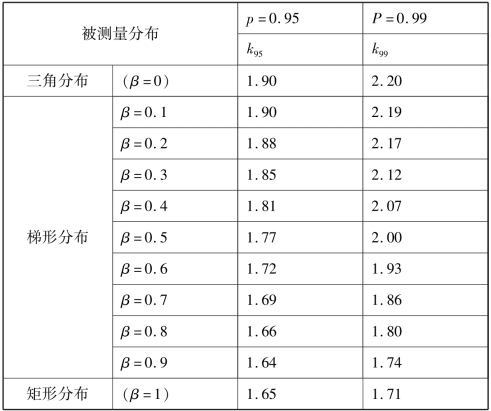
注：（1）梯形分布的k值与其角参数值β有关。
（2）当β=0，梯形分布成为三角分布；当β=1，梯形分布成为矩形分布。

在此情况下，由于包含因子是由规定的置信概率p和估计的被测量分布得到，所以扩展不确定度应该用Up的形式表示，即

U95=k95·uc或U99=k99·uc

最后的不确定度陈述中应给出Up（具体地说是U95或U99），包含因子kp，以及被测量y的分布。

（3）当无法判断被测量y的分布时，或某领域有规定时，可直接取包含因子k=2，此时扩展不确定度用U表示，即

U=2uc

最后的不确定度陈述中应给出U，以及k=2。