风险分析的常用工具和方法有概率分布方法和盈亏平衡分析方法等，现就概率分布方法作简要介绍。

（一）概率分布

对于同一个事件在不同条件下所形成的概率变化状况是用概率分布来描述的。当反映同一个事件变化的随机变量仅可能是有限个或可列无限个时，表现它的概率变化状况的是离散型概率分布，如二项分布、泊松分布等；而当反映同一个事件变化的随机变量是连续无限时，表现它的概率变化状况的是连续型概率分布，如正态分布、指数分布等。

1.二项分布

二项分布属离散型概率分布（见图1-2），表示当对事件A进行n次独立试验，每次A出现的概率是P时，事件A能有ξ次成功的概率。其通式为

式中 ξ——随机变量，可以取0，1，2，…，n。

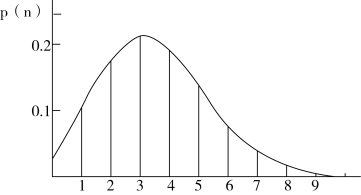
图1-2　二项分布示意图

2.泊松分布

泊松分布也属离散型概率分布，表示随机变量ξ取0，1，2，…等值时，概率分布相应的概率为

泊松分布常用来描述和解决稀有事件的概率问题，如电话交换台呼唤次数，车站等候人数、织机在一段时间内的断头数等。

3.正态分布(www.daowen.com)

正态分布属连续型概率分布，是二项分布的极限情况（n连续且趋于无穷大），其分布曲线呈钟形对称，如图1-3所示。

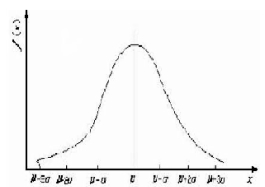
图1-3　正态分布示意图

正态分布的概率分布密度函数为

式中 μ——正态分布的期望值；

σ——正态分布的标准差。

如果μ=0即为标准正态分布，其图形以纵轴为对称轴。

经验证实在经济活动中，许多事件的概率要么服从正态分布，要么经适当变形渐近地服从正态分布。其主要参数的经济学含义是，期望值μ代表收益率的期望值，标准差σ代表风险的大小。

（二）概率分布的风险意义

1.用概率分布的分散程度说明风险的大小

概率分布越分散，风险越大，也就是说，标准差σ越大，风险越大；反之，风险越小，这是因为概率分布越分散，表明实际结果远离期望值的概率就越大，而概率分布越密集，实际结果远离期望值的概率就越小。

2.用概率分布的标准差与期望值之比来比较风险的大小

通常把概率分布的标准差与期望值的比σi/μi险度（也称方差系数），用Fdi表示。风险度Fdi越大，表示风险越大。