半变异函数（又称半变差函数或半变异矩），是地统计分析的特有函数，是描述区域化变量随机性和结构性特有的基本手段。表征半变异函数特点的五个重要参数分别是块金值（Nugget）、基台值（Sill）、偏基台值（Partial Sill）、变程（Range）和曲率（Curvature），它们之间的关系如图6－1和图6－2所示。将两个采样点之间距离非常接近时的半变异函数值定义为块金值，又被称为基底效应，它是由测量误差和空间分异的一方或两者共同作用产生的，它的值越大表明样本间的分异程度越大且样本间的分异更多是由随机性因素引起的，反之则表明样本间的分异程度越小且样本间的分异更多是由非随机性因素引起的。当采样点间的距离增大时，半变异函数值从初始的块金值逐渐增大到一个相对稳定的常数，这个常数被称为基台值，当半变异函数值超过基台值时，函数值不随采样点间隔距离而改变，从而区域变量的空间相关性不存在。基台值越大则空间分异现象越明显，基台值越小则空间越呈均衡分布状态。将基台值和块金值的差值定义为偏基台值，它的值越大则表明样本间的分异程度越大且样本间的分异更多是由结构性因素引起的，反之则表明样本间的分异程度越小且样本间的分异更多是由非结构性因素引起的。将半变异函数值取值为基台值时采样点间隔距离称为变程，它表示了在某种观测尺度下区域变量空间相关性的最大作用范围，其大小受到观测尺度的限制。它的值越大则表明区域变量空间相关性的作用范围越大，它的值越小则表明区域变量空间相关性的作用范围越小。如果各个方向上的变程相同或相近，则区域化变量为各向同性；如果各个方向上的变程相差较大，则区域化变量为各向异性，且数值大的方向上空间分异较大。

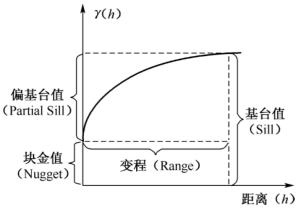
图6－1　半变异函数

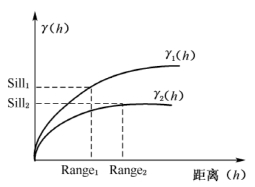
6－2　半变异函数的各向异性曲线

半变异函数的曲率指的是半变异函数和间隔距离之间关系的双对数直线回归方程中的斜率。它的值越接近于2，区域化变量之间的空间自相关强度越弱，其空间分布越均衡；它的值越远离2，区域化变量之间的空间自相关强度越强，其空间分异现象越明显。(www.daowen.com)

半变异函数的公式可以表示为：

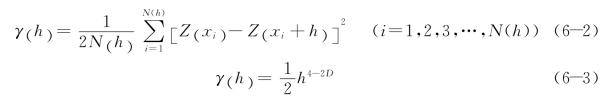
式中，γ（h）为半变异函数值；xi为第i个样本点的空间位置；h为间隔距离；Z（xi）为区域变量Z（x）在空间位置xi上的观测值；N（h）为间隔距离为h时的样本点总对数；D为半变异函数的曲率。

理论上半变异函数γ（h）是未知的，它的值可以通过从有效的空间取样数据中针对各种不同的h值计算出的一系列γ（h）进行拟合，常用的拟合模型有球状模型、高斯模型、指数模型、幂函数模型、线性模型和抛物线模型等。

本书运用半变异函数分析区域经济空间极化态势、幅度、成因、方向性等演变特征，以便更清楚地认知区域经济空间极化的格局、过程，总结出其规律，为区域经济空间协调发展指引方向。