5．3．1．1　时间序列的加法模型

对于一个时间序列，可采用加法模型来进行描述，即：

Yt＝Tt＋St＋Ct＋It　（5－4）

式中，Yt表示某一个时间序列；Tt表示这个时间序列的长期发展趋势及潜在水平；St表示这个时间序列受季节变动影响的一年一度的周期性演化，是描述周期长度小于1年的周期波动；Ct则表示这个时间序列围绕长期发展趋势Tt上的周期演化波动，主要是周期长度大于1年的周期波动；随机因子It是各种偶然因素造成的随机扰动。

本书研究的时间序列是刻画以年为最小单位的演化规律，季节波动不在研究范围，而随机扰动的大量偶然因素对区域差异演化的影响很小，可以忽略不计，因此，所研究的时间序列演变过程中的本质性规律是长期发展趋势和短期周期波动的规律。

5．3．1．2　HP滤波法

HP滤波法是霍椎克和普雷斯克特（Hodrick and Prescott，1980，1997）通过采用对称的数据移动平均方法原理设计的一个滤波器（HP滤波器）将长期趋势和短期周期波动从一组演化的时序数据中相分离的一种滤波方法，最初是应用于经济周期的研究中，后被西方学者广泛地应用于宏观经济数据的平稳性研究中。

假设某项社会经济活动运行由两部分组成，一部分由长期因素决定，另一部分由短期因素决定，则该项社会经济活动运行可以被表示为：，其中Yt表示第t期该项社会经济活动运行实际状况，和分别表示由长期因素和短期因素决定的第t期的该项社会经济活动运行的潜在趋势和短期周期波动。根据HP法，可以通过以下规划生成：

式中，n表示样本的数量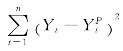；是对短期波动部分的度量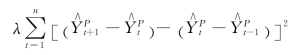；是对趋势部分“平滑程度”的度量；λ为平滑参数。

求解这一规划可得到一阶条件和边界条件如下：

用Y和分别表示由Y1，Y2，…，Yn和组成的向量，用A表示的系数矩阵，即有

利用SAS／IML／EVIEWS软件可解得，则短期周期波动数据由下式生成：

HP滤波法的一个关键问题就是平滑参数λ的取值，不同的λ值决定不同的滤波器，短期波动的周期方式和长期趋势的平滑度也不同。λ值越大，长期趋势部分的演化在规划中的权重越高，其路径就越平滑，而短期波动也就越剧烈，反之则长期趋势部分的演化路径越陡峭而短期波动越平缓。目前在处理月度和季度数据方面，λ值分别沿用Hodrick和Prescott（1980，1997）所设置的14 400和1 600，这一点经济学家基本达成共识。但是，在处理年度数据时的λ取值，经济学家的分歧较大：Backus和Kehoe（1992）认为λ应取值100；Correia、Neves和Rebelo（1992）及Cooley和ohanian（1991）认为λ应取值400；Baxter和King（1999）的研究表明λ应取值10；通过在频域上比较HP滤波转移方程的图像、分析HP滤波的转移方程以及进行蒙特卡罗实验，Ravn和Uhlig（2002）认为λ应取值为观测数据频率的4次方，即λ取值为6．25。本书在进行时间序列数据的长期趋势和短期波动分离时λ取值全部为6．25。

本书运用HP滤波法将区域经济空间极化程度的演变过程分离为长期趋势和短期波动，分别对这二者进行特征分析，在此基础上总结出区域经济空间极化程度的演变规律。

5．3．1．3　时间序列拐点(www.daowen.com)

时间序列拐点是时间序列从一个模式到另一个模式的转变点，在社会经济活动研究领域中多被用来描述某种情形持续上升一段时间后开始回落或持续下降一段时间后开始回升的现象。这种点不是数学上的拐点，而是极值点或驻点。时间序列拐点可以将时间序列划分为具有不同模式的阶段，研究者可以通过对其分析从而充分地了解时间序列的演变过程和演变规律。

假设有一个时间序列函数Y＝f（t），定义域为（0，δ］，且在点t0i的邻域U（t0i，θ）内具有一阶导数和二阶导数，其中δ为正数，θ为实数，则极值点的求解步骤如下：

首先，求函数的一阶导数f′（t），并令f′（t）＝0，求得驻点t0i。

其次，求函数的二阶导数f″（t），并将t0i代入其中，若f″（t0i）＜0，则f（t0i）是极大值，也就是由增大转变为减小的拐点；若f″（t0i）＞0，则f （t0i）是极小值，也就是由减小转变为增大的拐点。

本书利用时间序列拐点分析区域经济空间极化程度的演变过程，在此基础上总结区域经济空间极化程度的整体演变规律和阶段性演变规律。

5．3．1．4　自回归移动平均模型（ARMA模型）

自回归移动平均（Autoregressive Moving average，简称ARMA）模型是由美国统计学家George Edward Pelham Box和英国的统计学家Gwilym Meirion Jenkins在20世纪70年代提出的时间序列分析模型，是一类常用的随机时序模型，是一种精度较高的短期预测方法。它不需要事先假定数据存在着一定的结构，而是从数据本身出发去寻找可以较好描述数据的模式以保证模型与数据较好的拟合。ARMA模型在理论上已趋于成熟，且其操作简便、预测精度较高，从而被广泛应用于自然、社会和经济等众多领域。一般的ARMA（p，q）模型数学表达式为：

φp（B）＝1－φ1B－φ2B2－…－φpBp　（5－11）

θq（B）＝1－θ1B－θ2B2－…－θqBq　（5－12）

式中，是一个稳定的时间序列；αt是一个白噪声序列；B为后移算子；p为AR的阶数；q为MA的阶数。当p＝0时，ARMA（p，q）＝ARMA（0，q）＝MA（q）；当q＝0时，ARMA（p，q）＝ARMA（p，0）＝AR（p）。

如果某一时间序列是非平稳序列，则需要经过差分处理后产生一个平稳的新序列，然后才可以用ARMA模型去模拟，模拟这类序列的模型称为自回归求和移动平均（Autoregressive Integrated Moving Average，简称ARIMA）模型，其表达式为：

φp（B）（1－B）dYt＝θ0＋θq（B）αt　（5－13）

式中，d为差分阶数；θ0为确定性趋势项。

本书运用自回归移动平均模型对区域经济空间极化程度的演变过程进行模拟，以分析其演变规律。