确定型决策问题的特点是：决策问题所处的状态是明确的，每个方案只有一种确定的结果。决策者的任务是从被选方案中选择一个满意的方案。确定型决策问题看起来非常简单，但实际涉及的问题还是比较复杂的。由于确定型决策问题面临的自然状态表现为不变的外部条件，因而选择方案往往表现为某种优化问题，故对这类问题的决策多使用规划方法，包括线性规划、动态规划等。在这里我们重点给大家介绍量本利分析方法。

量本利分析法是根据产量、成本、利润三者之间的相互关系，进行综合分析，预测利润，控制成本的一种数学分析方法，通常也称为“盈亏分析法”。利用量本利分析法可以计算出组织的盈亏平衡点，又称保本点、盈亏临界点、损益分歧点、收益转折点等。

量本利分析法由美国的沃尔特·劳漆斯特劳赫在20世纪30年代首创。其基本原理是：当产量增加时，销售收入成正比增加；但固定成本不增加，只是变动成本随产量的增加而增加，因此，企业的总成本的增长速度低于销售收入的增长速度，当销售收入和总成本相等时（销售收入线与总成本线的交点），企业不盈也不亏，这时的产量称为盈亏平衡点产量，如图3.1所示。

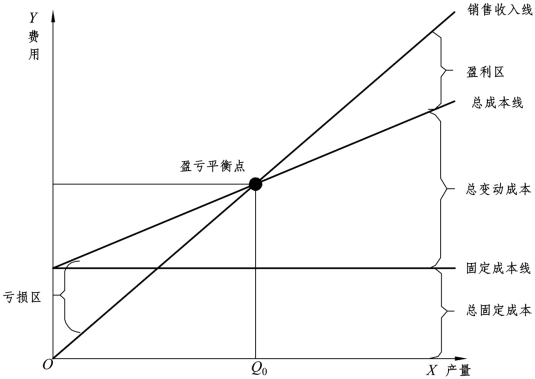
图3.1　量本利分析法

进行量本利分析的关键是确定盈亏平衡点，也就是说在盈亏平衡点上的利润为零，这时销售收入等于总成本，则盈亏平衡模型为：

销售收入＝总成本

在此基础上，如果组织期望获得利润，那么，销售收入一定要大于总成本，也就是说销售收入减总成本等于利润，则盈利模型（即量本利模型）为：

销售收入－总成本＝利润

由于总成本包括固定成本和变动成本，则量本利模型变为：

销售收入－固定成本－变动成本＝利润

也就是：

销售收入＝固定成本＋变动成本＋利润

如果用销售量乘以单价来代替销售收入，用销售量乘以单位变动成本来代替变动成本，则量本利模型变为：

销售量×单价＝固定成本＋销售量×单位变动成本＋利润

为了使用简便，该模型可以用代数式表示：

QP＝F＋QV＋M

式中：Q——销售量；

P——单位产品价格；

F——固定成本；

V——单位变动成本；

M——利润；

QP——销售收入；

QV——变动成本。

上述模型就是量本利基本模型，如果按贡献毛益考虑，上式中：

F＋M＝贡献毛益

P－V＝单位贡献毛益

（P－V）/P＝贡献毛益率

综上所述，可将量本利模型归纳如下：

1.等式法

盈亏平衡点（保本）的销售收入模型：

QP＝F＋QV(www.daowen.com)

有期望利润的销售收入模型：

QP＝F＋QV＋M

盈亏平衡点（保本）的销售量模型：

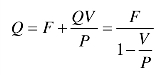
有期望利润的销售量模型：

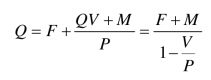
2.贡献毛益法

盈亏平衡点（保本）的销售收入模型：

有期望利润的销售收入模型：

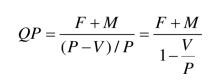
盈亏平衡点（保本）的销售量模型：

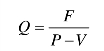
有期望利润的销售量模型：

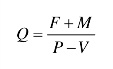
3.经营安全率

经营安全率的计算公式如下：

r=(Y-Y0)/Y=(R-R0)/R

式中：r——经营安全率；

Y0——盈亏平衡的业务量；

R0——盈亏平衡的销售收入；

Y——计划或实现的业务量；

R——计划或实现的销售收入。

当销售量或销售收入越大时，企业经营安全率r就越接近于1，说明企业经营得越好，亏损风险越小；若越接近于0，则表示企业亏损风险越大。企业经营安全率见表3.2。

表3.2　企业经营安全率

【例题3.1】已知某企业甲产品的销售价格为80元/件，单位变动成本为50元/件，固定成本为300 000元，试计算其盈亏临界点。

解：

保本销售量＝300 000/（80－50）＝10 000（件）

保本销售额＝10 000×80＝800 000（元）

或　＝300 000×8/3＝800 000（元）