收集质量数据后需要加以整理，在质量管理中常用的数理统计方法有统计分析表法、分层法、排列图法、因果分析图法、直方图法、散布图法、控制图法等，以上七种方法又称为质量管理的“老七种工具”。此外，还有关系图法、KJ法、系统图法、矩阵图法、网络图法、数据矩阵分析法和PDPC法，统称为“新七种工具”。本文重点介绍“老七种工具”。

1．统计分析表法

统计分析表法是利用专门设计的统计表对质量数据进行收集整理和粗略分析质量状态的一种方法。

在质量控制活动中，利用统计调查表收集数据，简便灵活，便于整理。它没有固定格式，可根据需要和具体情况，设计出不同的统计调查表。常用的有不良项目调查表、缺陷位置调查表、频数调查表、检查确认调查表和施工作业抽样调查表。表5-1为不良项目调查表。

通常，统计分析表分析法同分层法结合起来应用，可以更好、更快地找出问题的原因，以便采取改进的措施。

表5-1　不良项目调查表

2．分层法

分层法也叫分组法或分类法，是把收集到的数据按统计分析的目的和要求进行分类，通过对数据的整理把质量问题系统化、条理化，以便从中找出规律，发现影响质量因素的一种方法。

分层的原则有以下几种:①按不同施工工艺和操作方法分类；②按操作人员或班组分类；③按分部分项工程分类；④按施工时间分类；⑤按设备型号、生产组织分类；⑥按材料成分、规格、供料单位及时间等分类；⑦按其他因素分类，如按检查手段、工作环境等分类。

当分层分得不好时，会使图形的规律性隐蔽起来，还会造成假象。

现举例说明分层法的应用:

某钢筋焊接质量调查数据如下:调查点50个，其中不合格的有19个。已知该批钢筋焊接操作工为三人(A、B、C)，焊条由两个厂家(甲、乙)提供，分析如何提高钢筋焊接质量。

为了查清不合格原因，需要进行分层收集数据。因此分别按工人(见表5-2)、焊条供应厂家(见表5-3)及两者综合分层(见表5-4)进行分类。

表5-2　按工人分层　

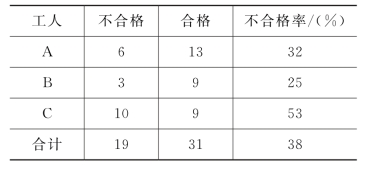
表5-3　按焊条供应厂家分层

表5-4　综合分层分析焊接质量

由分层表5-2和表5-3，人们似乎以为，降低钢筋焊接不合格率的办法可采用乙厂提供的焊条和工人B的操作方法。

而从综合分层表5-4，可知降低钢筋焊接不合格率的措施是:使用甲厂提供的焊条时，要采用工人B的操作方法；使用乙厂提供的焊条时，要采用工人A的操作方法。实践表明，上述的分层法及采用的措施十分有效，不合格率大大降低。

分层法是质量控制统计分析方法中最基本的一种方法。其他统计方法一般都要与分层法配合使用。

3．排列图法

排列图法是把影响产品质量的因素由大到小用矩形表示出来，从而找出影响产品质量的主要问题，以便改进关键项目，又叫帕累托法。

1)排列图的组成

排列图如图5-6所示。

图5-6　排列图

(1)两个纵坐标:左纵坐标表示产品频数(不合格产品件数或造成金额损失数)；右纵坐标表示频率(不合格品件数或损失金额的累计百分率)。

(2)横坐标:影响产品质量的各因素或项目。按影响质量程度大小，由大到小从左到右排列，底宽相同。每个直方形的高度表示该因素影响的大小。

(3)帕累托曲线:表示各影响因素的累计百分数。根据帕累托曲线把影响因素分为三类:

A类因素累积频率0%～80%，是影响产品质量的主要因素；

B类因素累积频率80%～90%，是影响产品质量的次要因素；

C类因素累积频率90%～100%，是影响产品质量的一般因素。重点解决A类质量问题。

2)排列图的绘制步骤

(1)确定分析对象。一般指不合格项目、废品件数、消耗工时等。

(2)收集与整理数据。可按废品项目、缺陷项目、不同操作者等进行分类。列表汇总每个项目发生的数量即频数，按大小进行排列。

(3)计算频数、频率、累计频率。

(4)画图。首先绘出一个横坐标(质量项目)、两个纵坐标(左纵坐标表示频数，右纵坐标表示频率)，然后以频数为高画出各项目的频数直方形，最后从横坐标左端点开始，依次连接各项目直方形右边线及所对应的累计频率值的交点，所得的曲线即为帕累托曲线。

4．因果分析图法

因果分析图又称鱼刺图，它通过带箭头的线，将某个质量问题(结果)与其产生的原因之间的关系表示出来。因果分析图由若干个枝干组成，枝干分为大枝、中枝和小枝，它们分别代表大中小不同的风险因素，一般从人、机械、材料、方法和环境等方面进行分析，如图5-7所示。

因果分析图的绘制步骤与图中箭头方向恰恰相反，是从“结果”开始将原因逐层分解的，具体步骤如下:

(1)明确质量问题——结果，作图时首先由左至右画出一条水平主干线，箭头指向一个矩形框，框内注明研究的问题，即结果。

(2)分析确定影响质量特性大的方面的原因，即4M1E因素。

(3)将每种大原因进一步分解为中原因、小原因，直至分解的原因可以采取具体措施加以解决为止。

(4)检查图中所列的原因是否齐全，集思广益，逐步修改完善。

(5)选择出影响大的关键因素，做出标记“Δ”，以便重点采取措施。

(6)广泛讨论，制定改进的措施和对策，可对应编制一个对策计划表。

例5-1　图5-7为某公司针对隧道开挖(采用光面爆破技术开挖)出现质量缺陷而绘制的因果分析图。

图5-7　隧道施工质量缺陷的因果分析图

该公司QC小组经过集思广益，对其中的主要影响因素制定表5-5所示的对策计划表。

表5-5　对策计划表

5．直方图法

直方图法适用于对大量计量值数据进行整理加工，找出其统计规律，即分析数据分布的形态，以便了解产品质量的波动情况，掌握质量特性的分布规律，估算施工过程中的不合格品率，评价生产过程能力。

1)直方图的绘图步骤

(1)一般收集数据都要随机抽取50个以上质量特性数据，其样本大小用n表示。

例5-2　测得某工程基础混凝土柱施工50个混凝土保护层厚度值(见表5-6)。

表5-6　混凝土保护层厚度测定值整理表(mm)

(2)计算极差R。

本例中，R＝x max－x min＝44 mm－31 mm＝13 mm

(3)确定组数k。

组数常用符号k表示。k与数据多少有关。数据多，多分组；数据少，少分组。

有人用这样一个经验公式计算组数:

本例中n＝50，故:k＝1＋3．31(log n)＝1＋3．31(log50)＝6．62≈7，取k＝7。

(4)求出组距h。

组距即组与组之间的间隔，等于极差除以组数，即

(5)确定组限。

每组的最大值为上限，最小值为下限。为防止数据出现在组限上，无法区分，可采取两种办法:①规定每组上(或下)组限不计算在该组内，而计入相邻较高(或较低)组内；②将组限值较原始数据精度提高半个最小测量单位。本例中:采取第一种方法，即计入较高组。

第一组下限:

第一组上限:30 mm＋h＝30 mm＋2 mm＝32 mm

第二组下限＝第一组上限＝32 mm

第二组上限:32 mm＋2 mm＝34 mm

依次类推。

(6)统计各组频数。

各组频数统计如表5-7所示。(注意:频数总和应等于全部数据个数)

表5-7　频数统计表

(7)绘制频数分布直方图。

图5-8　混凝土保护层厚度分布直方图

在频数分布直方图中，横坐标表示质量特征值，并且标出各组的组限值。根据表5-7可以画出以组距为底，以频数为高的k个直方形，便得到保护层厚度分布直方图(见图5-8)。

2)直方图的观察与分析

(1)观察直方图的形状，判断质量分布状态。

作完直方图后，要认真观察直方图的整体形状，看其是否属于正常型直方图。正常型直方图就是中间高，两侧低，左右对称的图形，如图5-8所示。

出现非正常型直方图时，表明生产过程或收集数据作图有问题。这就要求进一步分析判断，找出原因，从而采取措施加以纠正。非正常型直方图一般有五种类型，如图5-9所示。

①折齿型(见图5-9(b))，是由于分组组数不当或者组距确定不当出现的直方图。

②左(或右)缓坡型(见图5-9(c))，主要是由于操作中对上限(或下限)控制太严造成的。

③孤岛型(见图5-9(d))，是原材料发生变化，或者临时他人顶班作业造成的。

④双峰型(见图5-9(e))，是由于用两种不同方法、两台设备或两组工人进行生产，然后把两个方面的数据混在一起整理产生的。

⑤绝壁型(见图5-9(f))，是由于数据收集不正常，可能有意识地去掉下限以下的数据，或是在检测过程中存在某种人为因素所造成的。

(2)直方图与标准界限比较，判断实际生产过程能力。

作出直方图后，除了观察直方图形状，分析质量分布状态外，再将正常型直方图与质量标准比较，从而判断实际生产过程能力。正常型直方图与质量标准相比较，一般有图5-10所示的六种情况。

图5-10(a)中，B在T中间，质量分布中心与质量标准中心M重合，实际数据分布与标准比较两边还有一定余地，说明生产过程处于正常稳定状态，质量是很理想的。

图5-10(b)中，B虽然在T中间，但是质量分布中心与质量标准中心M不重合，说明如果生产状态一旦发生变化，就可能超出质量标准下限。因此，应采取措施，使直方图移到中间。

图5-9　常见的直方图图形

(a)正常型；(b)折齿型；(c)左缓坡型；(d)孤岛型；(e)双峰型；(f)绝壁型

图5-10　实际质量分析与标准比较(www.daowen.com)

注:T—表示质量标准要求界限；B—表示实际质量特性分布范围

图5-10(c)中，B在T中间，且B的范围接近T的范围，没有余地，说明如果生产状态一旦发生小的变化，就可能超出质量标准。因此，应采取措施，缩小质量分布范围。

图5-10(d)中，B在T中间，但两侧余地太大，说明加工过于精细，不经济。因此，在这种情况下，应适当放宽要求，采取措施适当扩大质量分布范围，从而有利于降低成本。

图5-10(e)中，质量分布B已经超出质量标准下限，说明已出现不合格品。因此，应采取措施进行调整，使质量分布位于标准之内。

图5-10(f)中，质量分布范围完全超出了质量标准的上、下限，散差太大，已经产生许多废品，说明过程能力不足，应采取措施，提高过程能力，缩小质量分布范围。

6．散布图法

散布图又称为相关图。在质量控制中它是用来显示两种质量数据之间关系的一种图形。质量数据之间的关系多属相关关系。

我们可以用Y和X分别表示质量特性值和影响因素，通过绘制散布图，计算相关系数等，分析研究两个变量之间是否存在相关关系，以及这种关系密切程度如何，进而对相关程度密切的两个变量，通过对其中一个变量的观察控制，去估计控制另一个变量的数值，以达到保证产品质量的目的。这种统计分析方法，称为相关图法。

1)相关图的观察与分析

将两个变量有关的数据列出，用点子打在坐标图上，然后观察这两种因素之间的关系，一般有以下六种类型(见图5-11)。

图5-11　相关图的类型

(1)正相关(见图5-11(a))。散布点基本形成由左至右向上变化的一条直线带，即随x增加，y值也相应增加，x与y之间可用直线y＝a＋bx(b为正数)表示。

(2)弱正相关(见图5-11(b))。散布点形成向上较分散的直线带。x增大，y有随之增大的趋势，但是x、y的关系不像正相关那么明确。此时说明除了因素x外，y可能还受其他因素的影响。此时，需要进一步分析其他影响因素。

(3)不相关(见图5-11(c))。散布点形成一团或平行于x轴的直线带。说明x变化不影响y的变化，分析质量原因时可排除x因素。

(4)负相关(见图5-11(d))。散布点形成由左向右下的一条直线带，即x增大，y随之减小。x与y之间可用直线y＝a＋bx(b为负数)表示。

(5)弱负相关(见图5-11(e))。散布点形成由左向右下分布的较分散的直线带。x增大，y基本上随之减小。同样，此时y可能还受其他因素的影响。

(6)非线性相关(见图5-11(f))。散布点呈一曲线带，即在一定范围内，x增加，y也增加；超过这个范围，x增加，y则有下降趋势，或改变变动的斜率呈曲线形态。

2)相关图与相关系数r

变量之间关系的密切程度，需要用一个数量指标来表示，称为相关系数，通常用r表示。不同的相关图有不同的相关系数，r满足:－1≤r≤1。因此，可根据相关系数r值来判断相关图中两个变量之间的关系。

(1)相关系数r的计算公式是:

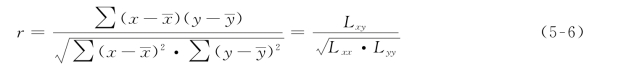
式中，——表示n个x数据的平均值；

——表示n个y数据的平均值；

L xx——表示x的离差平方之和，即；

L yy——表示y的离差平方之和，即；

L xy——表示x的离差平方与y的离差平方的乘积之和，即。

(2)相关系数r的分析判断。

相关系数r的分析判断如表5-8所示。

表5-8　相关系数r的分析判断

7．控制图法

控制图又称为管理图。它是在直角坐标系内画有控制界限，描述生产过程中质量波动状态的图形。利用控制图区分质量波动原因，判明生产过程是否处于稳定状态的方法称为控制图法。

1)控制图概述

(1)控制图的基本形式。

图5-12　控制图的基本形式

控制图的基本形式如图5-12所示。

横坐标为样本(子样)序号或抽样时间，纵坐标为被控制对象，即产品的质量特性值。

控制图上一般有三条平行线:

①实线CL——中心线。

②虚线UCL——上控制界限。

③虚线LCL——下控制界限。

中心线标志着质量特性值分布的中心位置，上、下控制界限标志着质量特性值允许波动的范围。

在生产过程中通过抽样取得数据，把样本统计量描在图上来分析判断生产过程状态。如果点子随机地落在上、下控制界限内，且点子排列无缺陷，则表明生产过程正常，处于稳定状态，不会产生不合格品；如果点子超出控制界限，或点子排列有缺陷，则表明生产条件发生了异常变化，生产过程处于失控状态。此时，必须对过程采取措施，使生产过程恢复正常。

(2)控制图的用途。

它的用途主要有以下两个:

①过程分析，即分析生产过程是否稳定。为此，应随机连续收集数据，绘制控制图，观察数据点分布情况并判定生产过程状态。

②过程控制，即控制生产过程质量状态。为此，要定时抽样取得数据，将其变为点子描在图上，发现并及时消除生产过程中的失调现象，预防不合格品的产生。

与前述排列图法、直方图法等质量控制的静态分析法不同，控制图是典型的动态分析法。通过动态分析法，可以随时了解生产过程中质量的变化情况，及时采取措施，使生产处于稳定状态，起到预防出现废品的作用。

(3)控制图的基本原理。

控制图的设计原理可用三句话来表达，即正态性假定、3σ准则、统计学假设检验理论(即小概率原理和反证法思想)。

①正态性假定。如5．5．1质量统计基本知识所述，任何生产过程生产出来的产品，其质量特征值总会存在一定程度的波动，这些波动主要受到4M1E因素的影响。此时，绝大多数质量特征值均服从或近似服从正态分布。这一假定，称为正态性假定。

②3σ准则。若质量特性X服从正态分布N(μ，σ2)，则有

即(μ－3σ，μ＋3σ)是X的实际取值范围。据此原理，若对X设计控制图，则中心线CL＝μ，上、下控制界限分别为UCL＝μ＋3σ，LCL＝μ－3σ。

③统计学假设检验理论。由3σ准则可知，若质量特性X服从正态分布N(μ，σ2)，则X的可能值超出控制界限的可能性只有0．27%，是小概率事件。而一旦控制图上的点子越出控制界限或其他小概率事件发生，根据统计学假设检验理论，我们有理由怀疑原生产过程失控，也不稳定。

因此，我们可依据描述产品质量分布的集中位置和离散程度的统计特征值，随时间(生产进程)的变化情况来分析生产过程是否处于稳定状态。

2)控制图的分类

(1)按用途分类。

①分析用控制图。主要是用来调查分析生产过程是否处于控制状态。绘制分析用控制图时，一般需要连续抽取20～25组样本数据，计算控制界限。

②管理(或控制)用控制图。主要用来控制生产过程，使之经常保持在稳定状态。通常是把分析用控制图的控制界限延长作为管理用控制图的控制界限，并按一定的时间间隔取样、计算、打点，根据点子分布情况，判断生产过程是否有异常原因影响。

(2)按质量数据特点分类。

①计量值控制图。主要适用于质量特性值属于计量值的控制。常用的计量值控制图有以下几种控制图控制图；x－Rs控制图控制图。

②计数值控制图。通常用于控制质量数据中的计数值，如不合格品数、疵点数、不合格品率、单位面积上的疵点数等离散型变量。根据计数值的不同又可分为计件值控制图和计点值控制图。计件值控制图有不合格品数P n控制图和不合格品率p控制图。计点值控制图有缺陷数c控制图和单位缺陷数u控制图。

3)控制图的观察与分析

绘制控制图的目的是分析判断生产过程是否处于稳定状态。当控制图同时满足以下两个条件:①点子几乎全部落在控制界限之内；②控制界限内的点子排列没有缺陷，我们就可以认为生产过程基本上处于稳定状态。如果点子的分布不满足其中任何一条，都应判断生产过程为异常。

(1)点子几乎全部落在控制界限内，是指应符合下述三个要求:

①连续25点以上处于控制界限内。

②连续35点中仅有1点超出控制界限。

③连续100点中不多于2点超出控制界限。

(2)点子排列没有缺陷，是指点子的排列是随机的，而没有出现异常现象。这里的异常现象是指点子排列出现了“链”“多次同侧”“趋势或倾向”“周期性变动”“接近控制界限”等情况，如图5-13所示。

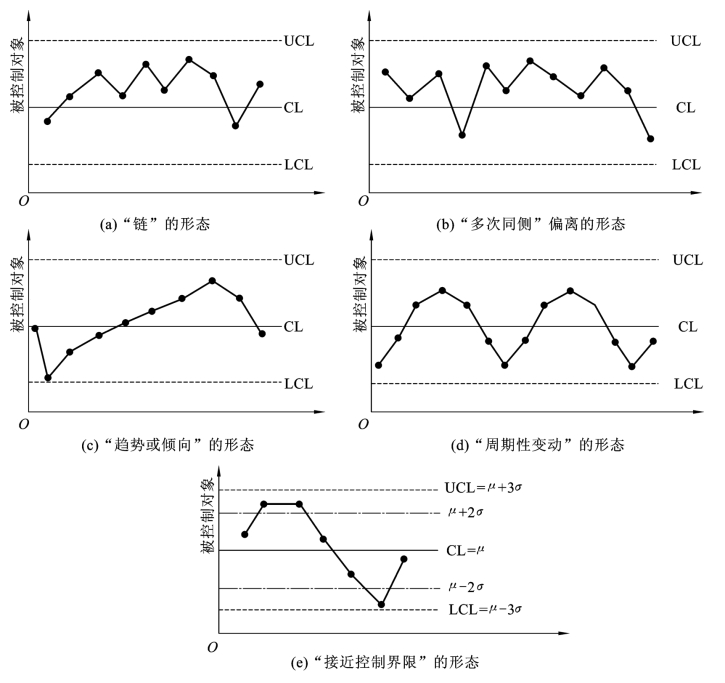
图5-13　点子排列有缺陷的形态

①链:是指点子连续出现在中心线一侧的现象。出现五点链，应注意生产过程发展状况；出现六点链，应开始调查原因；出现七点链，应判定工序异常，需要采取处理措施(见图5-13(a))。

②多次同侧:是指点子在中心线一侧多次出现的现象，或称偏离。下列情况说明生产过程已出现异常:在连续11点中有10点在同侧(见图5-13(b))；在连续14点中有12点在同侧；在连续17点中有14点在同侧；在连续20点中有16点在同侧。

③趋势或倾向:是指点子连续上升或连续下降的现象。连续7点或7点以上上升或下降排列，就应判定生产过程有异常因素影响，要立即采取措施(见图5-13(c))。

④周期性变动:是指点子的排列显示周期性变化的现象。这样即使所有点子都在控制界限内，也应认为生产过程为异常(图5-13(d))。

⑤接近控制界限:是指点子落在了μ±2σ以外和μ±3σ以内。如属下列情况，判定为异常:连续3点至少有2点接近控制界限；连续7点至少有3点接近控制界限(见图5-13(e))；连续10点至少有4点接近控制界限。

思考题

1.简述质量及工程项目质量的定义。

2.简述工程项目质量管理及质量控制的定义和主要内容。

3.简述工程项目进展各阶段对其质量的影响。

4.试述影响工程项目质量的主要因素。

5.工程项目质量控制应遵循哪些基本原理?

6.简述GB/T19000—ISO9000—2016系列标准的适用范围。

7.简述GB/T19000—ISO9000—2016系列标准质量管理的原则。

8.简要说明质量管理体系建立与运行的程序。

9.简要说明质量管理体系认证的意义、特征和主要实施程序。

10.简述质量统计推断工作过程。

11.描述质量数据集中趋势与离中趋势分别有哪些参数?

12.简述质量数据波动的原因及其分布的统计规律。

13.质量控制七种统计方法的用途各有哪些?

14.简述排列图的绘制步骤及其作用。

15.试述因果分析图的基本原理和绘图步骤。

16.如何绘制直方图并对其进行观察分析?

17.如何根据控制图判断项目质量状态?

18.简述工程参与各方在施工阶段的质量控制目标。

19.施工质量控制的依据主要有哪些方面?

20.简述现行施工质量计划的主要形式和基本内容。

21.什么是质量控制点?选择质量控制点的原则是什么?

22.简述生产要素质量控制的主要内容。

23.施工工序质量控制的基本要求有哪些?

24.现场质量检查的主要内容和方法是什么?

25.施工过程中成品保护的措施一般有哪些?