1．总体、样本及统计推断工作过程

1)总体

总体也称母体，是所研究对象的全体。个体，是组成总体的基本元素。总体中含有个体的数目通常用N表示。

2)样本

样本也称子样，是从总体中随机抽取出来，并根据对其研究结果推断总体质量特征的那部分个体。被抽中的个体称为样品，样品的数量叫样本容量，用n表示。

3)统计推断工作过程

质量统计推断工作是运用质量统计方法在生产过程中或一批产品中，随机抽取样本，通过对样品进行检测和整理加工，从中获得样本质量数据信息，并以此为依据，以概率数理统计为理论基础，对总体的质量状况做出分析和判断。质量统计推断工作过程如图5-5所示。

图5-5　质量统计推断工作过程

2．质量数据的收集方法

1)全数检验

全数检验是对总体中的全部个体逐一观察、测量、计数、登记，从而获得对总体质量水平评价结论的方法。

全数检验一般比较可靠，能提供大量的质量信息，但要消耗很多人力、物力、财力和时间，特别是不能用于具有破坏性的检验和过程质量控制，应用上具有局限性。

2)随机抽样检验

抽样检验是按照随机抽样的原则，从总体中抽取部分个体组成样本，根据对样品进行检测的结果，推断总体质量水平的方法。

抽样检验抽取样品不受检验人员主观意愿的支配，每一个体被抽取的概率都相同，从而保证了样本在总体中的分布比较均匀，有充分的代表性。同时它还具有节省人力、物力、财力、时间和准确性高的优点。它还可用于破坏性检验和生产过程的质量监控，具有广泛的应用空间。抽样的具体方法有简单随机抽样、分层抽样、等距抽样、整群抽样和多阶段抽样等。

3．质量数据的分类

质量数据是指由个体产品质量特性值组成的样本(总体)的质量数据集，在统计上称为变量；个体产品质量特性值称为变量值。根据质量数据的特点，可以将其分为计量值数据和计数值数据。

1)计量值数据

计量值数据是可以连续取值的数据，属于连续型变量。其特点是在任意两个数值之间都可以取精度较高一级的数值。它通常由测量得到，如重量、强度、几何尺寸、位移等。

2)计数值数据

计数值数据是只能按0，1，2，…数列取值计数的数据，属于离散型变量。它一般由计数得到。计数值数据又可分为计件值数据和计点值数据:

(1)计件值数据，表示具有某一质量标准的产品个数，如总体中合格品数。

(2)计点值数据，表示个体(单件产品、单位长度、单位面积、单位体积等)上的缺陷数、质量问题点数等。如检验钢结构构件涂料涂装质量时，构件表面的焊渣、焊疤、毛刺的数量等。

4．质量数据的特征值(www.daowen.com)

常用的有描述数据分布集中趋势的算术平均数、中位数和描述数据分布离中趋势的极差、标准偏差、变异系数等。

1)描述数据集中趋势的特征值

(1)算术平均数。

算术平均数又称均值，是消除了个体之间个别偶然的差异，显示出所有个体共性和数据一般水平的统计指标。以样本数据特征值为例，其计算公式为:

式中，n——样本容量；

x i——样本中第i个样品的质量特征值。

(2)样本中位数。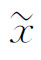

它是指将样本数据按数值大小有序排列后，位置居中的数值。当样本数n为奇数时，数列居中的那位数即为中位数；当样本数n为偶数时，取居中两个数的平均值作为中位数。

(3)众数。

它是指一批样本数据中，与最高频数所对应的数值。在频率分布图中，众数就是分布曲线的顶点所对应的数值。

2)描述数据离中趋势的特征值

(1)极差R。

极差是数据中最大值与最小值之差，是用数据变动的幅度来反映其分散状况的特征值。极差计算简单、使用方便，但粗略，数值仅受两个极端值的影响，损失的质量信息多，仅适用于小样本。其计算公式为:

(2)标准偏差。

标准偏差简称标准差或均方差，是个体数据与均值离差平方和的算术平均数的算术根，是大于0的正数。它能确切说明数据分布的离散程度和波动规律，是最常用的反映数据变异程度的特征值。以样本数据特征值为例，样本的标准偏差S的计算公式为:

(3)变异系数Cv。

变异系数又称离散系数，是用标准差除以算术平均数得到的相对数。它表示数据的相对离散波动程度。变异系数小，说明分布集中程度高，离散程度小，均值对总体(样本)的代表性好。以样本数据特征值为例，样本的变异系数计算公式为:

5．质量数据的统计规律

如前所述，工程项目质量通常受到4M1E因素的影响，项目质量数据因此具有波动性。质量特性值的变化在质量标准允许范围内波动称为正常波动，是由偶然性原因引起的；若是超越了质量标准允许范围的波动则称为异常波动，是由系统性原因引起的，在生产中应该随时监控，及时识别和处理。

在众多偶然随机因素的影响下，质量数据的分布通常符合某种统计规律。概率数理统计在对大量统计数据研究中，归纳总结出许多分布类型，如一般计量值数据服从正态分布，计件值数据服从二项分布，计点值数据服从泊松分布等。实践中只要是受许多起微小作用的因素影响的质量数据，都可认为是近似服从正态分布的，如构件的几何尺寸、混凝土强度等；如果是随机抽取的样本，无论它来自的总体是何种分布，在样本容量较大时，其样本均值也服从或近似服从正态分布。因而，正态分布是最重要、最常见、应用最广泛的分布。