工程网络计划分析主要是进行时间参数计算，识别关键工作和关键线路，并利用非关键工作的时差。

1．基本概念

1)时间参数

(1)最早开始时间(early start time，ES)，指在紧前工作和有关时限约束下，工作有可能开始的最早时刻。

(2)最早完成时间(early finish time，EF)，指在紧前工作和有关时限约束下，工作有可能完成的最早时刻。

(3)最迟开始时间(late start time，LS)，指在不影响任务按期完成和有关时限约束下，工作最迟必须开始的时刻。

(4)最迟完成时间(late finish time，LF)，指在不影响任务按期完成和有关时限约束下，工作最迟必须完成的时刻。

(5)总时差(total float，TF)，指在不影响工期和有关时限的前提下，一项工作可以利用的机动时间。

(6)自由时差(free float，FF)，指在不影响其紧后工作最早开始和有关时限的前提下，一项工作可以利用的机动时间。

图4-16　双代号网络计划时间参数关系示意图

双代号网络计划图中，紧前工作最早开始时间ES i—j、紧前工作最早完成时间EF i—j、紧后工作最早开始时间EF j—k、紧后工作最迟开始时间LS j—k、自由时差FF i—j、总时差TF i—j之间的关系如图4-16所示。

2)工期

(1)计算工期(calculated project duration，T c)，指根据网络计划时间参数计算所得到的工期。

(2)要求工期(required project duration，T r)，指任务委托人所提出的指令性工期。

(3)计划工期(planned project duration，T p)，指在要求工期和计算工期的基础上综合考虑需要和可能而确定的工期。

3)关键工作与关键线路

(1)关键工作，指网络计划中总时差(TF)最少的工作。

(2)关键线路。在双代号网络计划中，由关键工作组成的线路或总持续时间最长的线路；在单代号网络计划中，由关键工作组成，且关键工作之间的间隔时间为零的线路或总持续时间最长的线路。

2．双代号网络计划

双代号网络计划分析主要包括计算时间参数和确定关键工作与关键线路，下面将分别进行阐述。

1)六时标法计算

采用六时标法，需要计算每项工作的六个时间参数。该方法计算最为完整，但计算工作量也较大。学习网络计划技术，应首先掌握六时标计算方法。在计算各项工作的时间参数之前，应先确定各项工作的持续时间Di—j。虚工作可视同工作进行计算，但其持续时间为零。工作时间参数的计算结果应分别标注(见图4-17)。

图4-17　工作时间参数的计算结果的标注

(1)计算工作最早开始时间ES i—j和最早完成时间EF i—j。

由于工作最早时间参数受到其紧前工作的约束，因此，工作最早开始时间和最早完成时间的计算应从网络计划的起点节点开始，顺着箭线方向依次逐项计算。其中，虚工作可视同工作进行计算，其持续时间应为零。

以起点节点1为箭尾节点的工作i—j，当未规定其最早开始时间ES i—j时，应按下式计算:

ES i—j＝0(当i＝1)

工作i—j的最早完成时间等于最早开始时间加上持续时间D i—j:

EF i—j＝ES i—j＋Di—j

其他工作的最早开始时间等于各紧前工作i—j的最早完成时间EF i—j的最大值:

ES j—k＝max(EF i—j)，　或　ES j—k＝max(ES i—j＋Di—j)

(2)确定计算工期T c。

当网络计划终点节点的编号为n时，计算工期为:

T c＝max(EF m—n)

网络计划的计划工期(T p)应按下列情况确定:

①当已规定要求工期(T r)时:

T p≤T r

②当未规定要求工期(T r)时:

T p＝T c

(3)计算工作最迟完成时间LF i—j和最迟开始时间LS i—j。由于工作最迟时间参数受到其紧后工作的约束，因此，工作最迟完成时间和最迟开始时间的计算应从网络计划的终点节点开始，逆着箭线方向依次逐项计算。

以网络计划的终点节点n为箭头节点的工作，其最迟完成时间LF i—j等于计划工期T p，即

LF i—j＝T p(当j＝n)

其他工作的最迟完成时间LF i—j等于其紧后工作的最迟开始时间LS j—k的最小值，即

LF i—j＝min(LS j—k)，　或　LF i—j＝min(LF j—k－Dj—k)

工作i—j的最迟开始时间等于其最迟完成时间减去其持续时间:

LS i—j＝LF i—j－Di—j

(4)计算工作总时差TF i—j和自由时差FF i—j。

工作总时差等于其最迟开始时间与最早开始时间之差，或最迟完成时间与最早完成时间之差:

TF i—j＝LS i—j－ES i—j

TF i—j＝LF i—j－EF i—j

当工作i—j有紧后工作j—k时，其自由时差应为:

FF i—j＝min(ES j—k)－EF i—j

以网络计划的终点节点(j＝n)为箭头节点的工作，其自由时差为:

FF i—n＝T c－EF i—n

例4-2　某工程项目的双代号网络计划图如图4-18所示，请用工作法计算各时间参数。

图4-18　某工程双代号网络计划图

分析步骤为:

(1)最早时间计算。

从网络计划的起点节点开始，顺着箭线方向，计算每项工作的最早开始时间和最早完成时间。这是一种最积极、最快速的施工安排，依据前述公式依次可计算得出:

①以起点节点1为箭尾节点的工作1—2，1—4，1—3:

ES1—2＝0　EF1—2＝ES1—2＋D 1—2＝0＋4＝4

ES1—4＝0　EF1—4＝ES1—4＋D 1—4＝0＋5＝5

ES1—3＝0　EF1—3＝ES1—3＋D 1—3＝0＋6＝6

②中间工作2—6，4—5，3—7:

ES2—6＝EF1—2＝4　EF2—6＝ES2—6＋D 2—6＝4＋4＝8

ES4—5＝max{EF1—2，EF1—4，EF1—3}＝max{4，5，6}＝6

EF4—5＝ES4—5＋D 4—5＝6＋5＝11

ES3—7＝EF1—3＝6　EF3—7＝ES3—7＋D 3—7＝6＋4＝10

③工作6—8，7—8:

ES6—8＝max{EF2—6，EF4—5}＝max{8，11}＝11

EF6—8＝ES6—8＋D 6—8＝11＋6＝17

ES7—8＝max{EF4—5，EF3—7}＝max{11，10}＝11

EF7—8＝ES7—8＋D 7—8＝11＋5＝16

(2)总工期的确定。

T c＝max[EF6—8，EF7—8]＝max[17，16]＝17

(3)最迟时间计算。

从网络计划的终点节点开始，逆着箭线方向，倒排工期计划。由于本题未给出T p值，因而T p＝T c＝17倒排，也就是最后一个节点的最迟完成时间为17，向前倒排，依次计算得出:

①以终点节点8为箭头节点的工作6—8，7—8:

LF6—8＝T c＝17　LS6—8＝LF6—8－D 6—8＝17－6＝11

LF7—8＝T c＝17　LS7—8＝LF7—8－D 7—8＝17－5＝12

②中间工作2—6，4—5，3—7:

LF2—6＝LS6—8＝11　LS2—6＝LF2—6－D 2—6＝11－4＝7

LF4—5＝min{LS6—8，LS7—8}＝min{11，12}＝11

LS4—5＝LF4—5－D 4—5＝11－5＝6

LF3—7＝LS7—8＝12　LS3—7＝LF3—7－D 3—7＝12－4＝8

③起始工作1—2，1—4，1—3:

LF1—2＝min{LS2—6，LS4—5}＝min{7，6}＝6

LS1—2＝LF1—2－D 1—2＝6－4＝2

LF1—4＝LS4—5＝6　LS1—4＝LF1—4－D 1—4＝6－5＝1

LF1—3＝min{LS4—5，LS3—7}＝min{6，8}＝6

LS1—3＝LF1—3－D 1—3＝6－6＝0

(4)总时差计算。

从网络计划的起点节点开始，顺着箭线方向，依次取最大值可计算得出:

TF1—2＝LS1—2－ES1—2＝2－0＝2

或TF1—2＝LF1—2－EF1—2＝6－4＝2

同理:　TF1—4＝1　TF1—3＝0　TF2—6＝3　TF4—5＝0

TF3—7＝2　TF6—8＝0　TF7—8＝1

(5)自由时差计算。

从网络计划的终点节点开始，逆着箭线方向，依次取最小值可计算得出:

FF6—8＝T c－EF6—8＝17－17＝0

FF7—8＝T c－EF7—8＝17－16＝1

FF2—6＝ES6—8－EF2—6＝11－8＝3

FF4—5＝min{ES6—8，ES7—8}－EF4—5＝min{11，11}－11＝0

FF3—7＝ES7—8－EF3—7＝11－10＝1

同理:　FF1—2＝0　FF1—4＝1　FF1—3＝0

(6)图上计算标识法。

双代号网络计划图计算熟练之后，一般不需要列出以上冗长的计算公式和步骤，而是采用图上计算法，依次在图上计算和标出六个时间参数，如图4-19所示。注意，还需要将六个时间参数的排列顺序在图上标出，避免混淆。

2)标号法(也称节点法)

由于六时标法的计算工作量大，步骤烦琐，容易出错。在工程项目计划中，有时不需要全部六个时间参数，而需要快速计算总工期和寻找关键线路，此时可采用标号法。一般在每个节点j上只标注一个时间参数ET i和前一个节点的编号。节点标注时间ET i应从网络计划的起点节点开始，顺着箭线方向依次逐项计算。当未规定最早时间时，起点节点i的最早时间应按下式计算:

图4-19　工作时间在图上计算法的标注

ET i＝0(i＝1)

其他节点j的最早时间(ET j)应按下式计算:

ET j＝max(ET i＋Di—j)

网络计划的计算工期T c应按下式确定，其中n为网络计划的终点节点:

T c＝ET n

标号法的计算步骤为:

(1)按节点法计算各节点的最早时间(ET j)，即节点标号值。

(2)用节点标号值及其源节点对节点进行双标号；当有多个源节点时，应将所有源节点标注出来。

(3)网络计划的计算工期(T c)即为网络计划终点节点(n)的标号值。

(4)按已标注出的各节点标号值的来源，从终点节点向起点节点逆向搜索，标号值最大的节点相连，即可确定关键线路。

例4-3　计算图4-20所示双代号网络计划图的计算工期，并确定关键线路。

图4-20　某双代号网络计划图

此题只需确定计算工期和关键线路，并不需要计算各项工作的时间参数，因此，采用节点标号法，分析步骤如下:

(1)计算节点最早时间(ET j)。

ET1＝0

ET 2＝ET 1＋D 1—2＝0＋5＝5

ET 3＝ET 2＋D 2—3＝5＋8＝13

ET4＝max(ET2＋D 2—4，ET3＋D 3—4)＝max(5＋6，13＋2)＝max(11，15)＝15

ET 5＝max(ET 3＋D 3—5，ET 4＋D 4—5)＝max(13＋4，15＋0)＝max(17，15)＝17

ET 6＝max(ET 4＋D 4—6，ET 5＋D 5—6)＝max(15＋5，17＋1)＝max(20，18)＝20

ET 7＝max(ET 5＋D 5—7，ET 6＋D 6—7)＝max(17＋7，20＋3)＝max(24，23)＝24

ET 8＝ET 7＋D 7—8＝24＋8＝32

(2)网络图标号。

将计算出的节点最早时间(ET j)及其源节点对节点进行双标号(见图4-21)。

图4-21　网络图的节点标注

(3)确定计算工期T c。

T c＝ET 8＝32

(4)确定关键线路。(www.daowen.com)

从终点节点向起点节点逆向搜索，标号值最大的节点相连，即可确定关键线路(见图4-22):①→②→③→⑤→⑦→⑧。

图4-22　网络图的关键线路

3．单代号网络计划

单代号网络计划的时间参数计算应在确定各项工作持续时间之后进行。单代号网络计划的时间参数应分别标注(见图4-23)。

1)工作最早时间

工作i的最早开始时间(ES i)应从网络计划的起点节点开始顺着箭线方向依次逐项计算。

图4-23　单代号网络计划时间参数的标注

(i，j—节点编号；A、B—工作；Di，Dj—持续时间；ES i，ES j—最早开始时间；EF i，EF j—最早完成时间；LS i，LS j—最迟开始时间；LF i，LF j—最迟完成时间；TF i，TF j—总时差；FF i，FF j—自由时差；LAG i，j—间隔时间)

当起点节点i的最早开始时间(ES i)无规定时，应按下式计算:

ES i＝0(当i＝1)

其他工作i的最早开始时间(ES i)应按下式计算:

ES i＝max(ES h＋D h)＝max(EF h)

式中，ES i—工作i的最早开始时间；

ES h—工作i的各项紧前工作h的最早开始时间；

D h—工作i的各项紧前工作h的持续时间；

EF h—工作i的各项紧前工作h的最早完成时间。

工作i的最早完成时间(EF i)应按下式计算:

EF i＝ES i＋Di

2)工期计算

网络计划计算工期(T c)应按下式计算:

T c＝EF n

式中，EF n——终点节点n的最早完成时间。

网络计划的计划工期T p，应按下列情况确定:

(1)当已规定要求工期(T r)时:

T p≤T r

(2)当未规定要求工期(T r)时:

T p＝T c

(3)相邻两项工作i和j之间的间隔时间(LAG i，j)的计算应符合下列规定:

①当终点节点为虚拟节点时，其间隔时间应按下式计算:

LAG i，n＝T p－EF i

②其他节点之间的间隔时间应按下式计算:

LAG i，j＝ES j－EF i

3)工作总时差

工作i的总时差(TF i)应从网络计划的终点节点开始，逆着箭线方向依次逐项计算。终点节点所代表工作n的总时差(TF n)应按下式计算:

TF n＝T p－EF n

其他工作i的总时差(TF i)应按下式计算:

TF i＝min(TF j＋LAG i，j)

4)工作自由时差

终点节点所代表的工作n的自由时差(FF n)应按下式计算:

FF n＝T c－EF n

其他工作i的自由时差(FF i)应按下式计算:

FF i＝min(LAG i，j)

5)工作最迟完成时间

工作i的最迟开始时间(LS i)、最迟完成时间(LF i)应按下列公式计算:

LS i＝ES i＋TF i

LF i＝EF i＋TF i

例4-4　计算图4-24所示的单代号网络计划的计算工期，并确定关键线路。

图4-24　某单代号网络计划图

分析步骤如下:

(1)最早时间计算。

从网络计划的起点节点开始，顺着箭线方向，依次取最大值可计算得出:

槽1:ES11＝0　EF11＝ES11＋D 11＝0＋3＝3

槽2:ES12＝EF11＝3　EF12＝ES12＋D 12＝3＋3＝6

槽3:ES13＝EF12＝6　EF13＝ES13＋D 13＝6＋3＝9

垫1:ES21＝EF11＝3　EF21＝ES21＋D 21＝3＋3＝6

垫2:ES22＝max(EF12，EF21)＝max(6，6)＝6

EF22＝ES22＋D 22＝6＋3＝9

垫3:ES23＝max(EF13，EF22)＝max(9，9)＝9

EF23＝ES23＋D 23＝9＋3＝12

基1:ES31＝EF21＝6　EF31＝ES31＋D 31＝6＋5＝11

基2:ES32＝max(EF22，EF31)＝max 9，11{　}＝11

EF32＝ES32＋D 32＝11＋5＝16

基3:ES33＝max(EF23，EF32)＝max 12，16{　}＝16

EF33＝ES33＋D 33＝16＋5＝21

填1:ES41＝EF31＝11　EF41＝ES41＋D 41＝11＋2＝13

填2:ES42＝max(EF32，EF41)＝max(16，13)＝16

EF42＝ES42＋D 42＝16＋2＝18

填3:ES43＝max(EF33，EF42)＝max(21，18)＝21

EF43＝ES43＋D 43＝21＋2＝23

(2)总工期的确定。

最早时间和总工期计算如图4-25所示。

T c＝EF43＝23

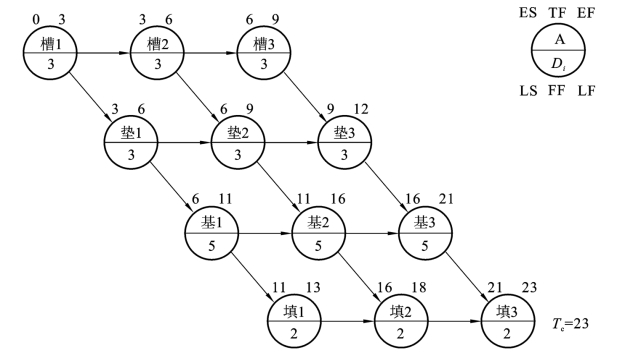
图4-25　最早时间和总工期计算

(3)间隔时间(LAG i，j)计算。

从图4-26可知，间隔时间只存在于垫2→基2、垫3→基3、填1→填2、填2→填3四处:

垫2→基2:LAG22，32＝ES32－EF22＝11－9＝2

垫3→基3:LAG23，33＝ES33－EF23＝16－12＝4

填1→填2:LAG41，42＝ES42－EF41＝16－13＝3

填2→填3:LAG42，43＝ES43－EF42＝21－18＝3

(4)工作总时差计算。

填3:TF43＝T p－EF43＝23－23＝0

填2:TF42＝TF43＋LAG42，43＝0＋3＝3

填1:TF41＝TF42＋LAG41，42＝3＋3＝6

基3:TF33＝TF43＋LAG33，43＝0＋0＝0

基2:TF32＝min(TF33＋LAG32，33，TF42＋LAG32，42)＝min(0＋0，3＋0)＝0

基1:TF31＝min(TF32＋LAG31，32，TF41＋LAG31，41)＝min(0＋0，6＋0)＝0

垫3:TF23＝TF33＋LAG23，33＝0＋4＝4

垫2:TF22＝min(TF23＋LAG22，23，TF32＋LAG22，32)＝min(4＋0，0＋2)＝2

垫1:TF21＝min(TF22＋LAG21，22，TF31＋LAG21，31)＝min(2＋0，0＋0)＝0

槽3:TF13＝TF23＋LAG13，23＝4＋0＝4

槽2:TF12＝min(TF13＋LAG12，13，TF22＋LAG12，22)＝min(4＋0，2＋0)＝2

槽1:TF11＝min(TF12＋LAG11，12，TF21＋LAG11，21)＝min(2＋0，0＋0)＝0

(5)工作自由时差计算。

终点节点所代表的工作“填3”的自由时差FF43＝T p－EF43＝23－23＝0

其他工 作i的 自 由 时 差FF i＝min(LAG i，j)，由 于 只 有LAG22，32、LAG23，33、LAG41，42和LAG42，43不为0，因此，除以下几项工作外，其余工作自由时差均为0。

垫3:FF23＝LAG23，33＝4

填1:FF42＝LAG42，43＝3

填2:FF41＝LAG41，42＝3

(6)工作最迟完成时间。

从网络计划的终点节点开始，逆着箭线方向，如图4-26所示，依次取最小值可计算得出:

图4-26　六参数计算结果标注

填3:LF43＝EF43＋TF43＝23＋0＝23

填2:LF42＝EF42＋TF42＝18＋3＝21

填1:LF41＝EF41＋TF41＝13＋6＝19

基3:LF33＝EF33＋TF33＝21＋0＝21

基2:LF32＝EF32＋TF32＝16＋0＝16

基1:LF31＝EF31＋TF31＝11＋0＝11

垫3:LF23＝EF23＋TF23＝12＋4＝16

垫2:LF22＝EF22＋TF22＝9＋2＝11

垫1:LF21＝EF21＋TF21＝6＋0＝6

槽3:LF13＝EF13＋TF13＝9＋4＝13

槽2:LF12＝EF12＋TF12＝6＋2＝8

槽1:LF11＝EF11＋TF11＝3＋0＝3

4．双代号时标网络计划

双代号时标网络计划兼有网络计划和横道图计划的优点，能够清楚地表明计划的时间进程，各项工作的开始与完成时间、工作的自由时差及关键线路可以在图上直接显示出来，因此，双代号时标网络计划的分析比较简单。

(1)双代号时标网络计划的计算工期，应为计算坐标体系中终点节点与起点节点所在位置的时标值之差。

(2)按最早时间绘制的双代号时标网络计划，箭尾节点中心所对应的时标值为工作的最早开始时间；当箭线不存在波形线时，箭头节点中心所对应的时标值为工作的最早完成时间；当箭线存在波形线时，箭线实线部分的右端点所对应的时标值为工作的最早完成时间。

(3)工作的自由时差应为工作的箭线中波形线部分在坐标轴上的水平投影长度。

(4)双代号时标网络计划工作总时差的计算应自右向左进行，并应符合下列规定。

①以终点节点(j＝n)为箭头节点的工作，总时差(TF i—n) 应按下式计算:

TF i—n＝T n－EF i—n

②其他工作i—j的总时差应按下式计算:

TF i—j＝min(TF j—k＋FF i—j)

式中，TF j—k——工作i—j的紧后工作j—k的总时差。

(5)双代号时标网络计划中工作的最迟开始时间和最迟完成时间，应按下列公式计算:

LS i—j＝ES i—j＋TF i—j

LF i—j＝EF i—j＋TF i—j

(6)双代号时标网络计划中，自起点节点至终点节点不出现波形线的线路，应确定为关键线路。关键线路上的工作即为关键工作。

例4-5　计算图4-27所示双代号时标网络计划中各工作的总时差，并确定关键线路。

图4-27　某双代号时标网络计划图

在双代号时标网络计划中，自始至终不出现波形线的线路为关键线路:①→②→③→⑤→⑦→⑧→⑨。

关键线路上的工作均为关键工作，其总时差为0，因此，仅需计算非关键工作的总时差，自右向左依次计算如下:

工作J:TF7—9＝T 9－EF7—9＝12－11＝1

工作H:TF6—9＝T 9－EF6—9＝12－10＝2

工作F:TF4—8＝TF8—9＋FF4—8＝0＋2＝2

工作E:TF2—6＝TF6—9＋FF2—6＝2＋0＝2

工作B:TF1—3＝TF3—5＋FF1—3＝0＋1＝1

工作A:TF1—4＝min(TF4—8＋FF1—4，TF4—5＋FF1—4)＝min(2＋0，1＋0)＝1