厂址选择的优劣直接影响工程设计质量、建设进度、投资额大小和投产后经营管理条件，进行多方案的比较是十分必要的。

厂址方案比较有很多种方案，其中最常用的有重要因素排除法、法案比较法和统计学法。

（一）重要因素排除法

备选厂址对应重要因素的条件凡不能满足国家规定及工程技术要求的，均不再参与比选；有可能严重影响厂址选择的重要因素的，经过调研讨论无法解决，也不再参与比选。

1．不能满足国家规定及工程技术要求的重要因素

（1）不符合国家产业布局、地方发展规划。

（2）在有地质灾害地区内，如基本烈度高于七度地区、海啸区、泥石流严重危害区。

（3）在采矿沉陷区或具有开采价值的矿藏区内。

（4）在国家规定的自然保护区、历史文物区内等。

2．有可能严重影响厂址选择的重要因素

（1）不符合卫生防护距离或安全防护距离。

（2）公用工程供应不可靠，如电力供应不足等。

（3）交通运输能力不足。

（4）不能得到当地公众支持与舆论支持。

（二）方案比较法

方案比较法，就是以技术经济条件为主体，列出其中若干条件作为主要影响因素，形成厂址方案。然后对每一方案的优缺点进行比较，最后结合以往的选择厂址经验，得出最佳厂址的选择结论。对工业企业而言，厂址选择往往是以总成本最小为决策目标。

基本思路是从经济上进行分析，以费用（或成本）大小作为择优标准。费用由基本建设和经营费用两部分组成。利用这种方法，首先是在建厂地区内选择几个厂址，列出可比因素，进行初步分析；比较后选出两三个较为合适的大体方案，然后进行详细的调查、勘察、列出厂址方案比较表、计算各方案的建设费用和经营费用。通过分析进而选择投资回收期较短或年等值费用最小的方案。

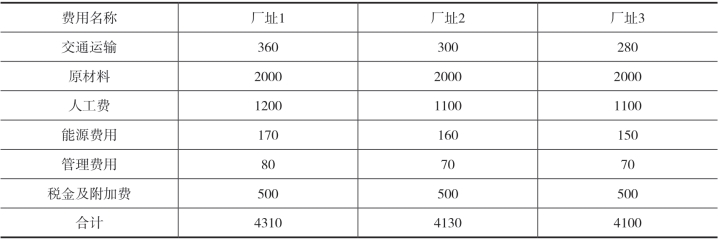
以某服装厂为例，其选址方案有三个，列表得到三个方案的建设费用（见表2-2）和经营费用（见表2-3），计算得到年等值费用最小的方案为最佳方案。

表2-2　备选厂址建设费用比较　单位：万元

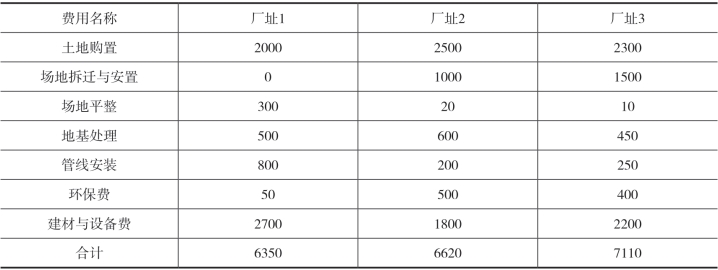
表2-3　备选厂址每年经营费用比较　单位：万元

需要把建设投资的费用折换成年等值费用，等额资金回收系数K公式为：

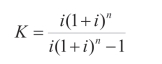
式中：K——资金回收系数；

i——投资年利率；

n——计算期，单位年。

按照计算期10年，投资年利率按6.55%计算，则3个备选厂址的计算如下：

K=0.1394

厂址1的年总成本=6350×0.1394＋4310= 5195.19（万元）

厂址2的年总成本=6620×0.1394＋4130= 5052.83（万元）

厂址3的年总成本=7110×0.1394＋4100= 5091.13（万元）

综上所述，厂址2是年总成本最少的方案，所以最终选择厂址2为最佳方案。

（三）统计学方法

厂址最优位置确定的统计学方法有：比较矩阵法、层次分析法、判定优先次序法、重心法及数学程序法、数学规划法、评分优选法、模糊综合评判法等。以上方法可以分为两类：第一类，没有候选的厂址位置，通过建立基于某种或某几种目标的数学模型来直接寻求最优厂址位置，如重心法、数学程序法及数学规划法；第二类，通过定性分析建立候选厂址位置集合，进而通过分析候选集合中各厂址的各项指标（包括定性指标与定量指标），得到各厂址的综合评价值，并在其中择优作为确定的厂址最优位置。如比较矩阵法、层次分析法、模糊综合评判法等。各种方法均有其自身的特点和适应性。

目前，层次分析法运用最广泛，也较为简单。它能够在已确定的地点内，通过对比数个候选集合中的各厂址位置的各项指标属性，得到其综合评价值，并据此选择厂址最优位置。

1．层次分析法（Analytic Hierarchy Process，简称AHP）

是美国运筹学家于20世纪80年代提出的一种实用的多方案或多目标的决策方法。其主要特征是，它合理地将定性与定量的决策结合起来，按照思维、心理的规律把决策过程层次化、数量化。

用AHP分析问题大体要经过以下五个步骤：

（1）建立层次结构模型，确定层次间关系，见图2-6。

（2）通过相互比较确定各准则对于目标的权重，即构造判断矩阵。在层次分析法中，为使矩阵中的各要素的重要性能够进行定量显示，引进了矩阵判断标度（1～9标度法）。对于要比较的因子而言，认为一样重要就是1∶1，强烈重要就是9∶1，也可以取中间数值6∶1等，两两比较，把数值填入，并排列成判断矩阵（判断矩阵是对角线积是1的正反矩阵即可）。(www.daowen.com)

图2-6　层次结构模型

（3）需要对层次单排序。层次单排序是指对于上一层某因素而言，本层次各因素的重要性的排序。也就是利用判断矩阵计算各因素对目标层的权重。

（4）进行一致性检验。完成判断矩阵后计算出成对比较矩阵的特征向量。由特征向量求出最大特征根λmax。用最大特征根λmax和公式对比较矩阵进行一致性检验，当CR ＜ 0.1时，则认为判断矩阵具有满意的一致性。否则需要把判断矩阵表重新调整。

（5）最后进行层次总排序。计算底层元素对系统目标的合成权重进行总排序，总排序就是利用层次单排序结果计算各层次的组合权数，总排序的结果也就是各方案的优先次序。

2．实例分析

（1）层次结构模型建立。服装厂选址备选方案有两个，一共有五个影响因素，这五个因素之间关系用图2-7表示，这个也是得出的层次结构模型。

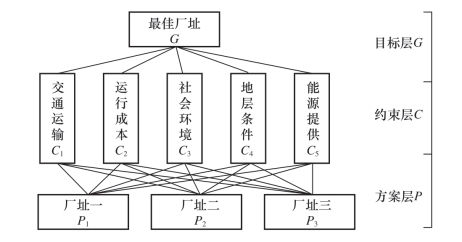
图2-7　某服装厂选址层次结构模型

（2）从上层要素开始，依次以上层要素为依据，对下一层要素两两比较，建立判断矩阵。根据层次结构图，本服装厂实例应建立两个层次的（A；B）共六个（A；B1；B2；B3；B4；B5）判断矩阵。约束层包含五个约束，交通运输C1，运行成本C2，社会环境C3，地层条件C4，能源供应C5。相对于目标层最佳厂址，进行两两比较打分。

（3）进行层次单排序。具体计算是：对于判断矩阵B，计算满足BW=λmaxW的特征根与特征向量。式中λmax为B的最大特征根，W为对应于λmax的正规化的特征向量，W的分量w即是相应元素单排序的权值。

具体计算方法如下：

按此方法计算得到A、B1、B2、B3、B4、B5判断矩阵与相应元素单排序的权值，见表2-4～表2-9：

表2-4　A 判断矩阵

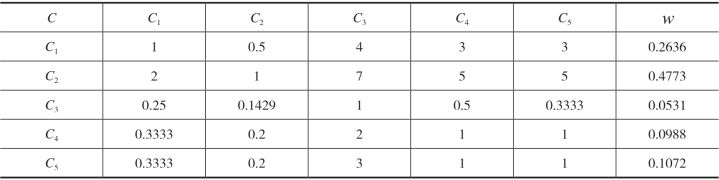
表2-5　B1 判断矩阵

表2-6　B2 判断矩阵

表2-7　B3 判断矩阵

表2-8　B4 判断矩阵

表2-9　B5 判断矩阵

（4）进行一致性检验。具体计算方法如下：

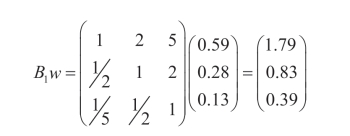
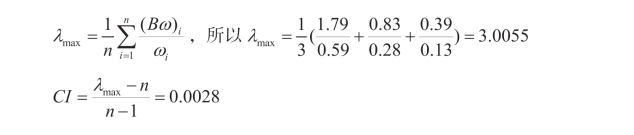
随机一致性指标RI：其值见表2-10。

表2-10　一致性指标RI 与n 的对照表

按此方法计算得到A、B1、B2、B3、B4、B5的CR分别为0.016、0.0053、0.0015、0.0000、0.0088、0.0000，都小于0.1，满足要求。

（5）最后的层次总排序。B1、B2、B3、B4、B5的五个特征向量构成一个矩阵与A的特征向量相乘，得到最终的排序向量W，见表2-11。

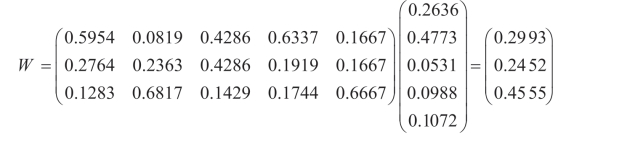
表2-11　最终权重表

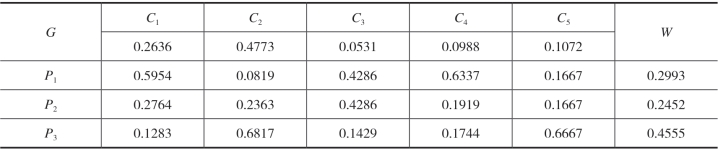
对总体优先级排序，可得P3＞P1＞P2。故厂址位置选择的最优方案为P3。因此，厂址3为最佳选址方案。