与囚徒困境博弈模型的静态博弈不同，动态博弈有两种类型，一种是重复博弈，即改变囚徒困境模型中一次性博弈的假定，使同样结构的博弈重复多次进行；另一种是序贯博弈，即考虑博弈主体的行动有先后顺序的情况，先行动者作出策略选择后，后行动者根据先行动者的选择所传递的信息调整自己的选择，先行动者也会意识到自己的行动会对后行动者传递有关信息而在选择策略时进行理性选择。考虑到劳动关系主体即雇主和雇员在现实策略选择中往往是相互作用的，这里利用序贯博弈模型对劳动关系主体的合作行为进行分析。

（1）薪资水平固定时雇佣双方的合作行为

在序贯博弈分析中，博弈树是主要的分析工具之一，是表示有限参与者进行有限策略动态博弈的一种树形图。博弈树可以清楚地表明博弈的行动先后顺序，并且能够给出有限博弈中包含的几乎所有信息。博弈树由结、枝和信息集组成，结包括决策结和终点结两部分，决策结代表博弈参与人及其采取行动的时点，终点结是博弈行动路径的终点，即各条博弈路径最终实现的不同博弈结果；枝是博弈树上从一个决策结到下一个结之间的连线，每个枝分别代表博弈主体所采取的行动策略；信息集是由博弈树上所有决策结分割成的不同行动策略及其实现的博弈结果。假设每一个参与博弈的主体所掌握的信息是充分且完备的，且都明确每一种博弈路径最终的结果，那么就可以剔除包含着不可置信的威胁策略，剩下的博弈路径将展现出实际可能会出现的均衡结果，“子博弈精炼纳什均衡”这个概念就是用来描述这一结果的。^[4]用博弈树表示的动态博弈也称扩展式博弈，而子博弈是扩展式博弈的一部分，是从一个单结信息集（只包括一个决策结的信息集）开始的与所有该决策结的后续结（包括终点结）组成的一个单独博弈。如果扩展式博弈的某个策略组合满足两个条件，一是这个策略组合是原博弈的纳什均衡，二是它在每一个博弈上也都构成纳什均衡，那么这个策略组合就是一个子博弈精炼纳什均衡。

科技型中小企业的雇主和雇员，可以利用序贯博弈对雇佣双方的动态博弈过程进行分析。考虑到科技型中小企业自身的特性，利用委托—代理理论能较好地阐明二者的相互关系。在这里，雇主是委托方，雇员是代理方，也就是被委托方，委托方的利益与被委托方的行为有密切关系。科技型中小企业的绩效主要取决于创新型人才的创新行为，其中以研发设计人才为主，同时也包括关键管理人才、生产人才和销售人才等。但是作为以脑力劳动为主的员工，企业很难直接控制其工作行为，对员工工作过程的监督也存在较大困难，只能通过报酬等形式间接影响员工的工作行为。由于科技型中小企业的研发和设计存在较高的不确定性，成功和失败的可能性并存，产品市场竞争力也容易受到技术和市场需求波动的冲击，因此，最终的绩效并不完全取决于代理方的工作情况，在这种情况下，监督问题就无法避免。但考虑到实施监督存在较大的难度，委托方必须思考用什么样的手段能够促使代理方的行为符合委托方的利益。雇主作为委托方可以利用的手段主要是委托合同的设计，而委托合同的核心条款主要是工资、奖金或利润分享等薪酬制度，因此委托-代理关系就表现为以薪酬为纽带的双方行为的博弈。

就科技型中小企业的雇佣双方而言，一方采取的行动或策略会直接影响另一方行为策略的选择，假定作为率先采取行动的一方主要采取薪酬策略，那么就可以利用委托-代理理论，通过扩展式博弈中的子博弈精炼纳什均衡分析雇佣双方的合作博弈行为。

为了研究的便利，假设科技型中小企业的产品价格和员工的工资水平都由市场决定，同时假定雇主首先决定给予雇员的薪资水平。考虑到企业经营可能会面临的风险，以及员工在工作过程中合作行为的选择，这里的薪资水平是相对固定的，暂时不考虑企业盈利后分享企业利润的问题，这样员工能够在行为选择之前有一个比较稳定的预期，此时雇主有两种选择：高薪资或低薪资。雇主选定策略后，雇员行为策略的选择同样有两种：高努力和低努力。据此，可以根据雇佣双方选定的不同策略绘制出如图6.4所示博弈树。

图6.4　雇佣双方序贯博弈树

图6.4中，雇主和雇员构成决策结；雇主下面的两个枝分别表示雇主的高薪资和低薪资两种策略，雇员下面的两个枝分别表示雇员的高努力和低努力两种策略；决策树的末端，即终点结代表四种不同的博弈结果，主要表现为雇主和雇员在不同博弈结果下各自的收益水平。

假设双方的博弈方式如下：雇主首先决定薪资水平，用W表示，构成企业投入的成本部分，并且是相对固定的，只要企业经营过程中没有遇到太大的风险，企业就需要按照事前的承诺支付给员工，薪资水平越高，企业支付的成本越多，这里暂且不考虑企业盈利水平提高后为员工分享利润的问题；雇员在得知雇主给定的薪资水平W后，根据W的高低选择努力程度E，努力程度越高，E越高，企业的绩效水平越高，因此E是W的函数，即E（W）。对于雇员来讲，W的提高有利于刺激雇员努力工作，从而提高E，但E的提高又会降低雇员的效用水平，即影响雇员工作之外其他需求的满足，因此，雇员总的效用水平U可以表示为W和E这两个变量的函数，即U＝U（W，E），其中，UW＞0，UE＜0。

假定企业在经营过程中单纯以利润最大化为追求目标，则企业的利润函数为：

π＝R（E）-C-W-T

式中，R为企业总收益，是员工努力程度E的函数，C为企业支付的除员工工资之外的其他固定成本和流动成本，T为企业缴纳的税费，设C和T均为常数，因此，这里的利润π为企业的净收益。假设企业总收益R是随着员工的努力程度E逐渐递增的，R（E）是严格递增的凹函数，即R′＞0，R″＜0。

这里首先求解在雇主给定薪资水平W的情况下，雇员的努力程度E。设E∗是雇员效用最大化时的努力程度，雇员效用最大化函数为：

MaxU（W，E）

上述函数的最优一阶条件为UW＋UEEW＝0，即由于UW＞0，UE＜0，因此EW＞0。(www.daowen.com)

上述结果意味着雇员实现效用最大化所需的努力程度E∗（W）是薪资水平W的递增函数。

从雇主的角度看，如果预期雇员将根据薪资水平W选择努力水平E，则在E∗（W）水平下，雇主实现利润最大化的函数为：

Maxπ（W，E∗（W））＝R（E∗（W））-C-W-T

上述函数的最优一阶条件为R′（E（W∗））EW-1＝0，将代入该式，可得：

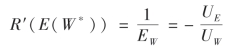
上式左边是雇主增加薪资水平对企业收益的边际影响，右边是雇员的边际替代率，即为了增加薪资的正效用而放弃的努力工作的负效用。从该式可知，雇主会选择薪资水平W∗，在W∗上实现企业利润最大化，子博弈精炼纳什均衡的结果是（W∗，E∗（W∗））。通过以上分析可知，在序贯博弈的情形下，由于雇主考虑到了薪资水平对雇员工作努力程度的影响，而雇员的工作努力程度又直接影响企业的收益水平，因此，雇主会通过提高雇员的薪资水平实现自身收益的最大化。相反，如果雇主降低薪资水平以减少企业成本支出，雇员通过降低努力程度减少工作带来的负效用，雇佣双方就很难达到共赢的目标，也不利于后续合作行为的实施，因此（W∗，E∗（W∗））很可能是一组雇佣双方的合作博弈解。

（2）实行利润分享后雇佣双方收益的变化与行为分析

以上分析重点考察了雇主和雇员中的一方选定策略后，对另一方行为选择造成的影响，通过序贯博弈分析，找出了双方可能的合作博弈解。但是上述扩展式博弈分析模型为了能够对雇员形成稳定的收入预期，假定企业支付的薪资水平是相对固定的。但是正如前文所分析的，对于科技型中小企业这种以创新为生命力的组织而言，人力资本价值含量较高的员工所占比重相对较高，且他们创新能力的发挥直接关系到企业的生存和发展。而人力资本产权的实现则直接体现为人力资本收益权的实现，这里的收益不仅包括较为稳定的基本薪酬部分，而且包含分享企业的部分利润。考虑到创新存在的风险，科技型中小企业在经营过程中面临的不确定性往往高于其他行业，即便是雇主选择了高薪资，雇员选择了高努力，最终结果仍然是成功和失败并存，对于研发和设计等岗位的员工尤为明显。以研发为例，假定在上述博弈树中，雇主选择了高薪资，雇员选择了高努力，最终结果包含成功和失败两种情况，那么形成的博弈树则如图6.5所示。

图6.5　包含结果的雇佣双方序贯博弈树

在上述博弈树中，假设成功的概率为P，失败的概率为1-P。如果成功，企业利润为π；如果失败，企业利润为π′。这里的π′是基于企业已有的资金、人才和技术成果，以及原有市场需求而产生的，且π＞π′。这样，企业的预期利润水平就可以表示为πP＋π′（1-P）。如果企业给员工支付的报酬仅包括预先承诺的基本薪资，则当研发成功时，雇员和雇主获得的收益组合为（W，π）；当研发失败时，雇员和雇主获得的收益组合为（W，π′）。当企业给员工支付的报酬除了基本薪资外，还包括企业部分利润时，双方的收益组合就会发生变化。假定企业给员工分享的利润比例为α，企业分享的比例为1-α，当研发成功时，雇员和雇主获得的收益组合为（W＋απ，（1-α）π）；当研发失败时，雇员和雇主获得的收益组合为（W＋απ′，（1-α）π′）。从短期角度看，实行利润分享后，雇员的收益增加，雇主的收益减少。在雇佣双方力量对比失衡的状态下，尤其是雇主力量强大的话，雇主是不会主动让雇员分享企业利润的。

然而，科技型中小企业的创新是一个长期的持续行为，即使创新失败，企业和员工也可以汲取经验和教训，进一步改进创新计划，在下一个创新周期取得进展和突破。因此，企业应该从双方长期合作的视角看待与员工的关系，注重长期激励机制的良好设计，实现企业的可持续发展。从调研结果的总体情况看，我国科技型中小企业所需的关键人才还是相对短缺的，而关键人才的流失无论是对处在起步和发展期的科技型中小企业，还是对已经进入成熟期的科技型中小企业，其损失都是致命的。对于人力资本价值含量较高的关键人才，其人力资本收益权无法充分实现往往成为流失的主要原因。上面的分析，只是从短期静态的视角分析了在员工没有获得利润分享权的情况下，员工和企业的收益情况，即当研发成功时，雇员和雇主获得的收益组合为（W，π）；当研发失败时，雇员和雇主获得的收益组合为（W，π′）。以上收益组合仅仅关注了当期双方的收益情况，如果员工因为没有分享企业部分利润而选择从企业离职，并且将离职成本也考虑进去的话，企业的收益就会出现一些变化。

这里需要考虑的一个主要因素就是重置成本。重置成本是指用一位能够在既定职位上提供同等服务的人员代替目前正在该职位上的人员时，必须付出的代价。重置成本包括员工的离职补偿费用、离职管理费用、离职前的效率损失、空职成本、新员工的招聘与培训费用等。对于科技型中小企业的核心人才，由于其培育周期较长，所花费的成本更高，离职后空缺的岗位即使在短期内得到了弥补，但新员工到岗后在短时间内很难达到原有员工的效率水平，由此造成的培训成本和效率损失均是重置成本的组成部分。尽管在会计核算时，这些成本要计入下一个或几个核算周期，但考虑到这些成本是由不恰当的长期激励机制引起的，同时出于研究问题的便利，这里将所有重置成本计入没有实行利润分享的这个研发周期内，并且用D表示。这样，在不实行利润分享的情况下，当研发成功时，雇员和雇主获得的收益组合为（W，π-D）；当研发失败时，雇员和雇主获得的收益组合为（W，π′-D）。如果将重置成本和利润分享加以考虑，雇主和雇员收益组合对比情况如表6.1所示。总体来看，将重置成本计入后，雇员的利益没有受到损失，雇主的收益有所减少。在此情形下，企业是否让员工分享企业的部分利润，关键是要对利润分享前后雇主的收益进行对比。

表6.1　雇员和雇主收益组合对比情况

从表6.1可知，实行利润分享后，研发成功和失败时雇主的收益分别为（1-α）π和（1-α）π′，经过整理后分别为π-απ和π-απ′，然后分别比较π-D和π-απ，以及π′-απ′和π′-D。当D＞απ和D＞απ′时，π-D＜π-απ，π′-D＜π-απ′；当D＜απ和D＜απ′时，π-D＞π-απ，π′-D＞π′-απ′。这里的απ和απ′分别表示研发成功和失败时员工可分享的利润水平。从这里的分析可以看出，不管研发成功还是失败，当关键人才流失造成的重置成本高于企业给员工分享的利润水平时，企业会选择让员工分享部分利润；反之，企业则不会让员工分享利润。对于科技型中小企业，关键人才在市场上的稀缺程度往往较高，其重置成本也相对较高，因此，帮助员工充分实现人力资本收益权是雇主和雇员双赢的选择，也是双方持续合作的动力所在。