下面给出了对零售商最有利的分离均衡（Separating Equilibrium）和混同均衡（Pooling Equilibrium）结果，而且，这两个均衡对其他均衡都是l-占优的，因此其他均衡不可能是词典顺序最大序贯均衡。

分离均衡：观测到不同需求信号的零售商收取不同的价格加成。引理5.1 给出了分离均衡结果，支持该均衡的制造商信念为：如果u≤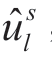，制造商认为零售商观测到的信号为sl；如果u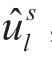＞，制造商认为零售商观测到的信号为sh。

引理 5.1 在没有信息共享情形下，对零售商来说，最有利的分离均衡为：l-类型的零售商选择价格加成为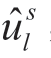 ，h-类型的零售商选择价格加成为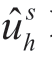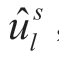＞，其中：

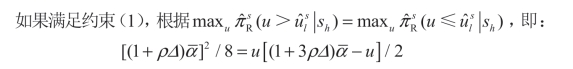
如图5.1 所示。

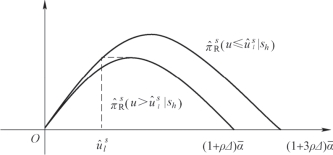
图5.1　激励相容约束（5.1）

即需要下面条件：

另外，对于h-类型零售商来说，根据：

可得其最优决策为：

根据下面条件：

可知l-类型零售商的最优决策为：

类似地，根据约束（1A.2），可得下面条件：

等式右边的值可以通过求解：

如图5.2 所示。

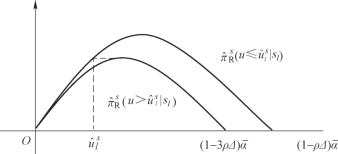
图5.2　激励相容约束（5.2）

然而，这个解存在需满足：

显然，上面不等式成立的条件为：(www.daowen.com)

根据引理5.1 中的分离均衡结果，零售商事先（观测到需求信号之前）的期望利润为：

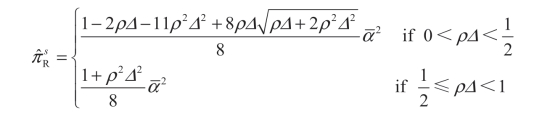
制造商事先的期望利润为：

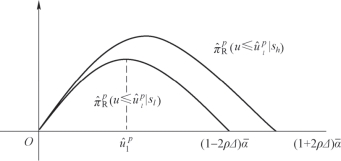
图5.3　约束（5.7）和（5.8）

根据引理 1.2 的混同均衡结果，零售商和制造商的事先期望利润为：

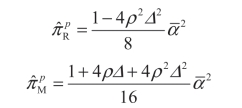
词典顺序最大序贯均衡（LMSE）。根据引理5.1 和5.2 的均衡结果，利用 LMSE 概念进一步对分离均衡和混同均衡进行筛选，结果见引理5.3。

定义τ1 ∈(0,2/13)且满足下面条件：

求解可得：

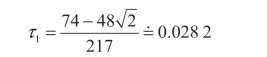
引理5.3 如果没有信息共享，存在唯一的LMSE 均衡，具体来说：

（a）如果ρΔ≤τ1，存在混同均衡，零售商最优加成为 u=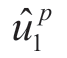=((1-2 ρΔ)/2) ；

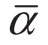（b）如果τ1＜ρΔ≤1，存在分离均衡，l-类型和 h-类型零售商的最优加成分别为：

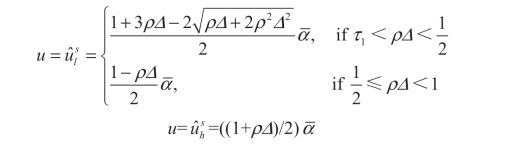
引理5.3 证明 在模型中，如果在所有的完美贝叶斯纳什均衡中l-类型零售商是获利最多的，而且基于此h-类型零售商也是获利最多的，那么该完美贝叶斯纳什均衡是LMSE 均衡。因此，为得到LMSE 均衡，需比较分离均衡和混同均衡下的l-类型零售商的期望利润。这些利润分别是：

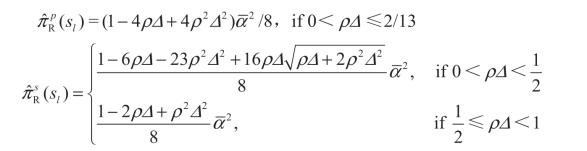
当 0＜ρΔ ≤2/13＜1/2，

其中：

通过比较引理5.3 中，零售商和制造商事先利润以及信息共享时的事先利润发现：当0＜ρΔ≤τ1 时，零售商倾向于信息共享，但这样会伤害到制造商和整个供应链；当τ1＜ρΔ≤1/2 时，零售商偏好分离均衡；当ρΔ＞1/2 时，分离均衡结果同信息共享时的结果一样。