类似批发价格合约，在模型满足一定限制性假设的前提下获得了信息不对称菜单合约中供应链决策的部分结果。因为菜单合约的复杂性，在进行模型推导时并没有获得完整形式的封闭解，因此不能仅通过理论结果得出此时信息精度对供应链决策的影响。在这种情况下，我们将使用 Fortran 软件采取更广泛的数值算例进行验证分析，对相关结论的可推广性和适用性进一步验证，并通过放开相关假设并考虑其他形式的需求分布（如正态分布等）来检验结论是否具有一般性。

与批发价格合约中的数值分析相比，在菜单合约中，将缩小参数间距，利用更为详细的数值算例进行相关结论的验证分析，令c=3.52，μ =10，其他参数的值设置如下：

ρ：依次从0.0～1.0 取值，间距为0.01；

γ ：依次从0.1～0.9 取值，间距为0.1；

表4.5　菜单合约下信息精度的影响（均匀分布）

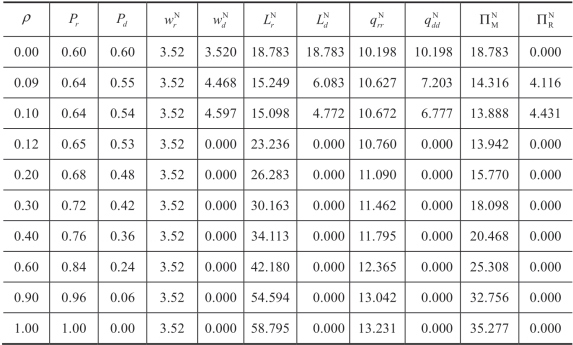
参数值： p=10.04，c=3.52，v=2.0，μ= 10.0，σ = 3.0，γ = 0.6，F 服从均匀分布。

表4.5 给出了 以及F 服从均匀分布的信息不对称情形下菜单合约供应链决策的数值结果。为了进一步验证结论，我们考虑了与引理3 不同的其他分布，表4.6 考虑了相同参数设置下正态分布的情况。

表4.6　菜单合约下信息精度的影响（正态分布）(www.daowen.com)

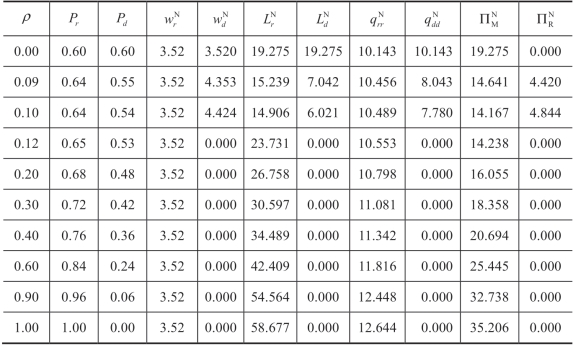
参数值： p=10.04，c=3.52，v=2.0，μ= 10.0，σ = 3.0，γ = 0.6，F 服从正态分布。

从表4.5 和表4.6 中，可以直观地看出以下几点：

（1）从表4.5 可以看出，存在一个临界点ρ（通过详细的数值分析可以得到临界点Nρ =0.106），当ρ ≤0.106 时，制造商设计的最优合约可以适用于 sr 型和 sd 型两种类型零售商，而当ρ ＞ 0.106 时，制造商将关闭低效的 sd 型零售商。

（2）当信息精度低于临界值Nρ 时，制造商的预期利润随着信息精度升高而降低；当信息精度超过临界值时，制造商利润随着信息精度的升高而升高，即制造商利润函数呈U 形变化。

（3）当信息精度低于临界值Nρ 时，零售商的预期利润随着信息精度的升高而升高；当信息精度超过临界值时，零售商的预期利润变为0；

（4）表4.5 和表4.6 中各个参数的变化趋势具有一致性，也就是说，即使当F 服从不同分布或者γ 不取特殊值时，我们得到的主要结论也是成立的，具有一般性。

本节主要介绍了信息不对称菜单合约中信息精度对供应链决策的影响。我们发现当信息精度ρ 很低时，制造商为了设计出适用两种类型零售商的合约保证供应链效率，菜单合约将被扭曲，以防止不同类型零售商之间发生伪装。这样的合约扭曲有利于零售商，但会造成制造商利益的损失，当信息精度ρ 逐渐增加时，合约扭曲程度将达到不可接受的水平。此时，不断增加的信息租金最终将迫使制造商关闭低效的 sd 型零售商，专注于与 sr 型零售商进行交易，制造商将从关闭策略中获益。因为制造商总能通过一次性支付 Lr 提取全部的渠道利润，而仅留给零售商保留利润。

通过对4.2 节中批发价格合约和本节菜单合约两部分决策结果的对比分析和数值验证，我们发现两种合约下的主要结果是一致的，没有因为合约选择的改变而改变主要结论。不同的是，在更为复杂的菜单合约下，我们没有完全获得封闭解，但是通过大量的数值算例从另一个角度佐证了结论，即，在两种合约中信息精度对供应链决策影响的根本原因是相似的。制造商总是在供应链效率和信息租金之间进行权衡，以便获得最佳合约。当付出较少信息租金可以保证供应链效率时，制造商会降低批发价以设计出适用两种类型零售商的合约；当信息租金付出较高时，制造商会采取关闭策略，仅与高效型 sr 型零售商进行交易，以保证自身利益。