4.2.2.1 批发价合约参照模型
为了便于信息不对称问题的分析,首先考虑一个简单的信息对称的批发价格合约。在这种情形下,制造商和零售商都只能获得关于市场状态先验分布的信息,即,零售商此时不能获得额外的信号信息以减轻其对市场状态预测的不确定性。在简单的批发价格合约下,零售商通过确定订购量q 对制造商提供的批发价w 做出响应。此时市场正常![]() 的先验概率是γ ,而市场中断
的先验概率是γ ,而市场中断![]() 的先验概率是1 - γ。对于给定的w,零售商的预期利润可以表示为:
的先验概率是1 - γ。对于给定的w,零售商的预期利润可以表示为:
![]()
其中,![]() 表示零售商预测在市场状态正常的情况下未能销售的产品数量。零售商在上述公式中确定最优订购量以实现自身利益最大化的问题等价于缺货成本为p -w/ γ和过剩成本为 w/γ -v 的经典报童模型问题。
表示零售商预测在市场状态正常的情况下未能销售的产品数量。零售商在上述公式中确定最优订购量以实现自身利益最大化的问题等价于缺货成本为p -w/ γ和过剩成本为 w/γ -v 的经典报童模型问题。
零售商的最优订购量可以表示为:
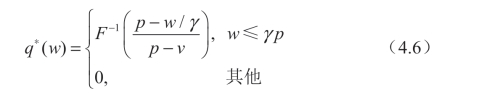
相应地,零售商和制造商的预期利润为:
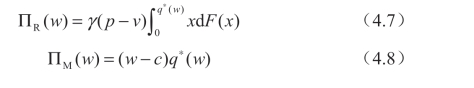
从公式(4.6)中可以得到:

制造商的最优批发价格w为:
![]()
上述式子中 g ( q) 定义为分布F 一般失效率:
![]()
引理4.1 的具体证明见附录A4.2。
对于供应链垂直整合的情况,制造商可以看作下游零售商,由此可知,预期渠道利润和订单数量随着市场中断概率的增加而降低。对于批发价格合约下分散决策的情况,产品订购量依然随着中断概率增加而下降,整个供应链渠道也会因为双重边际化和中断风险变得更糟。
4.2.2.2 问题描述和决策顺序
本节首先考虑信息不对称下批发价格合约[ w] 中的决策情况。在这种合约下,制造商仅能制定一个恒定不变的批发价格w 提供给零售商。为了研究信息不对称下的决策情况,批发价格合约模型在基本模型的第一步中零售商已经决定不与制造商分享其私人信息 sm 。根据基本模型,批发价格合约模型下事件的决策顺序(如图4.2 所示)按以下步骤进行。
首先,零售商观测到关于市场状态的信号 sr 或 sd ,其信息精度为ρ,这是零售商的私有信息。在此之前零售商已经决定不与制造商分享信息,相对制造商而言,零售商占据了信息优势。

图4.2 批发价格合约模型下事件的决策顺序
其次,制造商根据对市场判断的先验知识和预测零售商收到的市场信号,向零售商提供批发价格合约{w } ,即确定每个产品的批发价格w。
然后,零售商根据观测到的市场信号更新其原有的对市场判断的先验知识,并以自身利益最大化为目标向制造商确定产品订购量并支付wq 的对价。
最后,市场需求不确定消失,真实的市场状态发生。如果市场状态是正常的,零售商的行为则会遵循传统的报童模型,如果市场状态是中断的,零售商订购的全部库存都将失去价值。
只有在信息精度ρ <1 的情况下,零售商对于市场状态的预测才不是完全准确的,即,即使零售商观测到的信号是市场中断信号 sd ,真实的市场状态也可能是正常的。在这种情况下,零售商依然可能确定产品订购量q>0 。
4.2.2.3 批发价格合约模型及决策结果
针对上述研究问题和相关假设,可以构建出制造商和零售商的最优利润函数模型。其中,将以最大化制造商预期利润作为目标函数,零售商最优订购量为约束条件,因此,在信息不对称的情形下,批发价格合约供应链决策问题可以用下述模型表示:
![]()
约束条件为:
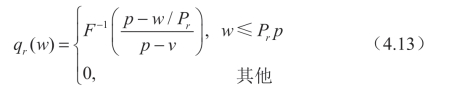

为了便于数学上的处理,假设市场需求![]() ,并假设先验概率γ =1/2。因为当p≤2c 时会导致退化情况的出现,即制造商将会只与 sr 类型的零售商进行交易,所以假设p>2c 。基于以上假设,我们通过逆向归纳法求解了批发价格合约模型,并在引理4.2 中总结了在信息不对称的情形下,制造商和零售商在批发价格合约中的最优决策结果。
,并假设先验概率γ =1/2。因为当p≤2c 时会导致退化情况的出现,即制造商将会只与 sr 类型的零售商进行交易,所以假设p>2c 。基于以上假设,我们通过逆向归纳法求解了批发价格合约模型,并在引理4.2 中总结了在信息不对称的情形下,制造商和零售商在批发价格合约中的最优决策结果。
引理 4.2 如果分布函数F 是区间[0,1]上的均匀分布,γ =1/2且p>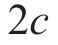 ,制造商和零售商的最优决策结果可以表示为:
,制造商和零售商的最优决策结果可以表示为:
当ρ ≤ρN 时 :

相应的制造商和零售商的最大利润分别为:此时制造商和零售商的最大利润为:(https://www.daowen.com)

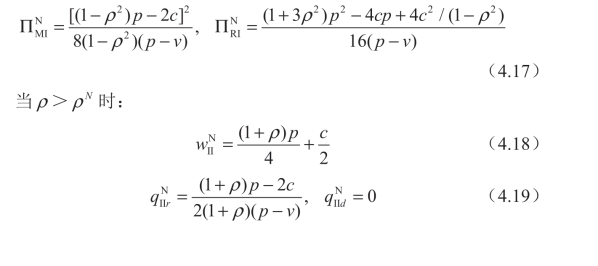
其中:

接下来进一步将制造商和零售商的预期利润是怎样被信息精度ρ影响的结果汇总在命题4.1 中。详细的证明过程见附录A4.4。
命题 4.1 如果分布函数F 是区间[0,1]上的均匀分布,γ =1/2且p>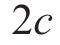 ,则制造商的预期利润是随着信息精度ρ 变化的拟凸型函数,即U 形,而零售商的预期利润是随着信息精度ρ 变化的分段递增函数。
,则制造商的预期利润是随着信息精度ρ 变化的拟凸型函数,即U 形,而零售商的预期利润是随着信息精度ρ 变化的分段递增函数。
直观地说,随着信息精度ρ 逐渐增加,零售商即使在接收到信号后不能完全确定市场状态,对制造商的信息优势也会增加,因此,零售商通过与制造商的交易应该赚取更多的收益,制造商由于加剧的信息劣势应该会变得更糟,然而,命题4.1 的结果似乎有些违反直觉。经过分析,将命题4.1 中违反直觉的结果解释如下:
(1)当信息精度ρ 相对较低,即![]() 时,信息不对称程度低,制造商为了设计出适用于
时,信息不对称程度低,制造商为了设计出适用于 和
和 两种类型零售商的合约,因此提供的合约将被扭曲,即降低批发价w。在这种情况下,由于零售商的信息优势不太明显,制造商在不需要付出太多信息租金的前提下,便可以削弱供应链双重边际效应,从而提高整个渠道的效率。制造商以牺牲一部分自身利益为代价改善了供应链效率,在这种情况下,结果是符合直觉的,即,制造商的情况会随着信息精度的增加而变得更糟糕,而零售商从他的信息优势中受益更多。
两种类型零售商的合约,因此提供的合约将被扭曲,即降低批发价w。在这种情况下,由于零售商的信息优势不太明显,制造商在不需要付出太多信息租金的前提下,便可以削弱供应链双重边际效应,从而提高整个渠道的效率。制造商以牺牲一部分自身利益为代价改善了供应链效率,在这种情况下,结果是符合直觉的,即,制造商的情况会随着信息精度的增加而变得更糟糕,而零售商从他的信息优势中受益更多。
(2)当![]() 时,制造商则会因合约扭曲需要支付的信息租金变得太高决定关闭低效的 sd型零售商,不再为其提供合约。由于零售商预测信息的信息精度越来越高,因此,此时制造商只与高效的 sr型零售商交易并且收取更高的批发价格(即
时,制造商则会因合约扭曲需要支付的信息租金变得太高决定关闭低效的 sd型零售商,不再为其提供合约。由于零售商预测信息的信息精度越来越高,因此,此时制造商只与高效的 sr型零售商交易并且收取更高的批发价格(即 ),而零售商由于信息精度的提高会更加确信市场状态,所以更高的批发价不会阻碍其订购更多的产品,即,批发价
),而零售商由于信息精度的提高会更加确信市场状态,所以更高的批发价不会阻碍其订购更多的产品,即,批发价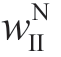 和订购量
和订购量 都随着信息精度ρ 增加而增加(即
都随着信息精度ρ 增加而增加(即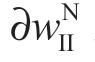 /
/![]() 此时制造商和零售商都将从这个关闭策略中受益。
此时制造商和零售商都将从这个关闭策略中受益。
4.2.2.4 数值算例
上述信息不对称批发价格合约模型中得到的相关结论是在满足一些限制性假设的前提下获得的,即需求分布F 满足区间[0,1]上均匀分布,先验概率γ =1/2。这种假设是为了便于我们在数学上进行处理,尽管在理论研究中很常见,但是供应链模型和真实情况依然存在很大的差距,其结论的可推广性和适用性需要进一步检验,因此,将在本节中放开相关假设,并考虑其他形式的需求分布(如正态分布等)来检验得到的结论是否可以推广,是否具有一般性和适用性。
接下来,进一步探讨当F 为其他分布或者γ 取不同值时的相关结果,然而,当F 遵循不同于命题4.1 中的分布或者γ 不取值为1/2 时,难以像引理4.2 和命题4.1 中那样获得制造商和零售商利益最大化问题的封闭形式解,因此,我们使用 Fortran 软件进行了多种参数组合的数值算例分析,并验证了本节得到的主要结论。
令c=3.52 和μ =10。其他参数的值设置如下:
ρ:依次从0.0~1.0 取值,间距为0.1(也就是说一共有11 个不同的值);
γ :依次从0.1~0.9 取值,间距为0.1(也就是说一共有9 个不同的值);
σ :依次从1.75~4.25 取值,间距为0.25(也就是说一共11 个不同的值);
p:![]() 依次从2.1~5.9 取值,间距为0.2(即一共20 个不同的值。因为
依次从2.1~5.9 取值,间距为0.2(即一共20 个不同的值。因为![]() 时会导致退化情形的产生,所以仅考虑k > 2的取值情况)。
时会导致退化情形的产生,所以仅考虑k > 2的取值情况)。
因此,考虑总体为11×9×11×20=21 780 条记录的测试问题,所有得到的数值算例结果都支持命题4.1 中的主要结论。
在此基础上,选取参数分别为p=10.04,c=3.52,v=2,μ =10,σ =3 和γ =0.6,并且F 服从均匀分布或正态分布的数值结果作为代表性算例给出。具体结果见表4.2 和表4.3。
表4.2 批发价格合约下信息精度的影响(均匀分布)

续表
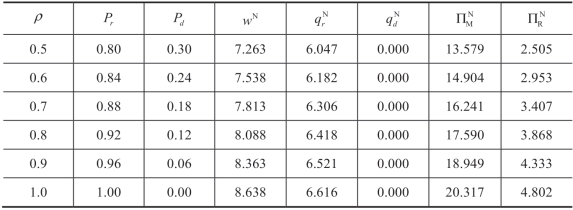
参数值: p=10.04,c=3.52,v=2.0,μ= 10.0,σ = 3.0,γ = 0.6,F 服从均匀分布。
表4.2 给出了μ =10,σ =3,γ =0.6 以及F 服从均匀分布的信息不对称情形下批发价格合约供应链决策的数值结果。
为了进一步验证我们得到的结论,表4.3 中的参数数值采取了与表4.2 相同的设置,区别则是假设此时的市场需求分布满足正态分布,目的是研究信息精度对供应链决策的影响是否会因为不同需求分布而发生改变。
表4.3 批发价格合约下信息精度的影响(正态分布)
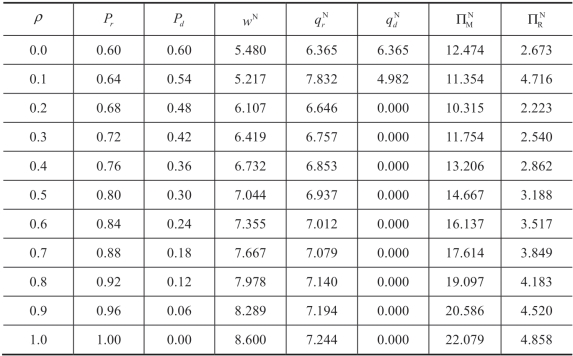
参数值: p=10.04,c=3.52,v=2.0,μ= 10.0,σ = 3.0,γ = 0.6,F 服从正态分布。
从表4.2 和表4.3 中可以直接看出以下几点:
(1)表4.2 显示,当预测信号的信息精度ρ 低于临界点(通过更为详细的数值分析,可以得出本算例中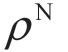 =0.156)时,制造商收取的批发价格w 足够低,条件概率 Pd 相对较高,这使得零售商即使在观察到信号 sd 的情况下依然愿意下单, qd > 0。
=0.156)时,制造商收取的批发价格w 足够低,条件概率 Pd 相对较高,这使得零售商即使在观察到信号 sd 的情况下依然愿意下单, qd > 0。
(2)当信息精度![]() 时 ,制造商的批发价
时 ,制造商的批发价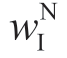 逐渐降低,
逐渐降低, 和
和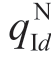 都大于0,也就是说此时零售商不论收到何种信号类型都会订购产品。然而,当
都大于0,也就是说此时零售商不论收到何种信号类型都会订购产品。然而,当![]() 时,只有当
时,只有当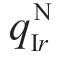 大于0 时,即,此时零售商仅在观察到的信号为 sr时会订购产品。
大于0 时,即,此时零售商仅在观察到的信号为 sr时会订购产品。
(3)随着信息精度ρ 的逐渐升高,制造商的预期利润呈现先减后增的趋势,而零售商的预期利润是在临界点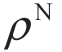 处突然下降,而在其前后呈现分段递增的趋势。
处突然下降,而在其前后呈现分段递增的趋势。
(4)表4.2 均匀分布和表4.3 正态分布的数值结果中各个参数的变化趋势具有一致性。研究表明,即使当F 服从不同分布或者γ 不取特殊值时,之前得到的主要结论也是成立的,数值算例进一步验证了结论的一般性。
在本节的内容中,首先对全文研究的供应链问题、假设和基本模型等进行了介绍。针对本文研究的主要内容,首先提出了基本模型,便于后续节中不同合约以及信息共享与否情况下的决策模型构建和进一步分析;同时,本节首先选择了较为常见和使用的批发价格合约,对其在信息不对称下信息精度对供应链决策的影响进行了研究。
在信息不对称下的批发价格合约供应链决策中,通过理论结果的推导和数值算例的对比验证,分析了制造商的批发价格、零售商最优订购量以及制造商和零售商的利润变化,发现了一些与直觉相反的一些结果。在信息不对称的情况下,零售商因为具有私人市场预测信息相对于制造商产生了信息优势,直觉上,我们认为制造商的利润会随着零售商的信息优势的扩大(也就是信息精度升高)而变得更糟,而零售商的利润会变得更好;然而,得到的结论表明,制造商的利润不是信息精度的单调减函数,即,制造商的利润不会因为扩大的信息劣势而变得更糟。相反,随着信息精度的逐渐升高,直到超过某个临界值时,制造商和零售商的利润都会随着信息精度的升高而升高,即,此时两者都从信息精度的提高中受益。针对上述结论,本节给出了相关的解释和验证。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。







